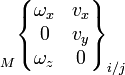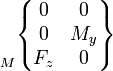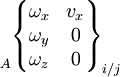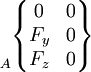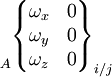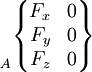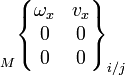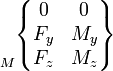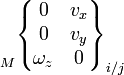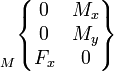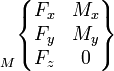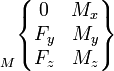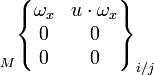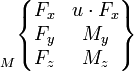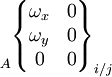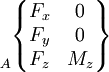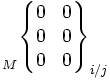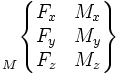- Pivot (mecanique)
-
Liaison (mécanique)
 Pour les articles homonymes, voir liaison.
Pour les articles homonymes, voir liaison.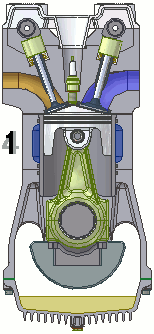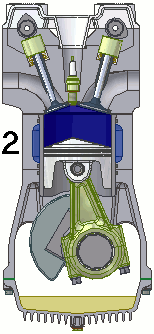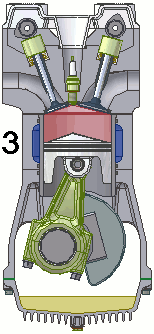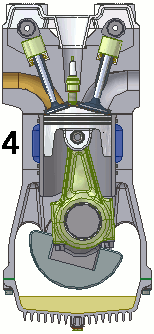 les Liaisons piston/bielle et piston/chemise sont des pivots glissants
les Liaisons piston/bielle et piston/chemise sont des pivots glissantsUn mécanisme est l'association de plusieurs pièces liées entre elles par des contacts physiques qui les rendent totalement ou partiellement solidaires, selon qu'ils autorisent ou non des mouvements relatifs. La liaison mécanique est le modèle utilisé pour décrire cette relation dont la considération est primordiale dans l'étude des mécanismes. Elle emploie des représentations mathématiques qui diffèrent suivant qu'on l'aborde sous l'aspect cinématique (étude des mouvements ou guidages) ou sous l'aspect statique (étude de la transmission d'efforts).
La notion de liaison mécanique se définit plus généralement entre groupes de pièces, appelés classes d'équivalence contenant respectivement des pièces entièrement solidaires.
A partir de l'analyse des surfaces de contact entre deux solides, et en considérant des surfaces usuelles, on établit une nomenclature proposant 12 liaisons normalisées depuis la liaison nulle qui n'a aucun effet jusqu'à la liaison complète qui solidarise les deux pièces.
Certains dispositifs mécaniques, s'interposant comme un joint entre deux éléments peuvent être considérés comme liaison directe[1] entre ces éléments. C'est la cas du joint de Cardan établissant l'équivalent d'une liaison rotule à doigt entre deux arbres, ou de l'association de deux roulements à billes liant par un pivot un arbre et son logement.
Sommaire
Classification des liaisons élémentaires parfaites
Une liaison mécanique entre deux pièces existe s'il y a contact direct entre une ou plusieurs surfaces respectives de ces pièces. Il en résulte un ensemble de points de contact; ces points peuvent êtres isolés dans l'espace, disposés sur une ligne commune ou répartis sur une surface.
Pour être complète, l'analyse doit de plus considérer la direction de la normale de contact en chaque point. On montre alors que le nature de la liaison est entièrement liée à la répartition spatiale des ces normales de contact.
En combinant des surfaces de forme simple[2], on construit une liste de cas correspondant à des liaisons élémentaires, donnant les bases pour l'établissement des modèles de calcul en mécanique.
La liste présentée commencera par les liaisons les moins contraignantes pour finir sur les liaisons les plus complètes. Les 10 liaisons élémentaires proposées, auxquelles il faut rajouter la liaison nulle et la liaison complète, constituent l’ensemble des liaisons mécaniques élémentaires[3] rencontrées dans un mécanisme.
Pour ce faire, la géométrie des surfaces considérées est supposée toujours parfaite[4], les assemblages sans jeu, et les contacts permanents et sans frottement, c'est-à-dire sans résistance au glissement.
Pour chaque liaison, on proposera :
- un (ou plusieurs) exemple théorique combinant les surfaces simples permettant la réalisation du contact.
- un tableau donnant :
- la dénomination normalisée de la liaison, avec sa référence centrée (permettant la construction du repère local avec directions principales par lequel sont distingué les degrés de liaison ou de liberté.
- une représentation schématique (selon la norme), en vue plane et spatiale,
- les degrés de liaisons et les degrés de liberté.
- des cas réels modélisables par une telle liaison.
Le repère local proposé sur les schémas est volontairement donné incomplet pour mieux mettre en valeur les points et directions intrinsèques à la liaison (première direction X, deuxième Y, etc.) Le schéma associé à chaque liaison est proposé en deux couleurs représentant respectivement une des pièces en jeu.
Les liaisons simples
Une liaison mécanique simple, est une liaison obtenue par un contact entre une surface simple unique d'une pièce avec celle, simple et aussi unique d'une autre pièce. En se limitant au cas des plans, cylindre et sphères, on obtient l'ensemble des cas ci-dessous.
Liaison ponctuelle
La liaison ponctuelle décrit un contact entre deux solides qui se réduit à un point. Par obstacle, ce contact interdit le rapprochement des deux corps, et autorise la transmission d'une force dans la direction normale (perpendiculaire) au plan tangent commun aux deux surfaces en contact. On définit ainsi son seul degré de liaison.
La translation perpendiculaire au plan tangent du contact est contrainte. Les glissements dans le plan tangent et les rotations sont libres. De ce fait, la normale de contact constitue l'axe principal de la liaison. La définition d'une liaison ponctuelle doit préciser la localisation du point de contact et la direction de sa normale.
En réalité, une liaison n'est jamais strictement ponctuelle. En effet la pression au point de contact serait infinie, conduisant les solides à se déformer et la zone de contact à s’élargir. Mais tant que cette surface reste très petite devant les dimensions de l'objet, il est raisonnable de considérer que la liaison est ponctuelle (d'un point de vue macroscopique). Ainsi l'appui d'un pied de chaise peut être modélisé par une liaison ponctuelle.
Sur les deux premiers exemples proposés, la liaison est dite unilatérale: en effet, si un tel contact interdit le rapprochement des corps, il ne s'oppose pas à leur écartement. En règle générale, la modélisation mathématique d'une liaison considère un comportement bilatéral. Si cette propriété est nécessaire pour un mécanisme réel, cela ne peut s'obtenir que par l'association d'une autre ponctuelle de même normale mais de sens opposé (par exemple une sphère prise en sandwich entre deux plans solidaires et diamétralement opposés). Cette propriété est parfois plus importante sur d'autres liaisons comme l'appui la glissière ou le pivot glissant.
Ponctuelle
en A
de normale Z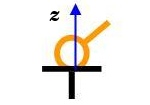
non normalisée
Liaisons :
Tz = 0Libertés :
Tx, Ty
Rx, Ry, RzC’est la liaison génératrice de toutes les autres, puisqu’une liaison peut toujours être décrite par plusieurs liaisons ponctuelles, qu'il s'agisse d'un ensemble discret ou continu de points. Dès lors qu'une association de points de contact dispose des mêmes particularités géométriques, elle constitue une seule et même liaison mécanique.
Lorsque deux pièces sont liées par une ponctuelle, il existe un point fixe d'une des pièces coïncidant avec une surface fixe de l'autre. Il ne s'agit pas forcément du point de contact ou des surfaces en contact. Dans le cas d'une sphère en contact sur un cylindre, ce point est le centre de la sphère et la surface un cylindre coaxial de rayon égal à la somme des rayons des deux surfaces de contact.
Liaison linéaire rectiligne
Cette liaison est obtenue lorsqu'elle présente un ensemble de points de contact alignés dont les normales sont toutes parallèles. Idéalement elle est l'association de 2 ponctuelles.
Elle présente 2 degrés de liaison : la translation perpendiculaire au plan tangent (soit suivant la direction des normales) et toute rotation d'axe perpendiculaire au plan des normales de contact.
Cette liaison, malgré sa simplicité est sans doute la plus tridimensionnelle de toutes, son comportement étant différent dans les 3 directions de l'espace. Sa définition complète doit donc préciser le plan contenant la ligne des points de contact et la direction commune des normales de contact.
De même que pour le contact ponctuel, le contact suivant une ligne (d'épaisseur nulle) est improbable. Il y a déformation sous la pression. On pourra assimiler une surface rectangulaire peu large à une ligne de contact: Un rouleau sur son support ou une plaque posée sur chants, sont des cas de liaison linéaire rectiligne.
Dans ce cas aussi, on aboutit le plus souvent à une liaison réelle unilatérale. Un pion ajusté et coulissant dans une rainure oblongue constitue cependant une solution bilatérale. Les deux lignes de contact sont parallèles et dans un plan contenant aussi l'ensemble des normales de contact.
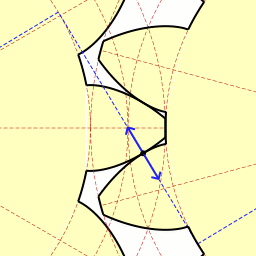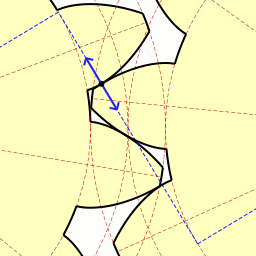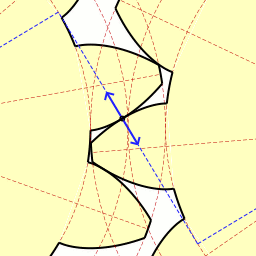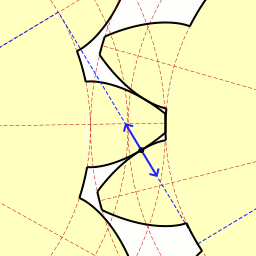
Dans un engrenage droit[5], la liaison entre deux roues peut être modélisée par une linéaire rectiligne si l'épaisseur des pignons n'est pas négligeable.
Linéaire rectiligne
de ligne (A,x)
de normale Z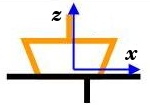

Liaisons :
Tz = 0
Ry = 0Libertés :
Tx, Ty
Rx, RzLorsque deux pièces sont liées par une rectiligne, il existe deux points fixes d'une des pièces qui coïncident avec une surface fixe de l'autre.
Liaison linéaire annulaire
La liaison linéaire annulaire est obtenue lorsque le contact est réparti suivant un ensemble de points coplanaires et dont les normales de contact concourent. Cet ensemble est un cercle si on dispose une sphère dans un cylindre de même diamètre. Alors les normales de contact se rencontrent au centre de la sphère qui se confond avec le cercle des points de contact.
Cette liaison s'oppose aux deux translations transversales (radiales par rapport au cylindre de l'exemple). Tous les autres mouvements sont libres. La définition complète de cette liaison doit préciser la position du centre et la direction de la ligne suivie par ce centre. Dans certains cas, cette direction peut être variable, comme sur l'exemple ci-dessous où la goulotte contenant la bille change de direction. D'où l'importance de la considération d'un repère local.
On obtient un équivalent en disposant deux ponctuelles aux normales concourantes, par exemple un même sphère en contact sur deux plans solidaires et sécants.
En pratique, un jeu est nécessaire pour permettre l'assemblage de deux pièces. Dans le cas représenté d’une barre traversant une plaque, ce jeu autorise un débattement sensible, donc n'offre aucune résistance dans ces directions: la modélisation par une liaison annulaire est admise. On parle alors de centrage court. On admet ce modèle lorsque la longueur de l'assemblage (partie cylindrique commune) est très petite devant le diamètre ajusté. C’est ainsi la configuration obtenue au début de la pose d’un couvercle d’une casserole quand il se centre sur le bord intérieur de la casserole et qu'il peut encore pivoter dans tous les sens.
Une sphère dans un cylindre (non rectiligne): cet exemple justifie le nom gouttière parfois attribué à ce cas.
Linéaire annulaire
de centre A
et d'axe (A,x)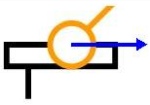
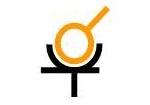
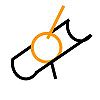
Liaisons :
Ty = 0
Tz = 0Libertés :
Tx
Rx, Ry, RzLorsque deux pièces sont liées par une annulaire, il existe un point fixe d'une des pièces coïncident avec une courbe fixe de l'autre. On appelle aussi cette liaison ainsi : point sur courbe..
Liaison rotule
La liaison rotule s'identifie facilement par ses degrés de libertés: elle lie complètement deux pièces en translation mais les laisse libres en rotation. Elle comporte donc 3 degrés de liaisons (les 3 translations) et 3 degrés de liberté (les 3 rotations).
Elle est l'association de ponctuelles non coplanaires dont les normales concourent en un même point qui constitue le centre de cette liaison. Le cas le plus simple est celui de deux sphères mâle et femelle. La définition de cette liaison doit préciser la position de son centre. Aucune direction n'est privilégiée du point de vue du comportement.
En pratique, une des directions de rotation au moins est limitée par la présence d'ancrages mécaniques.
On trouve cette liaison dans les attelages de caravane qui assurent un découplage en roulis, tangage et lacet. Dans ce cas particulier, les deux premières rotations sont limitées par l'attelage ; la troisième l'est par obstacle de la remorque sur le véhicule tracteur.
On les trouve à l'extrémité des biellettes, pour leur permettre de grandes angulations, ou des barres pour les protéger des charges en flexion ou en torsion. Des fabricants proposent des éléments standard qui s'interposent facilement.
Certains roulements rigides à une rangée de billes constituent également une liaison rotule[6]. De ce fait, il faut toujours deux roulements pour réaliser une liaison pivot.
Association cône/sphère. L'ensemble des points de contact est une cercle mais les normales ne sont pas coplanaires.
Rotule
de centre A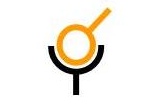

Liaisons :
Tx = 0
Ty = 0
Tz = 0Libertés :
Rx, Ry, RzIl n'existe qu'une seule vue de représentation schématique, dans la mesure où aucune direction ne se distingue.
Lorsque deux pièces sont liées par une rotule, il existe un point fixe d'une pièce coïncidant avec un point fixe de l'autre. Ce point est le centre de la liaison.
L'articulation du genou n'est pas proprement dit une rotule.
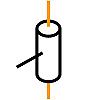
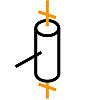
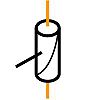
Liaison pivot glissant
Elle s'obtient lorsque tous les points de contact appartiennent à un ou plusieurs cylindres coaxiaux. Les normales de contact rencontrent toutes l’axe de ces cylindres qui devient naturellement l’axe de la liaison. C’est la seule direction caractéristique.
Les leviers de vitesse des 2CV et des 4L sont liés à la planche de bord par un pivot glissant.
Cette liaison se comporte comme deux liaisons linéaires annulaires. Elle dispose de 4 degrés de liaison puisqu'elle lie les deux translations et les deux rotations transversales. Les degrés de liberté sont la translation et la rotation axiale.
Si la rotation peut facilement présenter une amplitude infinie (au moins un tour), la translation se limite aux dimensions des pièces. Cependant, dans le domaine de fonctionnement observé, la modélisation est maintenue.
La définition complète de cette liaison doit préciser la position de l'axe. S'agissant d'une droite, elle n'est complète que si on précise 2 points lui appartenant, ou un point et une direction. Cette direction est d'ailleurs la seule qui se distingue.
Les lignes de figurines d'un Babyfoot sont liées à la table par un pivot glissant.
Pivot glissant
d'axe (A,x)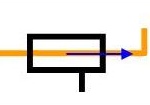

Liaisons :
Ty = 0
Tz = 0
Ry = 0
Rz = 0Libertés :
Tx
RxPar opposition à la linéaire annulaire, cette liaison nécessite un centrage long. La distinction technologique entre les deux se fait sur le rapport entre Rayon et Longueur de portée (assemblage cylindrique):
- Si L < R on acceptera la modélisation par une annulaire. Le jeu autorise un grand débattement angulaire.
- Si L > 2R le modèle pivot glissant s’impose. Un même jeu radial rend le débattement angulaire négligeable.
- Entre les deux, c’est au mécanicien de faire un choix, qui sera motivé par les résultats attendus. Dans le cas d'une étude statique, on préfèrera le modèle moins contraignant apportant moins d'inconnues. Dans le cas d'une étude cinématique, on préfèrera la liaison plus contraignante apportant plus d'équations pour résoudre le problème.
Cette liaison est très courante dans les mécanismes, où on la confond parfois avec la glissière. Elle est cependant moins contraignante à réaliser. On citera comme exemple la liaison entre piston et chemise, et, toujours dans le moteur à explosion, entre piston et bielle (même si, là encore, on pourrait croire à une liaison pivot). Dans les deux cas, le choix d’une liaison moins contrainte permet un positionnement naturel des pièces. .
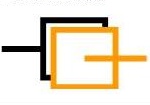
Liaison appui plan
La liaison appui plan, appelée aussi liaison plane, présente 3 degrés de liaison. Ils forcent le mouvement à rester dans un plan. Les deux translations et la rotation dans ce plan sont libres.
Cette liaison s'obtient naturellement en plaquant deux surfaces planes l'une sur l'autre. Plus généralement, il suffit que le contact entre deux solides s'effectue en au moins 3 points non alignés (et pas obligatoirement coplanaires) et de normales de même direction. Elle constitue la base des liaisons dites prismatiques. La direction commune des normales aux contacts élémentaires donne la direction principale de la liaison.
L'appui des trois pieds d’un tabouret sur un sol plan constitue une liaison plane. Le quatrième pied d’une chaise ne touche le sol que si les extrémités des pieds sont parfaitement coplanaires ; le système est alors hyperstatique les liaisons étant en surnombre par rapport au besoin de guidage.
Appui plan
de normale Z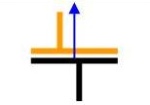
non normalisée
Liaisons :
Tz = 0
Rx = 0
Ry = 0Libertés :
Tx, Ty
RzLes points de contact ne sont pas nécessairement dans un même plan. Par exemple si on raccourcit une patte d'une chaise, on peut la placer dans un escalier, la patte la plus courte reposant sur une marche supérieure. Les normales étant parallèles, l'ensemble constitue toujours une liaison plane.
Lorsque deux solides sont en appui plan, il existe au moins un plan de l'un en coïncidence avec un plan de l'autre.
Liaisons composées
Les liaisons composées ne peuvent être obtenues qu’à partir d’association de surfaces multiples. De ce fait, il est possible de les modéliser par assemblage de liaisons simples. Le concepteur a souvent recours à ce concept pour définir les pièces participant à une liaison.
On pourrait donc arrêter là, la liste des liaisons élémentaires mais cela n’est pas justifié dans la mesure où pivot, glissière et hélicoïdale sont incontestablement les liaisons les plus employées dans les systèmes et font donc partie des liaisons mécaniques élémentaires de premier plan.
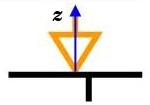
Liaison pivot
La liaison pivot est assurément la plus rencontrée dans les systèmes mécaniques. Elle guide en rotation une pièce en ne permettant qu'une rotation autour de l'axe de la liaison.
La définition de cette liaison doit préciser la position de son axe, c'est-à-dire d'une droite comme pour le pivot glissant. En effet pour une porte, de la position des gonds dépend le sens d'ouverture; de même un hayon de voiture est guidé par un pivot de direction horizontale placé en haut. S'il était en bas on obtiendrait une porte fourragère. La seule précision de la direction est donc insuffisante.
Les réalisations les plus courantes sont basées sur le complément d’un contact cylindrique par un arrêt axial : il s’agit souvent d’un plan normal à l’axe (pivot glissant + appui plan:solution hyperstatique); dans ce cas on distingue les pivots à cylindre prépondérant (cas d’une liaison de roue par palier lisse comme sur brouette) ou plan prépondérant (cas d’un couvercle). L'idéal étant l'association d'un pivot glissant avec une liaison ponctuelle.
Cette liaison peut être aussi obtenue par la combinaison d'une liaison linéaire annulaire et d'une rotule; un schéma que l'on retrouve dans certains guidages par roulements à billes.
Dans le cas des liaisons pivot, en particulier en ce qui concerne le blocage de la translation axiale, on distingue les liaisons unilatérales des liaisons bilatérales, suivant que ce degré de liberté est supprimé dans un ou deux sens. Si pour une porte la solution unilatérale[7] est suffisante, il est nécessaire de maintenir la roue d’un véhicule dans les deux sens. Cette approche est, bien sûr, technologique et ne concerne pas ce propos.
Solutions constructives bilatérales pour la liaison de clefs d'un instrument de musique

La pédale est liée à son maneton par des roulements suivant une liaison pivot
Pivot
d'axe (A,Z)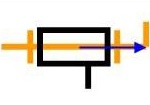
Liaisons :
Tx = 0
Ty = 0
Tz = 0
Rx = 0
Ry = 0Libertés :
RzIl est toutefois possible d'obtenir une liaison pivot par un contact simple, par deux cônes complémentaires, ou deux surfaces de révolution disposant d'une diminution de section. Pour autant cette liaison est considérée comme composée, car les surfaces considérées ici ne sont de forme triviale.
Lorsque deux solides sont en liaison pivot, il existe au moins 2 points fixes de chaque solide respectivement coïncidant. La droite passant par ces points constitue l’axe de la liaison.
Liaison glissière
La liaison glissière assure 5 degrés de liaison en ne permettant que le mouvement de translation dans la direction de la liaison. La définition de cette liaison doit préciser cette direction.
Plusieurs approches sont possibles pour réaliser cette liaison :
- à partir d’un appui plan (3 degrés de liaison) : on adjoint un second plan de contact sécant avec le premier ou, plus simplement, un axe de guidage latéral (liaison linéaire rectiligne) parallèle au plan,
- à partir d’une liaison pivot glissant (4 degrés de liaison) : une liaison ponctuelle condamnant la rotation suffit ; on parle d'anti-rotation (généralement 2 points opposés).
On pourra considérer, à un niveau plus technologique, la bilatéralité de cette liaison. Pour exemple, les tiroirs d’une commode sont guidés de façon bilatérale, alors que la voie de chemin de fer offre une liaison unilatérale dans le sens vertical.
C'est la liaison assurée dans une transmission par arbre cannelé, celle modélisant le guidage d'une coulisse de trombone ou le piston d'une trompette.
Contrairement au mouvement de rotation de la liaison pivot, l'amplitude de la translation possible est limitée par les dimensions des pièces. Lorsque le tiroir est complètement sorti, la liaison n'existe plus ! La modélisation mathématique ne prend pas en compte les limites du guidage.
La coulisse d'un trombone est liée au corps de l'instrument par une glissière, associant deux pivot glissants d'axe parallèles (solution hyperstatique).
Glissière
de direction X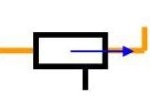

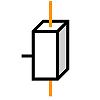
Liaisons :
Ty = 0
Tz = 0
Rx = 0
Ry = 0
Rz = 0Libertés :
TxLorsque deux solides sont en liaison glissière, il existe au moins deux droites strictement parallèles communes au deux solides, dont la direction définit la seule caractéristique géométrique de la liaison.
Par erreur, on attribue un axe à cette liaison. S'il est vrai que les solutions pour la réaliser comportent souvent des plans ou axes de symétrie, sa définition géométrique n'en a pas besoin. Des considérations de coincement par arc-boutement montrent que la disposition de la charge par rapport aux surfaces de contact peut favoriser le phénomène.
Liaison hélicoïdale
Le coulissement d'un arbre cannelé se modélise par une liaison glissière. Si on enroule les cannelures autour de l'arbre, on se trouve en présence d’une vis dans son écrou. On parle alors de liaison hélicoïdale.
Ce qui caractérise cette liaison, c’est l’existence d'un mouvement combiné : la rotation est simultanée à la translation dans un rapport qu’on appelle le pas de vis, d’hélice ou de filet. De ce fait, il s’agit d’un seul et même degré de liberté.
La liaison dispose donc de 5 degrés de liaison, dont les 2 translations et les 2 rotations transversales. L'autre est du au couplage de la translation et la rotation axiales par une relation hélicoïdale de type x = u·θx. Le pas de la liaison p = 2π·u indique la longueur parcourue en un tour (2π radians).
La définition de cette liaison doit préciser la position de son axe, le sens de l'hélice et la valeur du pas.
La considération de cette liaison est primordiale dans l'étude des dispositifs vis-écrou dont le but est de transformer un mouvement de rotation en mouvement de translation. En revanche l'étude d'un assemblage par boulons ou vis ne nécessite pas cette modélisation. Il existe des vis à billes (associées à leur écrou) destinées à la transmission de mouvement, et offrant d'excellents rendements.
Le sens de l’hélice, souvent à droite, peut être inversé. L’ancienne schématisation (toujours valable) proposée ici permet (contrairement à la nouvelle) de distinguer les deux cas.
Hélicoïdale
d'axe (A,X)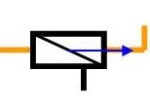
Liaisons :
x = u·θx
Ty = 0
Tz = 0
Ry = 0
Rz = 0Libertés :

Liaison rotule à doigt
La liaison sphérique à doigt dispose de 4 degrés de liaisons. Elle lie les 3 translations et une rotation, laissant libres les 2 autres rotations.
Comme son nom l'indique, il s'agit d'une rotule dotée d'un doigt faisant obstacle à une rotation. Elle apparaît sous cette forme, uniquement en tant que guidage, comme pour les des leviers de commande de boîte de vitesses ou de manette de jeu vidéo, où la rotation autour de l'axe du manche est bloquée.
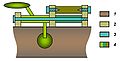
On la trouve plus couramment — avec pièce interposée — dans le joint de cardan. Elle constitue alors un organe technologique de transmission mécanique.
La définition de cette liaison doit préciser son centre, comme pour la rotule, et la direction de la rotation interdite, qui peut évoluer pendant le fonctionnement du mécanisme.

Dans un joint de Cardan, le croisillon (en vert) met les deux arbres (en rouge) en situation équivalente à une liaison directe par rotule à doigt.
Rotule à doigt
rotation Z bloquée
pas de représentation Liaisons :
Tx = 0
Ty = 0
Tz = 0
Rz = 0Libertés :
Rx, RyLa liaison complète ou encastrement
C'est le cas de deux pièces complètement solidaires. Cette liaison est parfois appelée encastrement ou liaison fixe. Elle ne présente en théorie aucune direction particulière. Sur le plan cinématique elle est sans intérêt puisque les pièces sont sans mouvement relatif possible. Cependant sur le plan technologique elle pose de vrais problèmes.
Son identification est toutefois fondamentale dans la modélisation cinématique des mécanismes puisqu'elle permet la définition des classes d'équivalence[8].
Cette liaison n'a pas de représentation définie. Le raccordement de deux lignes d'un schéma suffit à l'identifier. Lorsque le doute est possible, on peut la représenter par un secteur angulaire plein (symbole identique à une soudure d'angle en dessin technique).
Par contre sur certains schémas technologiques (non normalisés), il existe des représentations dont le souci premier est de montrer l'existence de pièces distinctes (première approche de conception). Dans ce cas son dimensionnement peut être motivé par un comportement différent suivant les directions concernées.
Sa réalisation peut reposer sur le complément d'une liaison pivot (liaison entre arbre et moyeu), ou d'un appui plan (cas des couvercles).
La liaison nulle
L'absence de contact ne contraint aucun mouvement entre deux pièces. Si sur le plan cinématique sa considération est sans intérêt, dans l'étude d'un mécanisme elle est implicitement prise en compte montrant qu'entre deux pièces données rien de plus ne vient perturber le comportement imposé par l'ensemble des autres liaisons. Un logiciel de calcul, pourra considérer une liaison nulle pièce i / pièce j n'apportant ni inconnue ni équation, mais assurant que la combinaison i / j n'a pas été oubliée.
Elle est le complément parfait de la liaison encastrement.
Modélisation mathématique des liaisons mécaniques élémentaires
A chacun des cas décrits ci-dessus correspondent des outils mathématiques exploitables pour la résolution des problèmes de mécanique. On distingue principalement deux types d'étude:
- L'étude des mouvements: en cinématique la définition d'une liaison nous renseigne sur les mouvements admissibles entre deux pièces. Elle fournit alors autant d'équations de mouvement que de degrés de liberté dans la liaison.
- L'étude des efforts: en statique, la définition d'une liaison nous renseigne sur la direction des efforts transmissibles dans la liaison. Chaque degré de liaison est alors associé à une inconnue d'effort (force ou moment).
Dans les deux cas, la formalisation mathématique possible est le torseur. Cet outil est celui utilisé dans les logiciels de mécanique du solide.
Les liaisons restent supposées parfaites, sans jeu, ni frottement, permanentes (c'est-à-dire bilatérales et sans restriction géométrique).
Cinématique
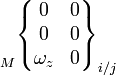
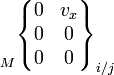
Le mouvement relatif admissible entre deux pièces i et j liées est représenté par le torseur cinématique, dont les éléments de réduction sont exprimables en un point A et une base locale (x,y,z), choisis en fonction des références centrées de la liaison considérée :
Pour une liaison définie, chaque degré de liberté supprimé annule une composante de la matrice des composantes des éléments de réductions du torseur. Les termes non nuls sont indépendants et représentent les mouvements cinématiquement admissibles dans la liaison.
L'étude globale du mécanisme nécessite ensuite, éventuellement un changement de repère pour le déroulement des calculs. La forme du torseur subit alors une modification et ne laisse plus reconnaître la liaison. Sous son nouvel aspect, il n'y a plus indépendance des composantes.
Et c'est bien dans la base locale et en un point convenablement choisis que la forme détaillée ci-dessous est valable.
Statique et dynamique
Les actions mécaniques transmissibles dans une liaison entre deux pièces i et j sont modélisables par le torseur statique de la liaison, dont les éléments de réduction (force résultante et moment ) sont exprimables en un point A et une base locale (x,y,z) choisis en fonction des références centrées de la liaison considérée.
On utilise également fréquemment la notation suivante pour écrire l'action transmissible de i sur j:
Lorsque la liaison supprime un degré de liberté, elle autorise la transmission d'un effort dans cette direction. À l'inverse, si un mouvement relatif est possible, il ne peut pas y avoir transmission d'effort. La composante correspondant de l'élément de réduction du torseur est nulle. Les termes non nuls sont indépendants et représentent les efforts transmissibles par la liaison.
Comme pour le torseur cinématique, l'étude globale du mécanisme nécessite éventuellement un changement de repère. La forme du torseur peut alors être modifiée.
Application détaillée
Le tableau ci-dessous présente les composantes des éléments de réduction des torseurs en un point particulier M dépendant du cas étudié (à choisir suivant les particularités des normales de contact).
On fera attention au cas du torseur cinématique, où le vecteur taux de rotation est situé à gauche; en effet il constitue la résultante du torseur cinématique (la rotation étant la même pour tous les points d'une pièce), et la vitesse le moment (différent en chaque point).
La connaissance de la liaison considérée élimine certaines inconnues qui prennent une valeur nulle. Pour les autres, c'est l'application de théorèmes issus des lois de la mécanique et apportant des équations qui imposera la valeur définitive.
Autres schémas cinématiques
Tout contact entre deux pièces peut aboutir à la modélisation par l'une des liaisons données ci-dessus. Ces modèles ont leur sens pour l'étude des guidages de pièces rigides, en particulier lors d'une approche statique.
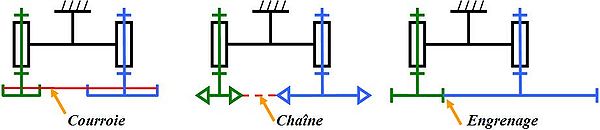
Ils sont en revanche inadaptés pour décrire les transmissions complexes lorsque l'étude à pour objectif la détermination de du mouvement globalement transmis. Par exemple, un engrenage ou une transmission par courroie s'analyse par des considérations cinématiques plus macroscopiques que les simples conditions de contact entre deux pièces (maillons de chaîne ou élément infinitésimal d'une courroie). C'est pourquoi, en ingénierie des mécanismes, d'autres joints cinématiques viennent compléter les liaisons dites rigides.
Entre pignons, par exemple, le contact s'effectue entre surfaces complexes, les points de contact évoluant au cours du mouvement. Les considérations de contact ne sont pas nécessaires à la compréhension du mouvement final; elles permettent en revanche d'analyser la réalité de la liaison : contact linéique ce qui donne le modèle à adopter dans le calcul des pressions superficielles, les conditions de glissement, le rendement énergétique…
Roues et engrenages
- Liaison roue adhérente
- Elle représente le roulement d'un disque sur une surface (non confondus) avec des frottements modélisés comme infinis ; la tangente au disque définit la direction de roulement ; cette liaison lie les 2 translations transverses et couple la rotation de la roue (autour de son axe de rotation) et le déplacement selon la direction de roulement (x = R.θ).
- Liaison pignon crémaillère
- Elle réalise le même couplage rotation translation que la liaison roue adhérente mais les déplacements transverses ne sont pas pris en charge (frottements nuls et liaison non portante).
- Liaison pignon à pignon
- Elle réalise un couplage entre les rotations des deux pignons (θ2 = a.θ1), le sens de rotation s'inversant selon que le contact est direct ou qu'il y a entraînement par chaîne ou courroie.
- Liaison pignon et vis sans fin
- Cette liaison, souvent irréversible, réalise également un couplage entre les rotations de la vis et du pignon (θ2 = u.Rv / Rp.θ1), mais par l'intermédiaire du déplacement axial de la liaison hélicoïdale.
Pour l'ensemble des cas énumérés, seul la considération cinématique globale est simplifiée. une étude statique fera appel aux degrés de liaisons, donc éventuellement à l'analyse des surfaces de transmission d'effort.
Dispositifs à corps intermédiaire
Certains nécessitent un troisième corps et peuvent donc être modélisés par un assemblage de deux liaisons :
- Joint de cardan
- Fonctionnellement très proche de la liaison sphérique à doigt présentée plus haut, il correspond à l'assemblage de deux liaisons pivots (à 90°) et s'obtient en intercalant un croisillon entre les arbres d'entrée sortie.
- Joint d'Oldham
- Très utilisé pour permettre l'accouplement de deux axes parallèles mais non parfaitement coaxiaux, il assure 4 degrés de liaison : les 3 rotations et la translation axiale, laissant libres les deux translations transverses. Il peut se modéliser comme un assemblage de deux glissières (à 90°).
- Liaison poulie
- Elle relie le déplacement du câble et de la moufle : xm = xc / nbrins.
Notes
- ↑ Une considération plus détaillée ne se justifie que dans le cas d'étude très pointue à caractère plus technologique. Elle permettrait pour l'exemple du roulement d'appréhender les contraintes aux contacts des billes avec les bagues, ou des bagues avec leurs pièces d'accueil.
- ↑ On considère des plans, des cylindres, des sphères, et parfois des cônes.
- ↑ Norme NF EN 23952 / ISO 3952-1.
- ↑ La considération des défauts de forme ou de rugosité introduirait trop tôt des concepts technologiques.
- ↑ Cette modélisation n'est pertinente que pour l'étude approfondie du comportement d'un engrenage. La considération de l'engrenage est à prendre à un niveau bien plus macroscopique (voir section Autres joints cinématiques).
- ↑ La liaison équivalente entre les bagues extérieure et intérieure de la plupart des roulements est une rotule. Suivant les modèles, le rotulage peut aller de quelques minutes d'angle à quelques degrés. Dans ce domaine de jeu aucun moment n'est transmissible. Un roulement travaillant en butée sera très vite détérioré.
- ↑ Pour les portes les plus courantes, le gond ne retient la porte que vers le bas. Il suffit alors de soulever la porte pour dégonder.
- ↑ Ensemble de pièces solidaires pendant le fonctionnement considéré du mécanisme.
Voir aussi
Bibliographie
- Norme EN 23952 / EN ISO 3952-1 : Schémas cinématiques — Symboles graphiques — Partie 1 [1]
- Michel Aublin, René Boncompain, Michel Boulaton et coll., Systèmes Mécaniques (théorie et dimensionnement), éd. Dunod (1993) ISBN 2-10-001051-4
- Jean-Louis Fanchon, Guide de mécanique — Sciences et technologies industrielles, éd. Nathan (2007), p. 114–116, 192–197, ISBN 978-2-09-178965-1
- André Chevalier, Guide du dessinateur industriel, éd. Hachette (2007), p. 115–120, ISBN 978-2-01-168831-6
- Claude Hazard, André Ricordeau, Claude Corbet, Méthode active de dessin technique, éd. Casteilla (2005), p. 155–161, ISBN 2-7135-2399-0
Liens externes
Catégorie : Théorie des mécanismes
Wikimedia Foundation. 2010.







































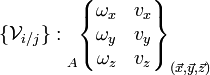
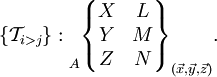

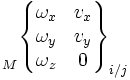
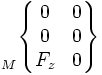
 Z
Z