Torseur statique

Pour les articles homonymes, voir Statique.

Le torseur statique, ou torseur d'action, est largement utilisé pour modéliser les actions mécaniques lorsqu'on doit résoudre un problème de mécanique tridimensionnelle en utilisant le principe fondamental de la statique. Le torseur statique est également utilisé en résistance des matériaux. On utilisait autrefois le terme de dyname^[1].

Sommaire

1 Approche « empirique »
2 Définition
3 Composantes dans un repère donné
- 3.1 Résultante du torseur
- 3.2 Moment du torseur
4 Cas particuliers
5 Torseur d'action des liaisons parfaites
6 Notes et références
7 Articles connexes

Approche « empirique »

Le torseur est un objet mathématique abstrait, dont l'étude théorique peut être rebutante pour des personnes ne l'utilisant que comme un outil. Il peut cependant être utile de le voir comme une manière d'organiser les informations.

En effet, la résolution des problèmes de statique, de dynamique et de résistance des matériaux fait intervenir les forces et les moments :

Principe fondamental de la statique (PFS): $\sum \vec{F}_{ext} = \vec{0}$; et; $\sum \vec{M}_{\vec{F}_{ext}/B} = \vec{0}$; où B est un point quelconque ;

Principe fondamental de la dynamique (PFD): $m \cdot \vec{a} = \sum \vec{F}_{ext}$; et; $J \cdot \vec{\alpha} = \sum \vec{M}_{\vec{F}_{ext}/G}$; où G est le centre d'inertie de l'objet.

Considérons deux pièces notées 1 et 2 en contact au point A. Notons $\vec{A}_{2/1}$ la force de contact de la pièce 2 sur la pièce 1 en ce point A.

Pour les problèmes hors d'un plan, les vecteurs-force ont trois composantes, et il faut utiliser des vecteurs-moment à trois composantes :

$\vec{A}_{2/1} = \begin{pmatrix} A_x \\ A_y \\ A_z \end{pmatrix}\text{ ;}$

$\vec{M}_{B}(\vec{A}_{2/1}) = \begin{pmatrix} M_x \\ M_y \\ M_z \end{pmatrix}\text{.}$

Le moment en B de la force $\vec{A}_{2/1}$ , noté $\vec{M}_{\vec{A}_{2/1}/B}$ ou $\vec{M}_{B}(\vec{A}_{2/1})$ , s'écrit :

$\vec{M}_{B}(\vec{A}_{2/1}) = \overrightarrow{BA} \wedge \vec{A}_{2/1}$

où $\wedge$ désigne le produit vectoriel.

Notons que l'action de contact entre 1 et 2 peut aussi comporter un moment $\vec{M}_{A2/1}$ en A (cas par exemple d'un tournevis qui exerce à la fois une force de pression et un couple de torsion à la vis). On a alors

$\vec{M}_{B}(\vec{A}_{2/1}) = \vec{M}_{A2/1} + \overrightarrow{BA} \wedge \vec{A}_{2/1}$ .

En notant R la résultante, on peut retenir le moyen mnémotechnique BABAR : $\vec{M}_{B} = \vec{M}_{A} + \overrightarrow{BA} \wedge \vec{R}$

On peut regrouper les composantes des deux vecteurs dans un même objet que l'on appelle « torseur », et noté :

$\{ \mathcal{T}_{2/1} \} = \begin{matrix} \\ \\ \\ \end{matrix}_B \begin{Bmatrix} A_x & M_x \\ A_y & M_y \\ A_z & M_z \\ \end{Bmatrix}_R$

où R désigne le repère dans lequel sont écrits les composantes des vecteurs. Les composantes du torseur sont en général notés X, Y, Z, L, M, N :

$\{ \mathcal{T}_{2/1} \} = \begin{matrix} \\ \\ \\ \end{matrix}_B \begin{Bmatrix} X & L \\ Y & M \\ Z & N \\ \end{Bmatrix}_R$

La résultante des actions extérieures sur la pièce 1 s'écrit

$\sum_{\mathrm{pi\grave{e}ces}\ i} \{ \mathcal{T}_{i/1} \}$

Le PFS s'écrit alors :

$\sum_{\mathrm{pi\grave{e}ces}\ i} \{ \mathcal{T}_{i/1} \} = \{ 0 \}$

et le PFD s'écrit

$\sum_{\mathrm{pi\grave{e}ces}\ i} \{ \mathcal{T}_{i/1} \} = \{ \mathcal{D} \}$

où $\{ \mathcal{D} \}$ est le torseur dynamique.

On utilise les termes de :

torseur d'action pour désigner le torseur statique décrivant l'action mécanique d'une pièce sur une autre, voir Liaison mécanique#Statique et dynamique ;
torseur de cohésion ou torseur des efforts intérieurs pour désigner le torseur statique décrivant un effort interne à une pièce (résistance des matériaux), voir Principe de la coupure.

Définition

Considérons une pièce 1 et une pièce 2 ayant un contact. Le torseur d'action de 2 sur 1 est noté

$\{ \mathcal{T}_{2/1} \} = \begin{Bmatrix} \vec{\mathcal{R}}_{2/1} \\ \vec{\mathcal{M}}_{A\ 2/1} \end{Bmatrix}$ ou bien $\{ \mathcal{T}(2 \to 1) \} = \begin{Bmatrix} \vec{\mathcal{R}}(2 \to 1) \\ \vec{\mathcal{M}}_{A}(2 \to 1) \end{Bmatrix}$

où la résultante $\vec{\mathcal{R}}_{2/1}$ représente la force exercée par le solide 2 sur le solide 1 et où le moment $\vec{\mathcal{M}}_{A\ 2/1}$ représente le couple exercé par le solide 2 sur le solide 1 au point A.

Ce torseur peut s'écrire en n'importe quel point. Le point A où l'on choisit de définir le moment est appelé « centre de réduction ».

Composantes dans un repère donné

Résultante du torseur

La résultante du torseur $\vec{\mathcal{R}}_{2 \to 1}$ est un vecteur qui peut être projeté suivant les trois axes du repère R associé. On peut donc écrire :

$\vec{\mathcal{R}}_{2 \to 1} = \begin{Bmatrix} X \\ Y \\ Z \\ \end{Bmatrix}_R$

La résultante du torseur est invariable quel que soit le point d'écriture du torseur.

L'unité internationale utilisée pour quantifier une force est le newton (N).

Moment du torseur

Le moment du torseur $\vec{\mathcal{M}}_{A\ 2 \to 1}$ est un vecteur qui possède trois composantes notées L, M, N. Le moment du torseur s'écrit alors

$\vec{\mathcal{M}}_{A\ 2 \to 1} = L \vec x + M \vec y + N \vec z$

où $\vec x$ , $\vec y$ et $\vec z$ sont les vecteurs formant la base orthonormée du repère R.

Le moment du torseur peut également être noté

$\vec{\mathcal{M}}_{A\ 2 \to 1} = \begin{Bmatrix} L \\ M \\ N \\ \end{Bmatrix}_R$

Lorsqu'on veut connaître les composantes d'un moment en un point B connaissant entièrement celles-ci en un point A et connaissant le vecteur déplacement $\overrightarrow{BA}$ , on utilise la relation de Varignon :

$\vec{\mathcal{M}}_{B\ 2 \to 1} = \overrightarrow{BA} \wedge \overrightarrow{ \mathcal{R}}_{2 \to 1} + \vec{\mathcal{M}}_{A\ 2 \to 1}$ .

L'unité internationale utilisée pour quantifier un couple est le newton mètre (N⋅m).

Cas particuliers

Un torseur dont la résultante est nulle est dit torseur couple.

Le torseur dont le moment et la résultante sont nuls est appelé le torseur nul {0}.

Lorsque le moment est perpendiculaire à la résultante, on dit que ce torseur est un glisseur :

$\vec{\mathcal{R}} \perp \vec{\mathcal{M}_{\mathrm{A}}}\text{, } \vec{\mathcal{R}} \cdot \vec{\mathcal{M}_{\mathrm{A}}} = 0$ ;

il existe un point tel que la réduction de ce torseur en ce point a un moment nul. Les torseurs représentant des forces seules sont des glisseurs, le point de réduction où le moment s'annule est le point d'application de la force.

Torseur d'action des liaisons parfaites

Au point de contact, une pièce ne peut transmettre un effort à une autre que si le mouvement relatif est bloqué. Chaque liaison mécanique bloque certaines translations et certaines rotations relatives. On peut donc connaître la forme qu'aura le torseur d'action réduit au point de contact si l'on connaît la liaison entre les pièces : le type de liaison « force » certaines composantes du torseur d'action à 0. On parle de torseur des actions mécaniques transmissibles (TAMT).

Ceci est résumé dans le tableau ci-dessous. Notez que l'emplacement des zéros dépend de l'orientation de la liaison par rapport aux axes du repère.

Liaisons	Efforts possibles
Ponctuelle	$\begin{matrix} \\ \\ _A \\ \end{matrix} \begin{Bmatrix} X & 0 \\ 0 & 0 \\ 0 & 0 \\ \end{Bmatrix}$
Linéaire rectiligne	$\begin{matrix} \\ \\ _A \\ \end{matrix} \begin{Bmatrix} X & 0 \\ 0 & 0 \\ 0 & N \\ \end{Bmatrix}$
Linéaire annulaire	$\begin{matrix} \\ \\ _A \\ \end{matrix} \begin{Bmatrix} 0 & 0 \\ Y & 0 \\ Z & 0 \\ \end{Bmatrix}$
Rotule	$\begin{matrix} \\ \\ _A \\ \end{matrix} \begin{Bmatrix} X & 0 \\ Y & 0 \\ Z & 0 \\ \end{Bmatrix}$
Pivot glissant	$\begin{matrix} \\ \\ _A \\ \end{matrix} \begin{Bmatrix} 0 & 0 \\ Y & M \\ Z & N \\ \end{Bmatrix}$
Appui plan	$\begin{matrix} \\ \\ _A \\ \end{matrix} \begin{Bmatrix} X & 0 \\ 0 & M \\ 0 & N \\ \end{Bmatrix}$
Pivot	$\begin{matrix} \\ \\ _A \\ \end{matrix} \begin{Bmatrix} X & 0 \\ Y & M \\ Z & N \\ \end{Bmatrix}$
Glissière	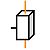$\begin{matrix} \\ \\ _A \\ \end{matrix} \begin{Bmatrix} 0 & L \\ Y & M \\ Z & N \\ \end{Bmatrix}$
Hélicoïdale	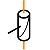$\begin{matrix} \\ \\ _A \\ \end{matrix} \begin{Bmatrix} k \cdot L & L \\ Y & M \\ Z & N \\ \end{Bmatrix}$
Rotule à doigt	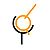$\begin{matrix} \\ \\ _A \\ \end{matrix} \begin{Bmatrix} X & 0 \\ Y & 0 \\ Z & N \\ \end{Bmatrix}$
Encastrement	$\begin{matrix} \\ \\ _A \\ \end{matrix} \begin{Bmatrix} X & L \\ Y & M \\ Z & N \\ \end{Bmatrix}$