Pierre Fermat

Pierre de Fermat

Naissance	Première décennie du XVIIesiècle Beaumont-de-Lomagne (France)
Décès	12 janvier 1665 Castres (France)
Nationalité	Française
Champs	Mathématiques et droit
Institution	Académie des Sciences Inscriptions et Belles-Lettres de Toulouse, Parlement de Toulouse
Célèbre pour	Dernier théorème de Fermat, géométrie analytique, petit théorème de Fermat, probabilité
modifier

Pierre de Fermat, né dans la première décennie du XVII^e siècle^[1],[2], à Beaumont-de-Lomagne, près de Montauban, et mort le 12 janvier 1665 à Castres, est un juriste et mathématicien français, surnommé « le prince des amateurs ».

Biographie

Son père, Dominique Fermat, était un marchand aisé, bourgeois et second consul de la ville comme marchand de cuir et autres denrées. On ne sait pas où Pierre de Fermat a effectué ses études primaires. Par la suite, il fait des études à Toulouse et de droit à Orléans. Dès 1630, il achète une charge de conseiller du roi à la Chambre des Requêtes du Parlement de Toulouse. Il épouse cette année-là Louise de Long avec qui il aura cinq enfants. Avec fidélité et assurance dans cet emploi de magistrat, il remplit sa tâche et grimpe rapidement les échelons vers des fonctions à la Chambre Criminelle et la Grand’ Chambre ; il obtiendra également d'être membre de la chambre de l'édit de Castres (1642).

Il fut membre de l'Académie des Sciences Inscriptions et Belles-Lettres de Toulouse.

Ses talents de mathématicien se sont exercés à part de son travail de magistrat puisque les grands écrits que l'on a retrouvés de lui sont des annotations dans des textes renommés tels l'Arithmetica de Diophante et une partie de sa correspondance avec les scientifiques du XVII^e siècle. Sa formation en tant que mathématicien n'est que peu connue : il semble qu'il a étudié les œuvres de François Viète qu'il trouve dans la bibliothèque d'un ami, Étienne d'Espagnet.

À ses amis mathématiciens (Beaugrand, Pascal, Descartes, Roberval, Torricelli, Huygens, Marin Mersenne), il demande de démontrer par la preuve les théories qu'il avance ce qui ravive quelquefois l'ire des autres envers lui. Il se dispute en particulier avec Descartes en 1640. En 1652, la peste qui ravage la France s'attaquera à lui, mais il y fera face et la combattra. Ce n'est qu'en 1670 que son théorème est exposé au public. Il commente, en l'étendant, Diophante, et rétablit avec une admirable sagacité plusieurs ouvrages perdus d'Apollonius (De Locis planis, Des lieux plans, en 1636) et d'Euclide. Il est en même temps un habile helléniste et un profond jurisconsulte. Ce savant cachait ses méthodes, dont quelques-unes ont été perdues avec lui.

Il s'est aussi intéressé aux sciences physiques ; on lui doit notamment le Principe de Fermat en optique.

Après sa mort

Pierre de Fermat

Il ne reste après son décès qu'une importante correspondance dispersée dans toute l'Europe.

Le fils de Pierre de Fermat publie, en 1670, une édition de l'Arithmetica de Diophante, annoté par son père, puis en 1679 une série d'articles et une sélection de sa correspondance sous le nom de Varia opera mathematica.

En 1839, Guglielmo Libri tente de soustraire un certain nombre de manuscrits, dont une partie seulement sera récupérée.

Charles Henry et Paul Tannery publient, au début du XX^e siècle, les Œuvres de Fermat en quatre volumes ; un supplément sera ajouté par C. de Waard en (1922).

Contributions

Il partage avec Viète, dont il use des notations^[3],[4], et Descartes, avec qui il fut en conflit^{[5],[6] [7] [8] [9]} , la gloire d'avoir appliqué l'algèbre à la géométrie. Il imagina pour la solution des problèmes, une méthode, dite de maximis et minimis, qui le fait regarder comme le premier inventeur du calcul différentiel dont il est un précurseur : il est le premier à utiliser la formule (sinon le concept) du nombre dérivé (en réalité ce concept a été découvert par un grand mathématicien indien, Aryabhata).

Il pose en même temps que Blaise Pascal les bases du calcul des probabilités. Mais sa contribution majeure concerne la théorie des nombres et les équations diophantiennes. Auteur de plusieurs théorèmes ou conjectures dans ce domaine, il est au cœur de la « théorie moderne des nombres ».

Il est très connu pour deux « théorèmes » :

• le « petit théorème de Fermat » ;
• le « dernier théorème de Fermat » ; ce dernier n'était qu'une conjecture et l'est resté durant plus de trois siècles de recherches fiévreuses.

Petit théorème de Fermat

Si p est un nombre premier et a un entier naturel non divisible par p, alors .

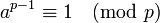Voir aussi : Théorème d'Euler, dont ce théorème est un cas particulier.

Théorème des deux carrés de Fermat

Ce théorème énonce que pour qu'un nombre premier impair soit la somme de deux carrés, il faut et il suffit qu'il soit congru à 1 modulo 4.

Théorème de Fermat sur les nombres polygonaux

Buste dans la salle des Illustres du Capitole de Toulouse

Tout entier s'écrit :

• comme somme d'au plus 3 nombres triangulaires
• comme somme d'au plus 4 nombres carrés
• comme somme d'au plus 5 nombres pentagonaux
• etc.
  • nombres triangulaires :
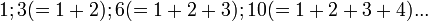     : le n-ième nombre triangulaire est égal à la somme des n premiers entiers naturels non nuls ;
  • nombres carrés :
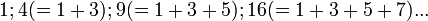     : le n-ième nombre carré est égal à la somme des n premiers entiers naturels impairs)
  • nombres pentagonaux :
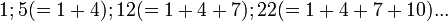     : le n-ième nombre pentagonal est égal à la somme des n premiers entiers naturels congrus à 1 modulo 3 ;
  • nombres polygonaux d'ordre m  :
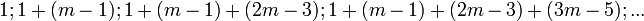     : le n-ième nombre polygonal d'ordre m est égal à la somme des n premiers entiers naturels congrus à 1 modulo (m-2).

Ce théorème a été énoncé par Fermat, démontré dans le cas des nombres carrés par Jacobi et, indépendamment par Joseph-Louis Lagrange au XVIII^e siècle (Ce dernier se servant de résultats partiels obtenus par Euler). Gauss résolut le cas des nombres triangulaires en 1796. Une preuve complète a été proposée par Cauchy en 1813.

Grand théorème de Fermat (ou dernier théorème de Fermat)

Travail de Diophante d'Alexandrie traduit du grec en latin par Claude-Gaspard Bachet de Méziriac. Cette édition du livre a été publiée en 1621. La page 85 contient le problème II.VIII de Diophante, et est la page sur laquelle Pierre de Fermat écrivit que la marge était trop petite pour contenir la démonstration.

« Il n'existe pas d'ensemble d'entiers strictement positifs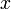 , , 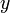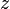vérifiant l'équation 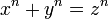lorsque n est un entier tel que . »

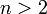Ce théorème fut démontré par le mathématicien anglais Andrew Wiles de l'Université de Princeton, avec l'aide de Richard Taylor. Après une première présentation en juin 1993, puis la découverte d'une erreur et un an de travaux supplémentaires, la preuve fut finalement publiée en 1995 dans Annals of Mathematics.

Pierre de Fermat lui-même annotait dans la marge de son exemplaire des Arithmétiques qu’il en avait découvert une démonstration vraiment remarquable, mais manquait de place pour la donner à cet endroit:"j'ai découvert une preuve réellement remarquable que cette marge trop étroite ne me permet pas de détailler".

La démonstration évoquée par Pierre de Fermat est soit fausse, soit inconnue à ce jour, car la démonstration réalisée par Andrew Wiles utilise des outils mathématiques dont M. de Fermat ne pouvait vraisemblablement disposer compte tenu des connaissances de son époque.

Méthode de la descente infinie

Fermat est l'inventeur d'une méthode de démonstration, la descente infinie : Supposons qu'une proposition P dépendant d'un rang n (> 0) vérifie la propriété : « Si P est vraie à un rang quelconque r, elle l'est à un certain autre rang q strictement inférieur à r ». Alors on peut conclure que P est fausse pour tout rang. En effet, pour tout r, l'application récurrente de la propriété permet de construire une chaîne infinie de rangs décroissants r > q >...>... Or les rangs étant positifs, la longueur de la chaîne ne peut pas être supérieure à r.

La descente infinie peut être utilisée pour démontrer le cas particulier n = 4 du dernier théorème de Fermat.

Principe de Fermat (optique)

Le trajet parcouru par la lumière entre deux points est toujours celui qui optimise le temps de parcours. Voir l'article principe de Fermat.

Dans la culture populaire

Cinéma

• Dans le film espagnol du nom de "La habitación de Fermat" ("La chambre de Fermat"), cinq mathématiciens se retrouvent sur l'invitation anonyme d'un certain "Fermat", et se voient affublés de noms de mathématiciens célèbres en tant que pseudonymes pour la soirée.

Références

Bibliographie

• Émile Brassinne, Précis des œuvres mathématiques, Toulouse, 1853.
• Paul Tannery, Charles Henry et C. de Waard, Œuvres de P. Fermat, Gauthier-Villars et cie, Paris, 1891-1922, 5 vol. 23×29 cm 
• Paul Féron, Pierre de Fermat : un génie européen (avec le concours de Jacques Arlet, Henri Gilles, Georges Passerat [et al.]), Toulouse : Presses de l'Université des sciences sociales de Toulouse et Éditions toulousaines de l'Ingénieur, 2002, 224 p. (ISBN 2-909628-83-3)
• Simon Singh, Le dernier théorème de Fermat (ISBN 2-7096-1854-0)
• André Dupuy, Pierre Fermat
• Giulio Giorello et Corrado Sinigaglia (trad. A. Masé, G. Idabouk et al.), Pierre Fermat [« Pierre de Fermat, I sogni di un magistrato alle origini della matematica moderna »], Pour la science, coll. « Dossiers Pour la science / les génies de la science », 2007, n°32, magazine, 102 p. (ISBN 2-84245-091-1) (ISSN 1298-6879) [présentation en ligne] 

Articles connexes

• Prix Fermat de recherche en mathématiques
• Nombre de Fermat
• 4 294 967 297
• Principe de Fermat
• Mathématiques en Europe au XVIIe siècle

Liens externes

• Œuvres de Fermat publiées par les soins de MM. Paul Tannery et Charles Henry sous les auspices du Ministère de l'instruction publique.
• Œuvres de Fermat en ligne sur archive.org : t.1, Paris, 1891 ; t.2, 1894; t.3, 1896 ; t.4, 1912.
• Méthode de Fermat pour la recherche du minimum et du maximum, analysée sur le site BibNum.
• Exposition permanente à Beaumont de Lomagne

• Portail des mathématiques
• Portail de la physique
• Portail de la France du Grand Siècle (1598-1715)
• Portail de Tarn-et-Garonne