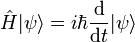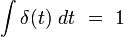PAM Dirac

Cet article fait partie de la série Mécanique quantique

Postulats de la mécanique quantique Histoire de la mécanique quantique Concepts fondamentaux État quantique · Superposition · Observable · Intrication · Mesure · Principe d'incertitude · de correspondance · Dualité · Décohérence Expériences Fentes de Young · Expérience de Stern et Gerlach · Chat de Schrödinger · Gomme quantique · Paradoxe EPR · Téléportation quantique · Expérience d'Aspect Formalisme Notation Bra-Ket · Équation de Schrödinger · Matrice densité · Représentation de Schrödinger · de Heisenberg · d'interaction Statistiques Maxwell-Boltzmann · Échange · Fermi-Dirac · Fermion · Bose-Einstein · Boson Théories avancées Théorie quantique des champs · Axiomes de Wightman · Électrodynamique quantique · Chromodynamique quantique · Gravité quantique · Diagramme de Feynman Interprétations Problème de la mesure · Copenhague · Ensemble · Variables cachées · Transactionnelle · Mondes multiples · Histoires consistantes · Logique quantique · Réduction par l'observation (consciente) Physiciens Planck · de Broglie · Schrödinger · Heisenberg · Bohr · Pauli · Born · Dirac · von Neumann · Einstein · Bohm · Feynman · Everett · Penrose

Paul Adrien Maurice Dirac est un physicien et mathématicien britannique né le 8 août 1902 à Bristol et mort le 20 octobre 1984 à Tallahassee, Floride (États-Unis).

Il est l'un des « pères » de la mécanique quantique et reste célèbre pour avoir prévu l'existence de l'antimatière (positron).

Sommaire 1 Biographie 2 Bibliographie 3 Voir aussi 3.1 Liens internes

Biographie

Son père, Charles Dirac, est originaire de Suisse, dans le canton du Valais. Il s'établit à Bristol et se marie avec Florence Holten avec qui il aura trois enfants : Charles Félix Dirac, Isabelle Marguerite Béatrice et Paul (le cadet). Sa famille paternelle est issue de la ville de Dirac en Charente.

À l'école primaire de sa ville natale, Paul montre ses qualités exceptionnelles dans le domaine des mathématiques. Dès 12 ans, il entre à l’école secondaire où son père enseignait. À cette période commence la Première Guerre mondiale qui aura un effet bénéfique pour Paul. Car depuis l'ancienne école jusqu’au service militaire, les jeunes garçons avaient plus facilement accès à la Science et aux laboratoires.

Au collège technique, très jeune, il est initié aux mathématiques, à la physique et la chimie. Il étudie les mathématiques avec des livres en avance sur les programmes des classes qu’il fréquentait et cette avance a été d'une grande aide en dernière année. Il étudie les mathématiques à l'université de sa ville natale et entre à partir de 1923 à l'université de Cambridge, où il aura pour superviseur Ralph Fowler. En 1925, il rencontre Niels Bohr, puis Werner Heisenberg. Dans les six mois suivant son arrivée à Cambridge, il publie deux documents en mécanique statistique et en physique quantique des atomes. En mai 1924, Dirac termine son premier document traitant des problèmes quantiques et quatre autres sont achevés en novembre 1925. Durant sa période de thèse, un événement douloureux va se produire dans sa vie : son frère Charles Dirac se suicide.

En 1926, il constate que le principe d'incertitude de Heisenberg était une déclaration à la non commutativité de la mécanique quantique, il démontre l'équivalence physique de la mécanique ondulatoire et de la mécanique des matrices. Il réalise l'analogie avec les crochets de Poisson dans la mécanique hamiltonienne.

Il formule aussi une théorie quantique mathématiquement cohérente en assemblant les idées de Schrödinger et Heisenberg. Dirac a publié onze articles dans la presse avant de soutenir sa thèse de doctorat. Après sa thèse, il part travailler avec Bohr à Copenhague. Il rejoint Göttingen en 1927. En septembre, il est invité au cinquième congrès Solvay où il rencontre Albert Einstein.

En 1928, il déduit du travail de Pauli sur un système de spins non-relativiste une équation relativiste décrivant l'électron, et contenant en soi le spin. Elle est appelée aujourd'hui équation de Dirac. Cela permet à Dirac de prédire en 1931 l'existence d'une particule appelée positron, l'antiparticule de l'électron. Il faudra attendre 1932 pour qu'Anderson et Patrick Blackett observent enfin cette particule.

Dans Les principes de la mécanique quantique, publié en anglais en 1930^[1], il utilise l'algèbre des opérateurs linéaires comme une généralisation des théories d'Heisenberg et de Schrödinger. Il introduit ainsi la notation bra-ket, pour laquelle 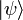est un vecteur d'état dans l'espace des états du système, et 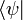un vecteur de l'espace dual correspondant.

Il partage le prix Nobel de physique en 1933 avec Erwin Schrödinger pour « la découverte de formes nouvelles et productives de la théorie atomique ». Cette même année, il publie un document sur le lagrangien en mécanique quantique qui inspirera Richard Feynman. Il se marie une année plus tard avec Margit Wigner, la soeur du physicien Eugene Wigner, avec qui il aura deux filles et adoptera d’autres enfants de Margit d’un précédent mariage dont Gabriel Andrew Dirac qui deviendra mathématicien, et contribuera à la théorie des graphes.

Dirac fut « Professeur Lucasien » à l'université de Cambridge^[2] de 1932 à 1969 et professeur de premier cycle à l'université de Bristol. Il est lauréat de la Royal Medal en 1939 et de la médaille Copley en 1952. En 1970, il rejoint l'université de Floride et s'installe à Tallahassee où il meurt 14 années plus tard.

Pour les besoins du formalisme quantique, Dirac a introduit un objet singulier, qu'on appelle aujourd'hui impulsion de Dirac ou masse de Dirac, notée δ(t). Cette impulsion représente un signal de durée théoriquement nulle et d'énergie infinie, et doit vérifier la condition :

Ce concept d'impulsion n'avait pas de fondement mathématique précis : en particulier, il ne pouvait pas s'agir d'une fonction ordinaire, car une fonction qui est nulle presque partout possède une intégrale identiquement nulle, d'après la théorie de l'intégration de Lebesgue. Le mathématicien Laurent Schwartz a inventé l'outillage adéquat pour décrire rigoureusement ce genre d'objets, la théorie des distributions.

Communément, on dit d'une mesure qu'elle est de Dirac si toute la densité est concentrée en un point unique. Pour Dirac, seule la beauté mathématique de la théorie primait, il n’avait pas été très influencé par les résultats expérimentaux. Ce qui donna son célèbre classique de mécanique quantique et un excellent ouvrage de relativité générale.

Bibliographie

• Paul Dirac, Les principes de la mécanique quantique, Presses polytechniques et universitaires romandes, 2009 (ISBN 978-2-88074-800-5). Traduction de la dernière édition (c'est-à-dire la quatrième édition de 1958 dans sa version révisée de 1967). Cet ouvrage de référence est l'aboutissement de trente-sept ans de perfectionnements depuis sa première version de 1930.
• (en) Helge S. Kragh, Dirac: a scientific biography, Cambridge university press, 1990 (ISBN 0-521-38089-8)
• (en) PAM Dirac ; General theory of relativity, John Wiley (1975). Réédité par Princeton university press (1996) ISBN 0-691-01146-X. Courte introduction à la théorie de la relativité générale basée sur un cours fait par l'auteur à l'université de Tallahassee, en Floride.

Voir aussi

Liens internes

•  Paul Dirac sur Commons
• Chaire de professeur lucasien de mathématiques de l'université de Cambridge
• Distribution de Dirac
• Équation de Dirac
• Fonction δ de Dirac
• Peigne de Dirac
• Constante de Planck réduite (dite aussi constante de Dirac)
• Particule de Dirac
• Notation de Dirac

Précédé de : Werner Heisenberg

Prix Nobel de physique 1933

Suivi de : James Chadwick

• Portail de la physique