Approximant de Padé

Le concept de l'article doit son nom à Henri Padé (1863 - 1953) un mathématicien français.

En mathématiques, et plus précisément en analyse complexe, l'approximant de Padé est une méthode d'approximation d'une fonction analytique par une fonction rationnelle. En ce sens, elle est un peu analogue à un développement limité qui approche la fonction selon les mêmes critères à l'aide d'un polynôme.

De même que les développements limités forment une suite appelée série entière, convergeant vers la fonction initiale, les approximants de Padé sont souvent vus comme une suite, s'exprimant sous la forme d'une fraction continue dont la limite est aussi la fonction initiale. En ce sens, ces approximants font partie de la vaste théorie des fractions continues.

En analyse complexe, les approximants offrent un développement dont le domaine de convergence est parfois plus large que celui d'une série entière. Ils permettent ainsi de prolonger des fonctions analytiques et d'étudier certains aspects de la question des série divergentes. En théorie analytique des nombres, l'approximant permet de mettre en évidence la nature d'un nombre ou d'une fonction arithmétique comme celle de la fonction zêta de Riemann. Dans le domaine du calcul numérique, l'approximant joue un rôle, par exemple, pour évaluer le comportement d'une solution d'un système dynamique à l'aide de la théorie des perturbations.

L'approximant de Padé est utilisé pour la première fois par Leonhard Euler (1707 - 1783), pour démontrer l'irrationalité de e, la base du logarithme népérien. Une technique analogue permet à Johann Heinrich Lambert (1707 - 1777) de montrer celle de π. Cette notion est développée plus systématiquement par Henri Padé (1863 - 1953) et érigée en théorie à part entière.

Préambule

Présentation du concept

Charles Hermite utilise ce qui est maintenant appelé un approximant de Padé pour démontrer la transcendance de $\scriptstyle e$ en 1873.

Il s'avère utile de pouvoir approcher une fonction donnée par une suite de fonctions aisément calculables. Cette démarche est à l'origine de la théorie des séries entières consistant à approcher de plus en plus précisément une fonction analytique à l'aide de la suite de ses développements limités. La théorie associée dépasse de loin le cadre du calcul numérique. Les développements limités, puis les séries entières offrent de nombreuses possibilités comme le calcul d'une limite ou la résolution d'une équation différentielle.

La démarche de Padé est, à beaucoup d'égards, analogue à celle des séries entières. L'objectif est d'approcher le mieux possible une fonction analytique à l'aide d'une fraction rationnelle. Le mieux possible signifie ici que, pour un couple ( $\scriptstyle p$ , $\scriptstyle q$ ) d'entiers positifs donné la fraction rationnelle $\scriptstyle h(t) / k(t)$ est telle que $\scriptstyle h(t)$ et $\scriptstyle k(t)$ sont des polynômes dont le degré ne dépasse respectivement pas $\scriptstyle p$ et $\scriptstyle q$ et son développement limité colle le mieux possible à celui de la fonction $\scriptstyle f(t)$ . En règle générale, les deux développements limités coïncident jusqu'à l'ordre $\scriptstyle p + q$ . Une telle fraction est un approximant de Padé de la fonction $\scriptstyle f(t)$ .

De même qu'il est intéressant de considérer la suite des développements limités, il est judicieux d'étudier les suites d'approximants, de plus en plus précises et convergeant vers la fonction $\scriptstyle f$ . Ses suites peuvent toujours s'exprimer sous forme de fractions continues. Dans le cas des polynômes, les développement limités sont indexés par un entier positif, ce qui engendre une suite naturelle : la série entière. Les approximants de Padé sont indexés par un couple d'entiers positifs, engendrant une infinité de suites possibles et complexifiant la démarche. D'autres causes rendent l'approche plus complexe. La somme, le produit, la dérivée ou la primitive d'approximant de Padé n'ont aucune raison d'être encore un approximant de Padé.

Ces suites offrent néanmoins quelques avantages que n'ont pas les séries entières. La nature arithmétique d'un nombre comme π ou la base du logarithme népérien est plus simplement mise en valeur. Les preuves de l'irrationalité de $\scriptstyle \pi$ et de $\scriptstyle e$ , comme celles de leur transcendance, se fondent naturellement sur cet outil (voir Fraction continue et approximation diophantienne). Les suites d'approximants de Padé possèdent parfois un autre avantage. Certaines fonctions sont initialement définies par des séries dont le domaine de convergence est limité par la présence des pôles, comme la fonction zêta de Riemann. Une expression sous forme de suite d'approximants de Padé ne possède pas nécessairement cette faiblesse. Le caractère parfois plus vaste du domaine de convergence d'une suite d'approximants de Padé par rapport à une expression sous forme de série entière est un atout non négligeable. La physique ou l'astronomie offrent des exemples d'application. L'étude d'un système dynamique un peu complexe peut nécessiter le recours à la théorie des perturbations, les solutions sont souvent des fonctions analytiques exprimées sous forme de séries entières. Or la présence de pôles impose parfois un rayon de convergence trop petit pour permettre un calcul effectif intéressant. Ce phénomène se traduit par le besoin de calculer la limite d'une série divergente. Trouver une bonne suite d'approximants de Padé permet d'élargir le domaine de convergence, le comportement de la fonction analytique est ainsi connu sur une plus vaste étendue et le calcul effectif de la limite est possible.

Approche par la fraction continue

Article détaillé : Fraction continue.

Une fraction continue permet d'approcher un nombre réel avec une précision aussi bonne que souhaitée. Une démarche analogue peut être appliquée aux fonctions analytiques. Une fonction analytique $\scriptstyle f$ se développe en série entière, si $\scriptstyle t_0$ est un point de domaine de définition de $\scriptstyle f$ et $\scriptstyle t$ un scalaire de module strictement inférieur à r, le rayon de convergence de $\scriptstyle f$ au point $\scriptstyle t_0$ , il est possible de développer $\scriptstyle f$ de la manière suivante : $\scriptstyle f(t_0 + t) = \alpha_0 + \alpha_{n_1} \cdot t^{n_1} + \ldots$ . Ici, $\scriptstyle \alpha_{n_1}$ ainsi que les coefficients suivants sont choisis différents de 0. Pour cette raison, $\scriptstyle n_1$ n'est pas nécessairement égal à 1. Il existe une fonction analytique $\scriptstyle f_1$ tel que 0 soit élément de son domaine de définition et :

$f(t_0 + t) = a_0 + \frac {t^{n_1}}{f_1(t)}\quad\text{avec}\quad a_0 = \alpha_0$

Un traitement analogue sur la fonction $\scriptstyle f_1$ , puis $\scriptstyle f_2$ montre qu'il est encore possible d'écrire la fonction f de la manière suivante :

$f(t_0 + t) = a_0 + \cfrac {t^{n_1}}{a_1 + \cfrac {t^{n_2}}{f_2(t)}} = a_0 + \cfrac {t^{n_1}}{a_1 + \cfrac {t^{n_2}}{a_2 + \cfrac {t^{n_3}}{f_3(t)}}} = \cdots$

Cet algorithme permet d'approcher la fonction analytique $\scriptstyle f$ par une fraction rationnelle. Si $\scriptstyle f$ est elle-même une fraction rationnelle, il existe une valeur $\scriptstyle p$ tel que $\scriptstyle f_p$ soit une fonction constante et le processus s'arrête, dans le cas contraire, le processus continue indéfiniment. Cette configuration est analogue à celle des nombres rationnels pour la fraction continue.

Pour une raison de commodité, les notations suivantes, dites de Pringsheim sont utilisées dans cet article :

$f(t_0 + t) = a_0 + \frac{t^{n_1}\mid}{\mid a_1} + \frac{t^{n_2}\mid}{\mid a_2} + \frac{t^{n_3}\mid}{\mid a_3} +\dots$

Si le processus est arrêté à la $\scriptstyle p^{\text{e}}$ étape, on obtient une fraction rationnelle qui approche la fonction initiale $\scriptstyle f$ . Cette fraction rationnelle est un exemple d'approximant de Padé. Pour une raison de simplicité, dans la suite de l'article la valeur $\scriptstyle t_0$ est choisie égale à 0.

Fonction tangente

Pour illustrer cette démarche, considérons la fonction tangente, l'un des premiers exemples historiques^[1] de fonction analytique dont des approximants de Padé sont calculés :

$\tan (t) = \cfrac t{1 - \cfrac {t^2}{3 - \frac {t^2} {5 - \frac {t^2}{7 - \cdots}}}} = \frac{t \mid}{\mid 1} - \frac{t^2 \mid}{\mid 3} - \frac{t^2 \mid}{\mid 5} - \frac{t^2 \mid}{\mid 7} + \cdots$

Un premier calcul, réalisé par Lambert montre l'égalité des deux développements mais il n'étudie pas la convergence, que rien ne garantit. Une analyse plus précise montre que si t n'est pas de la forme kπ + π/2, où k est un entier, le terme de droite tend vers tan(t).

Appliquons l'algorithme du paragraphe précédent au point t₀ = 0. La valeur a₀ est égale à 0 et n₁ à 1. On obtient une première fraction rationnelle h₀(t) / k₀ (t) approchant la fonction tangente :

$\tan(t) = 0 + \frac t{f_1(t)},\quad f_1(t) = \frac t{\tan(t)}\quad\text{et}\quad h_0(t) = 0,\; k_0(t) = 1$

Il est plus simple d'exprimer f₁ à l'aide des développements en séries entières des fonctions sinus et cosinus pour prolonger les calculs :

$f_1(t) = \cfrac {t\cos (t)}{\sin (t)} = \cfrac {1 - \frac {t^2}2 + \cdots}{1 - \frac {t^2}6 + \cdots} = {1 - \cfrac{(1-1) + (\frac 12 - \frac 16)t^2 + \cdots} {1 - \frac {t^2}6 + \cdots}} = 1 - \cfrac {\frac {t^2}3 - \frac {t^4}{30} + \cdots}{1 - \frac {t^2}6 + \cdots} = 1 - \frac {t^2}{f_2(t)}$

On obtient une nouvelle expression plus précise de la fonction tangente :

$\tan(t) = 0 + \frac{t \mid}{\mid 1} - \frac{t^2 \mid}{\mid f_2(t)},\quad f_2(t) = \cfrac {1 - \frac {t^2}6 + \cdots} {\frac 13 - \frac {t^2}{30} + \cdots}\quad\text{et}\quad h_1(t) = t,\; k_1(t) = 1$

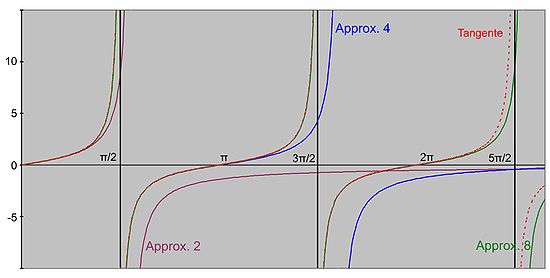
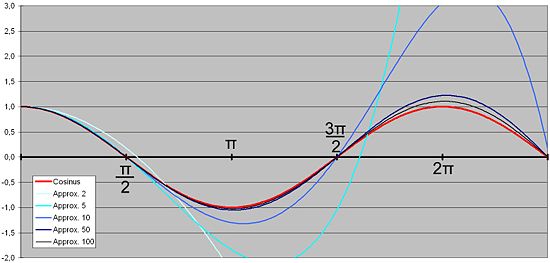
Si l'expression en fraction continue est réduite au même dénominateur, et si la fraction est noté h_n(t) / k_n (t), Il devient possible de déterminer une expression par récurrence, puis de représenter graphiquement ces différentes approximations :

$\forall n \ge 2\quad h_n(t) = (2n-1)h_{n-1}(t) -t^2h_{n-2}(t) \quad \text{et}\quad k_n(t) = (2n-1)k_{n-1} -t^2k_{n-2}(t)$

Dans cet exemple, la suite des approximants de Padé, avale les pôles et fournit une approximation sur tous les nombres réels, à l'exception des pôles.

Les approximations successives permettent d'avaler les pôles de la fonction tangente. Sur les réels positifs, la deuxième approximation, en violet sur la figure, simule le premier pôle avec une asymptote à √3 au lieu de π/2. La quatrième approximation, en bleu, ne diffère pas de manière visible de la fonction tangente, en rouge sur le graphique, sur l'intervalle [0, π]. Elle possède deux pôles sur les réels positifs. La huitième approximation, en vert, colle à la fonction tangente sur l'intervalle [0, 2π] et possède 4 pôles positifs dont 3 sont visibles sur la figure. De manière plus générale, si n est un entier strictement positif et ε un réel strictement positif, la suite des approximants converge uniformément sur la réunion des intervalles [0, π/2 - ε] et [(2j-1)π/2 - ε, (2j+1)π/2 + ε] où j varie de 1 à n.

Cette capacité à avaler les pôles est l'un des attraits des approximants de Padé, d'autant plus fort que ce résultat reste valable si les fonctions sont considérées comme complexes de la variable complexe. À la différence des séries entières les approximants de Padé fournissent des informations sur la fonction tangente en dehors du disque de rayon π/2. Cette propriété est utilisée pour l'étude de la fonction zêta de Riemann. De manière plus simple, cette fraction continue est l'outil essentiel de la première démonstration de l'irrationalité de π (cf Fraction continue et approximation diophantienne).

Démonstration moderne

Montrons dans un premier temps ce résultat si a est égal à 1 :

Une récurrence montre que la suite de fonctions (k_n(t)) est strictement croissante et tend vers plus l'infini et ceci pour toute valeur de t choisie dans l'intervalle [0,1]. La méthode utilisée ici consiste à étudier la suite de fonctions (ψ_n(t)), définie de la manière suivante :

$\forall t \in [0,1],\; \forall n \in \mathbb N\quad \quad \psi_n(t) = k_n(t)\sin t - h_n(t) \cos t$

L'objectif est de montrer que cette suite de fonctions strictement croissantes tend uniformément vers la fonction nulle. Pour cela, établir un lemme s'avère nécessaire :

La dérivée de ψ_n(t) est égale à t.ψ_n-1(t) :

Montrons ce résultat par récurrence, à l'ordre 1, le calcul suivant le montre :

$\psi_1'(t)=\frac d{dt}\Big(\sin (t) - t\cos(t)\Big) = \cos (t) -\cos (t) + t\sin (t) = t\psi_0(t) \;$

Supposons le résultat établi à l'ordre n et montrons le pour n + 1. On dispose de l'égalité suivante :

$\psi_{n+1}'= \frac d{dt}\Big(k_{n+1}\sin - h_{n+1} \cos \Big) = (k'_{n+1}+ h_{n+1})\sin + (k_{n+1} - h'_{n+1})\cos$

Calculons le premier terme de cette dérivée :

$k'_{n+1}+ h_{n+1} = \frac d{dt}\Big((2n+1)k_n - t^2k_{n-1}\Big) + (2n+1)h_n -t^2 h_{n-1}= (2n+1)(k'_n + h_n) -2tk_{n-1} - t^2 (k'_{n-1} + h_{n-1})$

L'hypothèse de récurrence établit la première égalité et permet de déduire le résultat :

$k'_n + h_n = tk_{n-1}\quad\text{donc}\quad k'_{n+1}+ h_{n+1} = t\big((2n+1)k_{n-1} -2k_{n-1} - t^2k_{n-2}\big)= t\big((2n-1)k_{n-1} -t^2k_{n-2}\big) = tk_n \;$

Le deuxième terme prend la forme suivante :

$k_{n+1}- h'_{n+1} = (2n+1)k_n - t^2k_{n-1} - \frac d{dt}\Big((2n+1)h_n -t^2 h_{n-1}\Big)= (2n+1)(k_n - h'_n) +2th_{n-1} - t^2 (k_{n-1} - h'_{n-1})$

En raisonnant comme précédemment :

$k_n - h'_n = -th_{n-1}\quad\text{donc}\quad k_{n+1}- h'_{n+1} = t\big(-(2n+1)h_{n-1} +2h_{n-1} + t^2h_{n-2}\big)= -t\big((2n-1)h_{n-1} -t^2h_{n-2}\big) = -th_n \;$

Ce qui démontre la proposition recherchée.

La suite des fonctions (ψ_n) est composée de fonctions positives strictement croissantes et la suite converge uniformément vers zéro :

On remarque que la suite (h_n) est composée de fonctions impaires, donc nulles en zéro, on en déduit que la suite (ψ_n) est composée de fonctions nulles en 0. La fonction ψ₀ a pour dérivée t.sin(t), qui est strictement positive sauf au point 0, ce qui montre que la fonction est strictement croissante. Par récurrence, la fonction ψ_n possède une dérivée strictement positive sauf en 0, car elle est égale à tψ_n-1(t) est elle donc strictement croissante. Comme elle est nulle en 0, elle est positive.

Le maximum de la fonction ψ_n est atteint au point 1, car elle est strictement croissante, pour montrer l'uniforme convergence de la suite (ψ_n) vers la fonction nulle, il suffit donc de montrer que (ψ_n(1)) est une suite qui tend vers 0. Montrons par récurrence que ψ_n(1) est majoré par sin(1)/2ⁿ. Pour n égal 0, le résultat est vrai car ψ₀(1) = sin(1) - cos(1) < sin(1). Supposons le résultat vrai à l'ordre n et montrons le à l'ordre n + 1 :

$\psi_{n+1}(1) = \int_{0}^1 t\psi_n(t)\, \mathrm dt < \int_{0}^1 t\frac {\sin (1)}{2^n} \, \mathrm dt = \frac {\sin (1)}{2^{n+1}}$

Conclusion :

On dispose de l'égalité suivante :

$\forall t \in [0,1]\quad 0 < \tan (t) - \frac {h_n(t)}{k_n(t)} = \frac {\psi_n(t)}{\cos (t) k_n(t)}< \frac {\tan (1)}{2^n k_n(1)}\;$

Si n tend vers l'infini, 2ⁿ ainsi que k_n(1) tendent vers l'infini, ce qui montre l'uniforme convergence de la suite des fractions réduites vers la fonction tangente. La convergence est étudiée sur un domaine plus vaste en fin d'article.

Démonstration historique de Lambert

La détermination précédente de l'approximant de Padé de la fonction tangente n'est pas celle de Lambert. Il procède de la manière suivante : la fonction tangente admet un développement en série entière t + .... Il écrit cette fonction tan (t) = t/R₁(t). Comme la fonction tangente est une série entière, il en est de même pour R₁(t), il en détermine une expression comme un quotient de deux séries entières paires. Son coefficient constant est égal à 1, il en déduit une expression de R₁(t) de la forme suivante : 1 - t²/R₂(t) où R₂(t) s'exprime comme le quotient de deux séries entières. À l'aide d'une relation de récurrence, il détermine l'expression de R_n(t) et en déduit un approximant de Padé.

Cette approche possède deux faiblesses. Dans un premier temps, on peut remarquer que l'expression exacte de R_n(t) est lourde, impliquant des calculs bien laborieux. Il existe une faille plus grave dans son approche : le comportement de R_n(t) n'est pas étudié. Si cette fonction ou son rayon de convergence tend vers 0, alors la suite des fractions réduites ne converge pas nécessairement vers la fonction tangente. Une fois la fraction continue explicitée, il devient nécessaire d'étudier sa convergence, ce qui revient au même qu'un des calculs de la boite déroulante précédente, l'expression directe de R_n(t) étant trop lourde pour une analyse directe.

Pour cette raison, sa démonstration n'est pas toujours considérée comme la première preuve de l'irrationalité de π. Néanmoins, les historiens l'estiment souvent comme valide^[2] en tenant compte du fait que les critères de rigueur de l'époque ne sont pas ceux d'aujourd'hui.

Si t est un élément de l'intervalle [0, 1], la suite des quotients incomplets suivante sont les approximants de Padé :

$\tan{t} = \cfrac{t}{1 - \cfrac{t^2}{3 - \cfrac{t^2}{5 - \cfrac{t^2}{\cdots}}}}$

Les développements en série entières des fonctions cosinus et sinus montrent que :

$\forall t \in [0,1] \quad \tan t = \frac {\sin t}{\cos t} = \frac { t - \frac {t^3}6 + \cdots + (-1)^n\frac {t^{2n+1}}{(2n+1)!}+ \cdots }{ 1 - \frac {t^2}2 + \cdots + (-1)^n\frac {t^{2n}}{(2n)!}+ \cdots }= t \frac {\sum_0^{\infty} (-1)^n\frac {t^{2n}}{(2n+1)!}}{\sum_0^{\infty}(-1)^n\frac {t^{2n}}{(2n)!}}$

On en déduit l'expression suivante :

$\tan t = \frac t{\frac {\sum_0^{\infty}(-1)^n\frac {t^{2n}}{(2n)!}}{\sum_0^{\infty} (-1)^n\frac {t^{2n}}{(2n+1)!}}} = \frac t{1 + \frac {\sum_0^{\infty}(-1)^n\frac {t^{2n}}{(2n)!}-\sum_0^{\infty} (-1)^n\frac {t^{2n}}{(2n+1)!}}{\sum_0^{\infty} (-1)^n\frac {t^{2n}}{(2n+1)!}}} = \frac t{1 + \frac {\sum_0^{\infty} (-1)^n\frac {2n}{(2n+1)!}t^{2n}}{\sum_0^{\infty} (-1)^n\frac {t^{2n}}{(2n+1)!}}}$

Le terme constant de la série en numérateur est nul, ce qui permet d'écrire :

$\tan t =\frac t{1 + \frac {\sum_1^{\infty} (-1)^n\frac {2n}{(2n+1)!}t^{2n}}{\sum_0^{\infty} (-1)^n\frac {t^{2n}}{(2n+1)!}}} =\frac t{1 + \frac {\sum_0^{\infty} (-1)^{n+1}\frac {2(n+1)}{(2(n+1)+1)!}t^{2(n+1)}}{\sum_0^{\infty} (-1)^n\frac {t^{2n}}{(2n+1)!}}} =\frac t{1 - t^2\cdot \frac {\sum_0^{\infty} (-1)^n\frac {2(n+1)}{(2n+3)!}t^{2n}}{\sum_0^{\infty} (-1)^n\frac {t^{2n}}{(2n+1)!}}}$

On en déduit, si R_k désigne le quotient complet d'indice k de la fraction continue généralisée :

$R_1 = \frac {\sum_0^{\infty}(-1)^n\frac {t^{2n}}{(2n)!}}{\sum_0^{\infty} (-1)^n\frac {t^{2n}}{(2n+1)!}}, \quad R_2 = \frac {\sum_0^{\infty} (-1)^n \cdot \frac 1{(2n+1)!}t^{2n}}{\sum_0^{\infty} (-1)^n \cdot \frac {2(n+1)}{(2n+3)!}t^{2n}} \quad \text{et}\quad \tan{t} = \frac t{R_1} = \frac t{1 - \frac {t^2}{R_2}}$

Montrons par récurrence que :

$R_k = \frac {\sum_0^{\infty} (-1)^n \cdot \frac {2^{k-2}\prod_{j=1}^{k-2}(n+j)}{(2(n+k)-3)!}\cdot t^{2n}}{\sum_0^{\infty} (-1)^n \cdot \frac {2^{k-1}\prod_{j=1}^{k-1}(n+j)} {(2(n+k)-1)!}\cdot t^{2n}}$

Pour k = 2, les calculs précédents établissent la formule. Supposons la vraie pour k et montrons là pour k + 1. Au point t = 0, la valeur de R_k, notée ici a _k est donnée par :

$a_k = \frac {\frac {2^{k-2}\prod_{j=1}^{k-2}j}{(2k-3)!}}{\frac {2^{k-1}\prod_{j=1}^{k-1}j} {(2k-1)!}} = \frac {\frac 1{(2k-3)!}}{\frac{2(k-1)}{(2k-1)!}} = \frac {(2k-1)(2k-2)}{2k-2}= 2k-1$

Ce qui amène le calcul suivant :

$R_k = 2k-1 + \frac {\sum_0^{\infty} (-1)^n \cdot \left(\frac {2^{k-2}\prod_{j=1}^{k-2}(n+j)}{(2(n+k)-3)!}-\frac {(2k-1)2^{k-1}\prod_{j=1}^{k-1}(n+j)} {(2(n+k)-1)!}\right)\cdot t^{2n}}{\sum_0^{\infty} (-1)^n \cdot \frac {2^{k-1}\prod_{j=1}^{k-1}(n+j)} {(2(n+k)-1)!}\cdot t^{2n}}$

En réduisant au même dénominateur :

$R_k = 2k-1 + \frac {\sum_0^{\infty} (-1)^n \cdot \frac{2^{k-2} \prod_{j=1}^{k-2}(n+j)}{(2(n+k)-1)!}\cdot \left((2(n+k)-1)(2(n+k)-2)-2(2k-1)(n+k-1)\right)\cdot t^{2n}} {\sum_0^{\infty} (-1)^n \cdot \frac {2^{k-1}\prod_{j=1}^{k-1}(n+j)} {(2(n+k)-1)!}\cdot t^{2n}}$

En remarquant que le premier terme de la série du numérateur est nul :

$R_k = 2k-1 + \frac {\sum_0^{\infty} (-1)^n \cdot \frac{2^{k-2} \prod_{j=1}^{k-2}(n+j)}{(2(n+k)-1)!}\cdot 4n(n+k-1)\cdot t^{2n}} {\sum_0^{\infty} (-1)^n \cdot \frac {2^{k-1}\prod_{j=1}^k(n+j)} {(2(n+k)-1)!}\cdot t^{2n}} = 2k-1 - t^2\frac {\sum_1^{\infty} (-1)^{n-1} \cdot \frac{2^k \prod_{j=0}^{k-1}(n+j)}{(2(n+k)-1)!}\cdot t^{2(n-1)}} {\sum_0^{\infty} (-1)^n \cdot \frac {2^{k-1}\prod_{j=1}^{k-1}(n+j)} {(2(n+k)-1)!}\cdot t^{2n}}$

En décalant l'indice n du numérateur, on obtient :

$R_k = 2k-1 - \frac{t^2}{\frac {\sum_0^{\infty} (-1)^n \cdot \frac {2^{k-1}\prod_{j=1}^{k-1}(n+j)} {(2(n+k)-1)!}\cdot t^{2n}}{\sum_0^{\infty} (-1)^n \cdot \frac{2^k \prod_{j=1}^k(n+j)}{(2(n+k)+1)!}\cdot t^{2n}}} \quad \text{et}\quad R_k = a_k - \frac {t^2}{R_{k+1}} \quad \text{avec}\quad R_{k+1} = \frac {\sum_0^{\infty} (-1)^n \cdot \frac {2^{(k+1)-2}\prod_{j=1}^{(k+1)-2}(n+j)} {(2(n+k+1)-3)!}\cdot t^{2n}}{\sum_0^{\infty} (-1)^n \cdot \frac{2^{(k+1)-1} \prod_{j=1}^{(k+1)-1}(n+j)}{(2(n+k+1)-1)!}\cdot t^{2n}}$

Fonction exponentielle

Article détaillé : Approximant de Padé de la fonction exponentielle.

Il est possible d'appliquer un algorithme un peu de même manière avec la fonction exponentielle. On peut par exemple, définir les suites suivantes, dont le rapport fournit l'approximation :

$\begin{align} h_0(t) &= 1+ t, & h_1(t) &= 6 + 4t + t^2, & h_2(t) &= 60 + 36t + 9t^2 + t^3 \\ k_0(t) &= 1, & k_1(t) &= 6 - 2t, & k_2(t) &= 60 - 24t + 3t^2\end{align}$

Puis établir la formule de récurrence :

$\forall p \ge 2\quad h_p(t) =(2p+1 + t) h_{p-1}(t) + (2p +1)k_{p-1}(-t) \quad\text{et}\quad k_p(t) =(2p+1 + t) k_{p-1}(t) + (2p +1)h_{p-1}(-t)$

Et en déduire une expression en fraction continue :

$\exp(x) = 1 + x + \frac{\frac 12x^2\mid}{\mid 1-\frac 13x} + \frac{\frac 1{36}x^2 \mid}{\mid 1-\frac 1{15}x} + \frac{\frac 1{100}x^2 \mid}{\mid 1- \frac 1{35}x} + \cdots$

L'algorithme utilisé est ici un peu différent. Les numérateurs ne sont plus des constantes mais des fonctions affines. En revanche une propriété reste commune : le développement limité des fractions h_p / k_p à l'ordre égal à la somme des degrés du numérateur et du dénominateur est identique à celui de la fonction exponentielle.

Il existe de multiples expressions différentes de la fonction exponentielle sous forme de fraction continue. Ce qui amène une série de questions d'ordre général sur les approximations par des fractions rationnelles d'une fonction analytique. Quatre sont particulièrement importantes aux yeux de Padé : pour un couple d'entiers strictement positifs (p, q), existe-t-il une fraction continue h(x) / k(x) tel que h(x) soit un polynôme de degré p, k(x) un polynôme de degré q et tel que la fraction continue ait le même développement limité à l'ordre p + q que la fonction exponentielle ? Existe-t-il des relations de récurrence permettant de passer d'un approximant à un autre à l'aide de formules analogues à celles présentées dans cet exemple ? Ces formules de récurrence permettent-elles d'établir des fractions continues ? Enfin ces fractions continues convergent-elles vers la fonction cible ?

Ces réponses, toutes positives pour la fonction exponentielle, sont l'objet de l'article détaillé. Cet exemple est choisi par Padé^[3] pour introduire sa théorie.

Une démonstration spécifique

La somme des 2p + 2 premiers termes de la série entière k_p(t).e^t est égale à h_p(t) :

Montrons ce résultat pas récurrence sur p. Si p est égal à zéro, on remarque de h₀(t) correspond à l'approximation tangente de l'exponentielle et k₀(t) au polynôme constant un. La proposition est trivialement vérifiée.

Supposons le résultat démontré à l'ordre p - 1, avec la notation de Landau, si ψ_p-1(t) désigne la fonction de R dans R définie par :

$\psi_{p-1} (t) = e^t k_{p-1}(t) - h_{p-1}(t) = \alpha (t^{2p} + \beta t^{2p+1}) + \mathcal O (t^{2p+2}) \quad \alpha, \;\beta \in\mathbb R$

En effet, la fonction ψ_p-1(t) admet manifestement un développement en série entière, car elle est le produit de polynômes et de la fonction exponentielle et l'hypothèse de récurrence montre que sa série commence au terme de puissance 2p. La notation des constantes α et β ainsi séparées n'est pas usuelle, sa raison d'être apparaît dans la suite de la démonstration. Considérons la fonction $ϕ$ _p-1 définie ci-dessous et déterminons son développement limité :

$t \neq 0 \quad \varphi_{p-1}(t) = e^t\frac {\psi_{p-1}(-t)}{\psi_{p-1}(t)} = \left(1 + t + \mathcal O (t^{2})\right)\cdot \frac {t^{2p} - \beta t^{2p+1} + \mathcal O (t^{2p+2})}{t^{2p} + \beta t^{2p+1} + \mathcal O (t^{2p+2})}$

En continuant le calcul, on obtient :

$\varphi_{p-1}(t) = \left(1 + t + \mathcal O (t^{2})\right)\frac {1 - \beta t + \mathcal O (t^{2})}{1 + \beta t + \mathcal O (t^{2})} = \left(1 + t\right)\left(1 - 2\beta t\right)+ \mathcal O (t^{2}) = 1+ (1-2\beta) t +\mathcal O (t^{2})$

On note γ le coefficient (1 - 2β)⁻¹. Remplacer φ_p-1(t) par sa valeur, puis multiplier chaque membre de l'égalité par ψ_p-1(t), et remplacer les occurrences de ψ par leurs expressions, donne les égalités:

$e^t\frac {\psi_{p-1}(-t)}{\psi_{p-1}(t)}= (1 + \gamma^{-1}t)+\mathcal O (t^{2})$ $e^t\Big((1 + \gamma^{-1}t)k_{p-1}(t) + h_{p-1}(-t)\Big) = (1 +\gamma^{-1}t)h_{p-1}(t) + k_{p-1}(-t) +\mathcal O (t^{2p+2})$

Sous réserve de montrer que le coefficient γ est égal à 2p + 1, on obtient ensuite, en reconnaissant l'expression définissant par récurrence les fonctions h_p(t) et k_p(t) :

$e^t\Big((\gamma + t)k_{p-1}(t) + \gamma h_{p-1}(-t) \Big) - \Big((\gamma + t)h_{p-1}(t) + \gamma k_{p-1}(-t) \Big) =e^t k_p(t) - h_p(t)= \mathcal O (t^{2p+2})$

Le développement limité montre la proposition annoncée.

Le coefficient γ est égal à 2p + 1 :

L'algèbre linéaire permet de calculer ce coefficient. La méthode consiste à déterminer la valeur de α à l'aide de la série de coefficients nuls dans le développement en série de e^t.k_p-1(t). On remarque que la fonction h_p(t) est un polynôme de degré p + 1, tous les termes de la série k_p(t).e^t strictement supérieurs à p + 1 et inférieurs ou égal à 2.p + 1 sont nuls, d'après la proposition précédente. Notons a₀, a₁, ... , a_p-1 les coefficients du polynôme k_p-1(t), e₀, e₁, ... , e_j, ... ceux de la série entière e^t et b₀, b₁, ... , b_j, ... ceux de la série entière e^t.k_p-1(t) :

$\begin{align} k_{p-1}(t) &= a_0 + a_1x + \cdots + a_{p-1}x^p \\ e^t &= e_0 + e_1x + \cdots e_jx^j + \cdots \\ e^tk_{p-1}(t) &= c_0 + c_1x + \cdots c_jx^j + \cdots\end{align}$

On note u le vecteur de R^p de coordonnées les coefficients de k_p-1(t) (a₀, a₁,... ,a_p-1), v _k celui de coordonnées b _k+p-1, ... b _k écrit dans l'ordre inverse de telle manière à ce que le coefficient c _k se calcule à l'aide du vecteur v _k dans et <.,.> le produit scalaire canonique de R^p. On obtient les égalités :

$k \ge p+1 \Rightarrow c_k = \langle u, v_k\rangle = \sum_{j=0}^{p-1} a_je_{k-j}\quad\text{avec}\quad v_k = \frac 1{k!} \cdot \left(1, k, k(k-1),\cdots, \prod_{j=0}^{p-2}(k -j) \right)$

Avec ces notations, le paragraphe précédent indique que le vecteur u est orthogonal aux p - 1 vecteurs v_p+1, ..., v_2p-1. Un calcul de déterminant montre que cette famille de p -1 vecteurs est libre, elle forme une base de l'hyperplan de R^p orthogonal de u. Le facteur γ est donné par β, le ratio c_2p+1 / c_2p, les valeurs c_2p+1 et c_2p se calculent à l'aide des vecteurs v_2p+1 et v_2p. Si ces deux vecteurs ne sont pas dans l'orthogonal de u, c_2p+1.v_2p - c_2p.v_2p+1 l'est :

$c_{2p} = \langle u, v_{2p}\rangle, \quad c_{2p+1} = \langle u, v_{2p+1}\rangle \quad \text{et}\quad \langle u,c_{2p+1}v_{2p} - c_{2p}v_{2p+1}\rangle = 0$

Un argument de dimension montre qu'une combinaison linéaire de v_2p et v_2p+1 possède des coefficients proportionnels au couple (c_2p+1, -c_2p) si et seulement si elle est élément de l'hyperplan. Il suffit de trouver une combinaison linéaire de v_2p et v_2p+1 dans l'orthogonal de u pour connaître le ratio c_2p+1 / c_2p et donc β. Autrement dit le calcul de β revient à trouver une combinaison linéaire nulle et non triviale entre les p + 1 vecteurs : v_p+1, ... v_2p+1, le rapport des deux derniers coefficients est égal à l'opposé de β. Dans un premier temps, recherchons une suite (δ_i) de coefficients vérifiant les relations :

$\forall k \in[0,p-1] \quad \sum_{i=0}^p \delta_i\prod_{j=0}^{k-1}(p+i+1-j) = 0$

Le coefficient binomial offre une solution, il suffit de remarquer que :

$\forall k < p \quad \frac {d^k}{dt^k}t^{p+1}(1-t)^p = \frac {d^k}{dt^k}\left(\sum_{i=0}^p (-1)^i \binom{p}{i} t^{p+1+i}\right) = \sum_{i=0}^p (-1)^i \binom{p}{i} \prod_{j=0}^{k-1}(p+1+i-j)t^{p+1+i-k}$

L'égalité précédente, prise au point t = 1 montre le résultat recherché. En termes de combinaison linéaire, on obtient l'égalité :

$\sum_{i=0}^p (-1)^i(p+1+i)! \binom{p}{i} v_{p+1+i} = 0, \quad \langle u, (2p+1)!v_{2p+1} - p(2p)!v_{2p}\rangle =0\quad\text{et}\quad \beta = \frac p{2p+1}$

On en déduit :

$\gamma = \frac 1{1-2\beta} = \frac 1{1 - \frac{2p}{2p+1}}=\frac {2p+1}{2p+1 -2p} = 2p+1$

Convergence du numérateur et du dénominateur :

Ici A désigne un réel strictement positif, p un entier strictement positif et k un entier plus petit ou égal à p. L'objectif est de montrer que si λ_p est l'inverse du coefficient constant de h_p(t) alors λ_p.h_p(t) converge uniformément sur tout intervalle [-A,A] vers la fonction exp(t/2) et λ_p.k_p(t) vers exp(-t/2). Soient a' _p,k et b' _p,k le coefficient du terme d'ordre k du numérateur et du dénominateur de la fraction d'indice p.

On dispose des formules suivantes :

$a'_{p,k} = \frac {(p+1)(2p+1 - k)!}{(p+1-k)!k!}\quad\text{et}\quad b'_{p,k} = (-1)^k\frac {(2p+1-k)!}{(p-k)!k!}$

Démontrons ce résultat par récurrence sur p. On les vérifie manuellement pour p égal à 1. Supposons qu'elles soient vraies à l'ordre p - 1. La formule de récurrence montre que :

$a'_{p,p+1} = 1,\quad a'_{p,p}= (2p+1).1 +a_{p-1,p-1} = 2p+1+p^2=(p+1)^2,\quad b'_{p,p}=(-1)^p(2p+1)+(-1)^{p-1}(p-1)= (-1)^pp$

Et, si k est strictement plus petit que p :

$a'_{p,k}=(2p+1)(a'_{p-1,k} +b'_{p-1,k}) + a_{p-1,k-1}\quad\text{et}\quad b'_{p,k}=(2p+1)(b'_{p-1,k} +(-1)^ka'_{p-1,k}) + b_{p-1,k-1}$

On en déduit :

$a'_{p,k}=(2p+1)\left(\frac {p(2p-1 -k)!}{(p-k)!k!} + \frac {(2p-1-k)!}{(p-1-k)!k!}\right) + \frac {p(2p - k)!}{(p+1-k)!(k-1)!}$

et :

$a'_{p,k}=\frac {(2p-1-k)!}{(p+1-k)!k!}\Big((2p+1)(p+1-k)(2p-k)+pk(2p-k)\Big)=\frac {(2p-k)!}{(p+1-k)!k!}\left((2p+1)(p+1-k)+pk\right) = \frac {(p+1)(2p+1 - k)!}{(p+1-k)!k!}$

Un calcul analogue permet de conclure pour les coefficients de k_p(t).

Pour la suite de la démonstration, a_p,k et b_p,k désignent les k^ième coefficients de λ_p.h_p(t) et λ_p.k_p(t).

Si p tend vers l'infini, a_p,k tend vers 1/(2^k.k!) et b_p,k vers (-1)^k/(2^k.k!) :

On remarque que :

$\lambda_p = (a'_{p,0})^{-1} = \frac {(p+1)!}{(p+1)(2p+1)!} = \frac {p!}{(2p+1)!} \quad\text{et}\quad a_{p,k}= \frac {(p+1)!(2p+1 - k)!}{(p+1-k)!(2p+1)!k!}$

On en déduit :

$a_{p,k} = \frac 1{k!}\prod_{i=0}^{k-1}\frac{p+1-i}{2p+1-i}=\frac 1{2^kk!}\prod_{i=0}^{k-1}\frac{1+\frac{1-i}p}{1+\frac{1-i}{2p}}\quad\text{et}\quad \lim_{p \to \infty} a_{p,k} =\frac 1{2^kk!},\quad 0<a_{p,k}<\frac 1{k!}$

Un calcul analogue établit la propriété pour le dénominateur.

Conclusion :

Sur l'intervalle [-A,A], la série entière de la fonction exp(t) voit son n + 1^ième majoré en valeur absolue par Aⁿ / n!. De plus cette majoration correspond à une série convergente. On en déduit que si ε est un réel strictement positif, il existe un entier N₁ tel que :

$\forall n > N_1 \quad \sum_{k=n}^{\infty} \left|\frac {A^k}{k!}\right| < \frac {\epsilon}3$

Soit n un entier plus grand que N₁ et p un entier plus grand que n :

$\forall t \in [-A,A] \quad \left|h_p(t) - \exp\left(\frac t2\right)\right|\le \left|\sum_{k=0}^n \left(a_{p,k} - \frac 1{2^kk!}\right)t^k\right| + \left|\sum_{k=n}^{p+1} a_{n,k}t^k\right| + \left|\sum_{k=n}^{\infty} \frac{t^k}{2^kk!}\right|$

Les majorations précédentes montrent que :

$\left|\sum_{k=n}^{p+1} a_{n,k}t^k\right| < \sum_{k=n}^{p+1} \frac {A^k}{k!} < \sum_{k=n}^{\infty} \frac {A^k}{k!}< \frac {\epsilon}3\quad\text{et}\quad \left|\sum_{k=n}^{\infty} \frac{t^k}{2^kk!}\right| < \sum_{k=n}^{\infty} \frac {A^k}{k!}< \frac {\epsilon}3$

De plus le calcul de la limite de a_p,k montre l'existence d'un entier P tel que :

$\forall p > P,\; \forall t \in [-A,A] \quad \left|\sum_{k=0}^n \left(a_{p,k} - \frac 1{2^kk!}\right)t^k\right| < \frac {\epsilon}3$

Les deux dernières lignes de calculs établissent que :

$\forall p > P,\; \forall t \in [-A,A] \quad \left|h_p(t) - \exp\left(\frac t2\right)\right|< \frac {\epsilon}3$

Ce qui montre bien la convergence uniforme annoncée. Un calcul analogue montre celle du dénominateur vers exp(-t/2). Le rapport des deux montre la convergence de la fraction rationnelle.

Fragments d'histoire

Origine

Joseph-Louis Lagrange énonce une propriété sur des réduites de fractions continues correspondant à notre définition moderne d'approximant de Padé.

On place parfois^[4] l'origine des approximants de Padé aux travaux d'Euler avec sa démonstration de l'irrationalité de e, la base du logarithme népérien. Il exprime^[5] la fonction exponentielle sous forme de fraction continue. On peut cependant remarquer que le développement d'une réduite correspond à un polynôme et non une fraction rationnelle, cas très particulier d'approximant de Padé. Lambert donne des lettres de noblesse à cette démarche en démontrant que si t un nombre réel non nul est rationnel, alors ni tan(t), ni exp(t) ne l'est (voir à ce sujet l'article Fraction continue), démontrant par là l'irrationalité de π. L'approche reste néanmoins limitée à la recherche d'expressions sous forme de fraction continue de nombres spécifiques, Lambert ne cherche en rien à mieux connaître le comportement d'une fonction.

Joseph-Louis Lagrange (1736-1813) généralise l'emploi des fractions continues à l'analyse. Son optique est plus proche de celle de l'article. La fraction continue d'une fonction est utilisée comme un outil de résolution d'équations différentielles, il est nécessaire de réduire la fraction continue qui s'exprime alors comme une fonction rationnelle et Lagrange remarque que les développements limités de la solution et de la fraction rationnelle coïncident « jusqu'à la puissance de x inclusivement qui est la somme des deux plus hautes puissances de x dans le numérateur et dans le numérateur »^[6], ce qui correspond à une définition moderne des approximants de Padé. Carl Friedrich Gauss (1777-1855) utilise les résultats de Lagrange et généralise l'usage des fractions continues au plan complexe^[7]. La démarche est astucieuse, elle établit la fraction continue d'une fonction que Gauss qualifie de série hypergéométrique et qui lui permet de déterminer des approximants de Padé de nombreuses fonctions comme arctangente ou les fonctions hyperboliques, l'approche reste néanmoins empirique. Rien ne permet de déterminer de manière exhaustive toutes les fractions continues associées à une fonction analytique donnée ou même encore d'ébaucher une classification des fractions continues.

Formalisation

Bernhard Riemann met en évidence un des intérêts des approximants de Padé : ils permettent parfois de prolonger des fonctions analytiques complexes.

Une triple motivation modifie à la fois l'approche et les questions relatives à ces fractions continues un peu spéciales. La première est la conséquence des travaux de Bernhard Riemann (1826-1866). Elles mettent en évidence l'importance de l'analyse complexe, dans cet univers, les fonctions sont souvent définies par des séries entières. Or ces séries ne sont pas convergentes à l'extérieur d'un disque donné, la question du prolongement est parfois cruciale. Les approximants de Padé n'ont pas toujours cette limitation, comme le montre l'exemple de la tangente. Leur étude est naturellement « devenue à l'ordre du jour, de la légitimité de l'emploi, dans le calcul, des séries divergentes^[8] ». Riemann étudie la convergence des fractions continues de Gauss^[9]. Cette convergence est à la base d'une démonstration du théorème d'Apéry, prouvé en 1977 et énonçant que l'image de 3 par la fonction zêta de Riemann est irrationnel^[10].

Charles Hermite (1822 - 1901), le professeur de thèse^[11] de Padé, étudie la question de l'interpolation d'une fonction par une fraction rationnelle ainsi que les propriétés de fractions continues associées à l'exponentielle, ce qui lui permet de montrer la transcendance de e^[12], le premier nombre démontré transcendant qui n'a pas été spécialement conçu pour une démonstration (comme ceux de Liouville). Sur la base de ces idées, Ferdinand von Lindemann (1852-1939) démontre la transcendance de π en 1882 clôturant ainsi la question millénaire de la quadrature du cercle. Ce problème, que Charles Hermite croyait hors de portée et dont il disait : « Je ne me hasarderai point à la recherche d’une démonstration de la transcendance du nombre π. Que d’autres tentent l’entreprise; mais croyez m’en, mon cher ami, il ne laissera pas que de leur en coûter quelques efforts^[13]. » était résoluble avec les techniques qu'il avait développées. Enfin, l'étude de systèmes dynamiques complexes comme ceux étudiés par Henri Poincaré (1854-1912) pour démontrer la statibilité du système solaire impose l'usage de fractions continues de type Padé^[14].

Il est donc naturel que la question des fractions continues, construites à l'aide de fonctions rationnelles, soient à l'ordre du jour à la fin du XIX^e siècle. Cependant, en 1890, Henri Poincaré décrit la théorie des fractions continues algébriques comme une « sorte de terra incognita » dont « la carte est encore presque blanche^[15] ». Henri Padé étudie la question sous un jour nouveau. Il cherche systématiquement la fraction rationnelle dont le numérateur et le dénominateur ont des degrés respectifs ne dépassant pas les valeurs d'un couple (p, q) et qui approxime localement le mieux une fonction analytique donnée. Son travail de thèse^[16], soutenu à l'Université de la Sorbonne en 1892, consiste à étudier la table de ces approximants et à en établir une théorie très générale. Il détermine les lois qui permettent de passer de cette table aux fractions continues, dont il parvient à classifier les représentants importants. En 1898, il applique sa théorie à la fonction exponentielle^[3], indique comment construire toutes les fractions continues régulières de cette fonction. Avant son mémoire, seul 5 exemples étaient connus, son travail montre qu'ils ne correspondent qu'à des cas particuliers d'une triple infinités de fractions.

Une question reste encore largement ouverte, la convergence des différentes fractions continues que l'on peut construire. Thomas Joannes Stieltjes (1856-1895) est d'un apport considérable sur cette question. En 1894, il établit exactement, pour une vaste famille de fractions continues, le domaine de convergence^[17], ce sont celles qui s'avèrent nécessaire pour démontrer la stabilité du système solaire étudiée par Poincaré. Cette question de la convergence est jugé suffisamment importante pour faire l'objet du Grand prix de l'Académie des sciences de Paris de 1906^[18]. Son jury est composé par des grands noms de l'époque comme Poincaré ou Picard. Il est remporté par Padé qui présente « une sorte de synthèse et très large généralisation des résultats que nous venons de rappeler de Thomé, Laguerre et M. de Montessus^[19] ».

Définitions et premières propriétés

Définitions

Dans toute la suite de l'article, f(t) désigne une fonction analytique en 0 et qui ne s'annule pas en 0. Le fait que cette fonction ne s'annule pas en 0 ne limite en rien la généralité des propos. Si g(t) est une fonction analytique en 0, il existe nécessairement une valeur n tel que g(t) soit égal à tⁿ.f(t) où f est une fonction qui satisfait les hypothèses précédentes. Les lettres p et q désignent deux entiers positifs.

Pour Padé, la première question associée à sa théorie est : Existe-t-il une fraction continue h(x) / k(x) telle que h(x) soit un polynôme de degré p, k(x) un polynôme de degré q et telle que la fraction continue ait le même développement limité à l'ordre p + q que f(t) ? Elle amène la définition suivante :

Un approximant de Padé d'indice (p,q) de la fonction f(t) désigne une fraction rationnelle h(t) / k(t) tel que les degrés des polynômes h(t) et k(t) soient inférieurs ou égaux respectivement à p et q et que le développement limité à l'ordre p + q de la fraction soit identique à celui de f(t) en 0^[20].

Si cette définition est souvent reprise, elle n'est pas totalement satisfaisante. Pour s'en rendre compte le plus simple est de considérer le cas où f(t) est égal à 1 + t². Recherchons l'approximation d'indice (1,1), si a + b.t désigne le numérateur, son produit avec la fonction f(t) ne doit pas comporter de terme du deuxième degré, ce qui impose à a d'être nul. Le numérateur doit alors être égal à b.t et on obtient l'égalité suivante :

$bt(1 + t^2) - bt = bt^3\;$

Cependant, une fois les facteurs communs de h(t) et k(t) retranchés, on obtient pour approximant la fonction constante 1. Cet exemple montre qu'il n'existe pas d'approximant de Padé d'indice (1,1). Pour cette raison, une deuxième définition s'avère nécessaire. On ne considère plus une fraction qui approche la fonction f à l'ordre p + q, mais uniquement celle qui approxime le mieux f :

Les termes de fraction réduite ou réduite d'indice (p,q) de la fonction f(t) désignent une fraction rationnelle h(t) / k(t) tel que les degrés des polynômes h(t) et k(t) soient inférieurs ou égaux respectivement à p et q et tel qu'il n'existe aucune fraction rationnelle u(t) / v(t) dont les degrés de u(t) et v(t) soient inférieurs ou égaux respectivement à p et q et tel qu'il existe développement limité de u(t) / v(t) coïncidant avec celui de f(t) à un ordre supérieur au plus grand des ordres des développements limités de h(t) / k(t) coïncidant avec f(t). La réduite d'indice (p,q) est parfois notée f_[p,q](t).

Premières propriétés

La définition de réduite, moins restrictive que celle d'approximant de Padé pallie l'absence de réponse positive à la première question. Les deux définitions sont relativement proches :

Si une fraction rationnelle est une réduite, alors il existe un couple d'indices tel que cette fraction soit un approximant de Padé d'indice ce couple.

Pour l'exemple précédent, la fonction constante 1 est la réduite d'indice (1,1) de la fonction 1 + t². La fonction constante 1 est aussi un approximant de Padé d'indice (0,0), (1,0) ou encore (0,1). Un résultat essentiel à la théorie stipule non seulement de l'existence d'une réduite mais, sous une certaine forme aussi de son unicité :

Pour tout couple (p, q), il existe une réduite h(t) / k(t) d'indice (p, q) de la fonction f(t). Sous réserve d'imposer à h(t) et k(t) d'être premiers entre eux et à k(t) d'avoir un coefficient constant égal à 1, alors h(t) et k(t) sont uniques.^[21]

Les analogies avec la fraction continue sont multiples, ce qui justifie un vocabulaire commun. Certains résultats ressemblent à ceux des fractions continues :

La fonction f(t) est une fraction rationnelle sur un voisinage de 0 si, et seulement si, il existe un couple (m, n) tel que toute réduite d'indice (p, q) tel que p soit plus grand que m et q plus grand que n soit égal à la réduite d'indice (m, n):

Soit u(t) et v(t) deux polynômes de degrés respectifs m et n, si la fraction rationnelle u(t) / v(t) possède le même développement limité à l'ordre m + n que la fonction f(t), alors elle est égale à la réduite d'indice (m, n).

Démonstrations

Construction de la réduite d'indice (p, q) :

Les techniques linéaires utilisées pour l'étude de la fonction exponentielle sont génériques à toute la théorie des approximants. Une réduite h(t) / k(t) correspond à un couple de polynômes tel que l'ensemble des monômes de degré compris entre p + 1 et p + q du développement en série entière de k(t).f(t) soit vide. soit φ(t) le polynôme correspondant au développement limité de f à l'ordre p + q, l'application ψ, qui à un polynôme g(t) de degré inférieur ou égal à q associe φ(t).g(t) est une application linéaire d'un espace vectoriel E de dimension p + 1 dans l'espace de dimension p + 2.q + 1 des polynômes de degré inférieur ou égal à p + 2.q. Soit F le sous espace vectoriel des polynômes de degré inférieur ou égal à p + 2.q composé des éléments ne comportant aucun monôme de degré compris entre p + 1 et p + q, la dimension de F est égal à p + q + 1. La dimension d'un supplémentaire de F, égal à q est strictement plus petite que celle de E, en conséquence ψ ne peut être une bijection entre E et un supplémentaire de F et le sous-espace vectoriel des éléments de E ayant une image dans F par ψ est non réduit au vecteur nul. Soit x^ω.k(t) un polynôme de cet espace dont le monôme de plus petit degré est le plus élevé et de coefficient égal à 1. Soit ω le degré de ce monôme. Le polynôme k(t) est de degré inférieur ou égal à q - ω et de coefficient constant égal à 1.

Soit h₁(t) la restriction au termes de degré inférieur ou égal à p du polynôme φ(t).x^ω.k(t). Le développement limité à l'ordre p + q de x^ω.k(t).f(t) - h₁(t) est nul, par construction, ce qui montre que h₁(t) est un multiple de x^ω (h₁(t) ne peut en effet comporter aucun terme de degré inférieur à ω car x^ω.k(t).f(t) n'en comporte aucun). Soit h(t) le polynôme h₁(t) divisé par x^ω. La fraction rationnelle h(t) / k(t) possède un développement limité à l'ordre p + q - ω égal à celui de f(t).

Existence et unicité de la réduite d'indice (p, q) :

Montrons maintenant que la fraction rationnelle h(t)/k(t) est bien l'unique réduite d'ordre (p, q). Soit u(t) et v(t) deux polynômes premiers entre eux, de degrés respectifs inférieurs à p et q, tel que la constante de v(t) soit égale à 1 et dont le développement limité de u(t) / v(t) à l'ordre p + q - ω coïncide avec celui de f(t). La différence h(t) / k(t) - u(t) / v(t) encore égal à (h(t).v(t) - k(t).u(t)) / k(t).v(t) possède un développement limité nulle à l'ordre p + q - ω. Comme le dénominateur de cette fraction possède une constante égal à 1, son numérateur admet aussi un développement limité nul à l'ordre p + q - ω. Or le numérateur est un polynôme de degré inférieur ou égal à p + q - ω, il est donc nul. Comme h(t) et k(t), ainsi que u(t) et v(t) sont premiers entre eux et que les dénominateurs ont une constante égale à 1, le polynôme h(t) est nécessairement égal à u(t) et k(t) à v(t).

La fraction rationnelle h(t)/k(t) vérifie donc bien la définition d'une réduite d'ordre (p, q) et est unique.

La fonction f(t) est une fraction rationnelle sur un voisinage de 0 si, et seulement si, il existe un couple (m, n) tel que toute réduite d'indice (p, q) tel que p soit plus grand que m et q plus grand que n soit égal à la réduite d'indice (m, n).

Supposons que la fonction f(t) soit une fraction rationnelle et soit u(t) et v(t) deux polynômes de degré respectifs m et n et premiers entre eux, tel que v(t) ait pour constante 1. Soit (p, q) un couple d'indice tel que m ≤ p et n ≤ q. La fraction rationnelle u(t) / v(t) possède toutes les propriétés caractéristique de la réduite d'indice (p, q). Comme cette réduite est unique, elle est nécessairement égale à u(t) / v(t). En conséquence, il existe un couple (m, n) tel que toute réduite d'indice (p, q) tel que p soit plus grand que m et q plus grand que n soit égal à la réduite d'indice (m, n).

Réciproquement, soit f(t) une fonction tel que toute réduite d'indice (p, q) tel que p soit plus grand que m et q plus grand que n soit égal à la réduite d'indice (m, n). Soit u(t) / v(t) la réduite d'indice (m, n). Par hypothèse, f(t) et la fraction rationnelle ont même développement en série entière. Elles sont toutes les deux des fonctions analytiques, elles sont donc confondues sur un voisinage de 0.

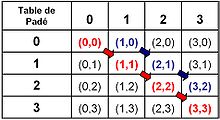
Table de Padé

Une méthode de présentation des approximants est la table de Padé. Elle consiste en un tableau à double entrée dont la case de coordonnées p, q contient la réduite d'indice (p, q). L'article Approximant de Padé de la fonction exponentielle propose celle de l'exponentielle. Dans cet exemple, chaque case contient une fraction rationnelle distincte. Tel n'est pas toujours le cas, comme le montre la table de la fonction Arctangente / t^[22] :

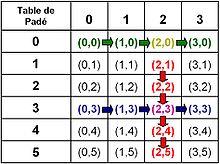
Table de Padé Arctan (t)/t	$\quad 0 \quad$	$1 \;$	$2 \;$	$3 \;$	$4 \;$
$0 \;$	${\color{Blue} 1}\;$	${\color{Blue} 1}\;$	${\color{Red} 1 - \frac 13t^2}$	${\color{Red} 1 - \frac 13t^2}$	${\color{Violet} 1 - \frac 13t^2 + \frac 15t^4}$
$1 \;$	${\color{Blue} 1}\;$	${\color{Blue} 1}\;$	${\color{Red} 1 - \frac 13t^2}$	${\color{Red} 1 - \frac 13t^2}$	${\color{Violet} 1 - \frac 13t^2 + \frac 15t^4}$
$2 \;$	${\color{Maroon} \frac 1{1 + \frac 13t^2}}$	${\color{Maroon} \frac 1{1 + \frac 13t^2}}$	${\color{Plum} \frac {1 + \frac 4{15}t^2}{1 + \frac 9{15}t^2}}$	${\color{Plum} \frac {1 + \frac 4{15}t^2}{1 + \frac 9{15}t^2}}$	${\color{BrickRed} \frac {1 + \frac 8{21}t^2+ \frac 4{105}t^4}{1 + \frac 57t^2}}$
$3 \;$	${\color{Maroon} \frac 1{1 + \frac 13t^2}}$	${\color{Maroon} \frac 1{1 + \frac 13t^2}}$	${\color{Plum} \frac {1 + \frac 4{15}t^2}{1 + \frac 9{15}t^2}}$	${\color{Plum} \frac {1 + \frac 4{15}t^2}{1 + \frac 9{15}t^2}}$	${\color{BrickRed} \frac {1 + \frac 8{21}t^2+ \frac 4{105}t^4}{1 + \frac 57t^2}}$
$4 \quad$	${\color{ForestGreen} \frac 1{1 + \frac 13t^2 -\frac 4{45}t^4}}$	${\color{ForestGreen} \frac 1{1 + \frac 13t^2 -\frac 4{45}t^4}}$	${\color{Black} \frac {1 + \frac {11}{21}t^2}{1 + \frac 6{7}t^2 + \frac 3{35}t^4}}$	${\color{Black} \frac {1 + \frac {11}{21}t^2}{1 + \frac 6{7}t^2 + \frac 3{35}t^4}}$	${\color{Brown} \frac {1 + \frac {7}{9}t^2 + \frac {64}{945}t^4}{1 + \frac {10}{9}t^2 + \frac 5{21}t^4}}$
$5 \quad$	${\color{ForestGreen} \frac 1{1 + \frac 13t^2 -\frac 4{45}t^4}}$	${\color{ForestGreen} \frac 1{1 + \frac 13t^2 -\frac 4{45}t^4}}$	${\color{Black} \frac {1 + \frac {11}{21}t^2}{1 + \frac 6{7}t^2 + \frac 3{35}t^4}}$	${\color{Black} \frac {1 + \frac {11}{21}t^2}{1 + \frac 6{7}t^2 + \frac 3{35}t^4}}$	${\color{Brown} \frac {1 + \frac {7}{9}t^2 + \frac {64}{945}t^4}{1 + \frac {10}{9}t^2 + \frac 5{21}t^4}}$

Ici, les mêmes fractions sont affichées à l'aide une couleur commune. On remarque qu'elles couvrent des surfaces carrées, à l'exception de celles de la colonne 4 car la colonne 5 est manquante. Cette propriété n'est pas spécifique à la fonction arctangente :

Soit h(t) / k(t) la réduite de f(t) une fonction analytique qui n'est pas une fraction rationnelle. Ici, h(t) et k(t) désigne deux polynômes premiers entre eux, de degré respectif p et q et tel que le coefficient constant de k(t) soit égal à 1. Soit ω le plus grand entier tel que le développement limité de la réduite et de f(t) coïncide à l'ordre p + q + ω. L'ensemble des indices associés à la réduite h(t) / k(t) est celui des couples (p + i, q + j) tel que i et j décrivent l'ensemble des entiers compris (au sens large) entre 0 et ω.

Dans le cas où f est une fraction rationnelle le résultat est le même, mais ω peut prendre la valeur infinie.

Démonstration

Ici, le terme de carré désigne la portion de la table ayant pour sommet les quatre cases : (p, q), (p + ω, q), (p, q + ω) et (p + ω, q + ω).

Tout indice du carré possède pour réduite h(t) / k(t) :

Soient i et j deux entiers inférieurs ou égaux à ω, u(t) et v(t) deux polynômes, de degré respectifs inférieurs ou égaux à p + i et q + j, premiers entre eux tel que v(t) ait un terme constant égal à 1 et tel que le développement limité de la fraction u(t) / v(t) soit le même que celui de f(t) au moins à l'ordre p + q + ω. Cette propriété revient à montrer que si u(t) / v(t) approxime aussi bien la fonction f(t) que h(t) / k(t) alors u(t) est égal à h(t) et v(t) à k(t).

La différence des deux fractions, égale à (h(t).v(t) - k(t).u(t)) / k(t).v(t) possède un développement limité à l'ordre p + q + ω nul. Comme le dénominateur possède un terme constant égal à 1, le numérateur possède aussi un développement limité à l'ordre p + q + ω nul. Or c'est un polynôme de degré inférieur ou égal à p + q + ω, ce numérateur est donc nul, ce qui montre l'égalité entre les deux fractions h(t) / k(t) et u(t) / v(t), et donc le résultat.

Aucun indice hors du carré ne possède h(t) / k(t) pour réduite :

Soit (m, n) un indice situé hors du carré. Si m ou n est strictement inférieur respectivement à p ou à q, alors soit le degré de h(t) soit celui de k(t) est trop élevé pour être un candidat et la fraction n'est pas une réduite d'indice (m, n). Supposons que n soit strictement supérieur à q + ω et m au moins égal à p. Le paragraphe précédent montre qu'il existe un entier positif v tel que la réduite d'indice (m, n) soit le quotient de deux polynômes de degré respectifs m - v et n - v et tel que les développements limités du quotient et de f(t) coïncident au moins à l'ordre m + n - v. Raisonnons par l'absurde et supposons que la réduite d'indice (m, n) soit la fraction h(t) / k(t). On dispose alors des égalités :

$p = m - v,\quad q = n-v,\quad p + q + \omega \ge m + n - v \quad\text{et}\quad p + q + \omega \ge p + q + v$

Comme n est strictement supérieur à q + ω, ω est strictement plus petit que v, la dernière majoration est donc impossible. Un raisonnement analogue permet de conclure que si m est strictement plus grand que p + ω, l'indice (m, n) ne possède pas non plus h(t) / k(t) comme réduite, ce qui termine la démonstration.

Fraction continue

Généralités

L'approximant de Padé est particulièrement utile sous forme d'une suite de réduites de plus en plus avancées. Une réduite est dite plus avancée qu'une autre lorsque la somme des degrés du numérateur et du dénominateur de la première est strictement plus élevée que celle de l'autre^[23]. Les résultats précédents montrent qu'une réduite est plus avancée qu'une autre si et seulement si elle représente au voisinage de 0 une meilleure approximation. Ces suites représentent un peu l'équivalent d'une série entière. Une série entière peut être vue comme une suite de polynômes qui approxime localement de mieux en mieux la fonction cible, à l'image des suites d'approximants décrites dans ce paragraphe. Une manière commode de représenter une suite de cette nature est la fraction continue.

Soit (f_{[p_n,q_n]}) une suite d'approximants de Padé de plus en plus avancées. Il existe deux suites de polynômes (α_n) et (β_n) tel que :

$(1)\quad \forall n \in \mathbb N\quad f_{[p_n,q_n]} = \alpha_0 + \frac{\alpha_1\mid}{\mid \beta_1} + \frac{\alpha_2\mid}{\mid \beta_2} + \cdots + \frac{\alpha_n\mid}{\mid \beta_n}$

Ici, l'égalité doit être prise au sens algébrique du terme. Cela signifie par exemple que la fraction (x - 1) / (x - 1) est égal à 1. En termes de fonction rationnelle, l'égalité n'est pas tout à fait exacte, la première fonction n'est pas définie en 1 alors que la seconde l'est. Cette situation est illustrée par l'exemple suivant : La fraction continue n'est pas définie au point t = 0, alors que son expression réduite l'est et vaut 0 :

$\frac{1+t\mid}{\mid 1} + \frac{1+t\mid}{\mid 1} - \frac{1+t\mid}{\mid 1} = -t(1+t)$

L'intérêt d'une écriture sous forme de fraction continue réside dans le fait que la suite s'exprime par une relation de récurrence. Les suites de polynômes peuvent être définies par :

$\begin{align} \alpha_0 &= h_{(p_0,0)}, & \alpha_1 &= h_{(p_1,q_1)} - h_{(p_0,0)}\cdot k_{(p_1,q_1)}, & \alpha_{n+2} &= k_{(p_{n+2},q_{n+2})}\cdot h_{(p_{n+1},q_{n+1})} - h_{(p_{n+2},q_{n+2})}\cdot k_{(p_{n+1},q_{n+1})} \\ \beta_0 &= 1, & \beta_1 &= k_{(p_1,q_1)}, & \beta_{n+2} &= h_{(p_{n+2},q_{n+2})}\cdot k_{(p_n,q_n)} - k_{(p_{n+2},q_{n+2})}\cdot h_{(p_n,q_n)} \end{align}$

Ces relations de récurrence permettent d'exprimer les réduites :

$\begin{align} h_0 &= \alpha_0, & h_1 &=\alpha_0\cdot \beta_1 + \alpha_1, & h_{n+2} &= \alpha_{n+2}\cdot h_n + \beta_{n+2}\cdot h_{n+1} \\ k_0 &= \beta_0, & k_1 &=\beta_1 , & k_{n+2} &= \alpha_{n+2}\cdot k_n + \beta_{n+2}\cdot k_{n+1} \end{align}$

Cette démarche est possible avec toute suite de fractions rationnelles, à condition que la suite de réduites ne soit composée que de fraction distinctes. Elle possède néanmoins une faiblesse, les expressions du numérateur et du dénominateur établies par la formule de récurrence n'ont aucune raison d'être premières entre elles, ainsi h_n est un multiple de h_{[p_n,q_n]} mais ces deux expressions n'ont pas de raison d'être égales. En terme algébrique, on ne dispose que de l'égalité h_{[p_n,q_n]} / k_{[p_n,q_n]} = h_n / k_n. Le numérateur et le dénominateur sont multipliés par un polynôme parasite. Il complexifie inutilement l'expression de la réduite et, pour un calcul effectif, ajoute une instabilité par l'adjonction de singularités factices.

Les calculs pour établir les différentes expressions de ce paragraphe sont les mêmes que ceux utilisées dans l'article Fraction continue.

Remarque : L'expression (1) exprime le fait que le premier terme α₀ est un polynôme. Si ce terme n'est pas nul, dans une suite d'approximants de Padé, il correspond nécessairement à une expression du type h_[p,0]. Toute fois, il existe des fractions continues de la forme :

$\frac{\alpha_1\mid}{\mid \beta_1} + \frac{\alpha_2\mid}{\mid \beta_2} + \cdots + \frac{\alpha_n\mid}{\mid \beta_n}$

Pour tenir compte de cette éventualité, on autorise, dans cet article le choix d'un terme α₀ nul dans les suites d'approximants de Padé. Les mêmes formules s'appliquent et uniquement le premier terme, celui d'indice 0, n'est pas nécessairement un approximant de Padé, mais peut aussi être nul.

Fraction continue simple

Il est possible d'établir des relations de récurrence qui assurent que les expressions du numérateur et du dénominateur des réduites soient premières entre elles et interdisent l'apparition du polynôme parasite décrit au paragraphe précédent. Pour cela, il est utile d'établir une définition :

Une fraction continue est dite simple lorsque la suite des polynômes (α_n), si n est supérieur ou égal à 1, est composée de monômes dont ni l'exposant ni le coefficient ne sont nuls et tel que la suite (β_n) est composée de polynômes dont les constantes ne sont pas nulles.

Cette condition est un peu équivalente à celle qui sépare les fractions continues de nombres réels, dont les numérateurs partiels sont toujours égaux à 1 d'avec les fractions continues généralisées qui ont des numérateurs partiels quelconques. À l'image de la situation des fractions continues de nombres réels, on dispose de la propriété recherchée pour les numérateurs et les dénominateurs des réduites :

Si les expressions des réduites h₁ et k₁ d'une fraction continue simple ont une constante non nulle et sont premières entre elles, alors pour tout n strictement positif, les polynômes h_n et k_n ont des constantes non nulles et sont premiers entre eux.

Établir une expression utilisable d'une suite d'approximants de Padé sous forme de fraction continue est ainsi simplifié si la suite recherchée est une fraction simple. Il est indispensable de disposer d'une condition nécessaire et suffisante pour déterminer quelles suites génèrent des fractions simples.

Soit une suite d'approximants de Padé f_{[p_n,q_n]} telle que les deux suites (p_n) et (p_n) soient croissantes et la suite (p_n+p_n) strictement croissante. La suite d'approximants forme une fraction continue simple si, et seulement si, les polynômes suivants sont des monômes :

$\forall n \in \mathbb N,\; \exists a_n \in \mathbb R^*,\; \exist d_n \in \mathbb N^* \quad h_{(p_n,q_n)}\cdot k_{(p_{n+1},q_{n+1})} - h_{(p_{n+1},q_{n+1})}\cdot k_{(p_n,q_n)} = a_nx^{d_n}$

Dans ce cas, les expressions des suites de polynômes (α_n) et (β_n) sont données par les formules suivantes :

$\begin{align} \alpha_0 &= f_{[p_0,0]}, &\alpha_1 &= h_{(p_1,q_1)} - f_{[p_0,0]}\cdot k_{(p_1,q_1)}, & \alpha_{n+2} &= \frac {k_{(p_{n+2},q_{n+2})}\cdot h_{(p_{n+1},q_{n+1})} - h_{(p_{n+2},q_{n+2})}\cdot k_{(p_{n+1},q_{n+1})}}{h_{(p_{n+1},q_{n+1})}\cdot k_{(p_n,q_n)} - k_{(p_{n+1},q_{n+1})}\cdot h_{(p_n,q_n)}} \\ \beta_0 &= 1, & \beta_1 &= k_{(p_1,q_1)}, & \beta_{n+2} &= \frac {h_{(p_{n+2},q_{n+2})}\cdot k_{(p_n,q_n)} - k_{(p_{n+2},q_{n+2})}\cdot h_{(p_n,q_n)}}{h_{(p_{n+1},q_{n+1})}\cdot k_{(p_n,q_n)} - k_{(p_{n+1},q_{n+1})}\cdot h_{(p_n,q_n)}}\end{align}$

L'égalité stricte entre h_n et h_{[p_n,q_n]}, puis entre k_n et k_{[p_n,q_n]} est alors garantie. Si la fraction continue recherchée ne contient pas de terme polynomial initial, il est toujours possible de fixer la condition α₀ égal à 0.

$Padé fraction continue simple.jpg$

Il reste encore à trouver un moyen pratique pour construire une suite de réduites satisfaisant la proposition précédente. La connaissance de la structure de la table de Padé permet de répondre à ce besoin. Elle est composée de carrés ne contenant que des réduites égales. De manière formelle, soient p, q et ω trois entiers positifs tels que les couples (p, q), (p+ω, q), (p, q+ω) et (p+ω, q+ω) forment les sommets du carré contenant toutes les occurrences de l'approximant de Padé f_{[p, q]}. C'est-à-dire que la fraction formée par les polynômes h_{[p, q]} et k_{[p, q]} de degrés respectifs p et q approxime la fonction f exactement à l'ordre p + q + ω. La propriété suivante permet de trouver les candidats pour la construction d'une fraction continue simple :

Les deux polynômes suivants sont des monômes :

$h_{(p,q)}\cdot k_{(p+\omega + 1,q)} - h_{(p+\omega + 1,q)}\cdot k_{(p,q)},\quad h_{(p,q)}\cdot k_{(p,q+\omega + 1)} - h_{(p,q+\omega + 1)}\cdot k_{(p,q)}$

Si ω est égal à 0, le polynôme suivant est un monôme :

$h_{(p,q)}\cdot k_{(p+1,q+1)} - h_{(p+1,q+1)}\cdot k_{(p,q)}$

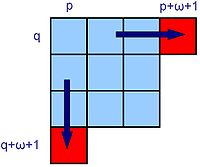
La figure de droite illustre cette situation. Toutes les cases du carré bleu contiennent la même réduite. Si l'une de ses cases est un élément de la suite des approximants de Padé et si la suivante est l'une des deux cases rouges, le numérateur partiel de la fraction continue est un monôme non nul et le dénominateur un polynôme de constante non nulle. Dans le cas où le carré se réduit à une unique case, il est aussi possible de choisir la case diagonale en bas à droite.

Démonstrations

Démontrons tout d'abord un lemme, utile pour plusieurs démonstrations. Il est analogue à la situation que l'on trouve avec les nombres réels :

L'expression suivante est un monôme non nul :

$\forall n \in \mathbb N^*,\; \exists c_n \in \mathbb R^*,\; \exist \mu_n \in \mathbb N^* \quad h_n\cdot k_{n-1} - k_n\cdot h_{n-1} = c_n\cdot t^{\mu_n}$

On raisonne par récurrence. Si n est égal à 1, l'égalité suivante montre le résultat :

$h_1\cdot k_0 - k_1\cdot h_0 = h_1 - k_1\cdot h_0 = \alpha_1$

On suppose la propriété vraie à l'ordre n - 1. En remplaçant h_n et k_n par leurs expressions fournies par la formule de récurrence, on obtient :

$h_n\cdot k_{n-1} - k_n\cdot h_{n-1} = \Big(\alpha_n\cdot h_{n-2} + \beta_n\cdot h_{n-1}\Big)\cdot k_{n-1} - \Big(\alpha_n\cdot k_{n-2} + \beta_n\cdot k_{n-1}\Big)\cdot h_{n-1} = \alpha_n \cdot \Big(h_{n-2}\cdot k_{n-1} - k_{n-2}\cdot h_{n-1}\big) = -c_{n-1}\cdot \alpha_n\cdot t^{\mu_n}$

Ce qui est bien un monôme non nul car par hypothèse de récurrence c_n est non nul et α_n est aussi un monôme non nul. La propriété est vraie à l'ordre n, ce qui termine la démonstration.

Si h₁ et k₁ ont une constante non nul et sont premiers entre eux, alors pour tout n, h_n et k_n ont une constante non nul et sont premiers entre eux.

Démontrons cette proposition par récurrence sur n. Par hypothèse, elle est vraie si n est égal 1. Supposons qu'elle soit vraie à l'ordre n - 1, et montrons là pour n. On dispose de l'égalité :

$h_n = \alpha_n\cdot h_{n-2} + \beta_n\cdot h_{n-1} \quad\text{et}\quad k_n = \alpha_n\cdot k_{n-2} + \beta_n\cdot k_{n-1}$

Au point 0, α_n est nul, mais ni β_n h_n-1, k_n-1 ne le sont, ce qui montre que les constantes de h_n et k_n ne sont pas nuls.

Le lemme et l'identité de Bézout montrent qu'un diviseur de h_n et k_n est un diviseur du monôme c_n.t ^μ_n donc de t. Or on vient de montrer que t n'est ni un diviseur de h_n ni de k_n, ce qui montre que ces deux polynômes sont premiers entre eux.

Si la suite d'approximants de Padé f_{[p_n,q_n]} forme une fraction continue simple, alors les polynôme suivants sont des monômes :

$\forall n \in \mathbb N,\; \exists a_n \in \mathbb R^*,\; \exist d_n \in \mathbb N^* \quad h_{(p_n,q_n)}\cdot k_{(p_{n+1},q_{n+1})} - h_{(p_{n+1},q_{n+1})}\cdot k_{(p_n,q_n)} = a_nx^{d_n}$

Montrons par récurrence que l'expression est bien un monôme. Si n est égal à 0, On a l'égalité :

$h_{(p_0,0)}\cdot k_{(p_{1},q_{1})} - h_{(p_{1},q_{1})}\cdot k_{(p_{0},q_{0})} = h_{(p_0,0)}\cdot k_{(p_{1},q_{1})} - h_{(p_{1},q_{1})} =\alpha_1$

Qui est bien un monôme car si la fraction continue est simple, α₁ est un monôme. Si α₀ égal à 0, l'expression est égale à h_[p₁,q₁], encore égal à α₁ qui est toujours un monôme.

Supposons la propriété vraie à l'ordre n - 1. Les formules de récurrence montre que :

$\begin{align} h_{(p_{n+1},q_{n+1})} &= \alpha_{n+1}\cdot h_{(p_{n-1},q_{n-1})} + \beta_{n+1}\cdot h_{(p_n,q_n)} &\quad\text{et}\quad h_{(p_{n+1},q_{n+1})}\cdot k_{(p_n,q_n)} &= \alpha_{n+1}\cdot h_{(p_{n-1},q_{n-1})}\cdot k_{(p_n,q_n)} + \beta_{n+1}\cdot h_{(p_n,q_n)}\cdot k_{(p_n,q_n)} \\ k_{(p_{n+1},q_{n+1})} &= \alpha_{n+1}\cdot k_{(p_{n-1},q_{n-1})} + \beta_{n+1}\cdot k_{(p_n,q_n)} &\quad\text{et}\quad k_{(p_{n+1},q_{n+1})}\cdot h_{(p_n,q_n)} &= \alpha_{n+1}\cdot k_{(p_{n-1},q_{n-1})}\cdot h_{(p_n,q_n)} + \beta_{n+1}\cdot k_{(p_n,q_n)}\cdot h_{(p_n,q_n)} \end{align}$

Par soustraction des deux dernières égalités on obtient :

$h_{(p_{n+1},q_{n+1})}\cdot k_{(p_n,q_n)} - k_{(p_{n+1},q_{n+1})}\cdot h_{(p_n,q_n)} = \alpha_{n+1}\Big(h_{(p_{n-1},q_{n-1})}\cdot k_{(p_n,q_n)}- k_{(p_{n-1},q_{n-1})} \cdot h_{(p_n,q_n)}\Big)$

L'hypothèse de récurrence ansi que le fait que α_n+1 soit un monôme montre que l'expression à l'ordre n est bien un monôme.

Si les polynômes précédents sont des monômes alors la fraction continue associée à la suite d'approximants de Padé est simple :

Il est immédiat de vérifier que le coefficient α₁ est bien un monôme non nul de degré strictement positif. Le calcul de la démonstration précédente montre l'égalité :

$\forall n \in \mathbb N\quad \alpha_{n+2} = \frac {k_{(p_{n+2},q_{n+2})}\cdot h_{(p_{n+1},q_{n+1})} - h_{(p_{n+2},q_{n+2})}\cdot k_{(p_{n+1},q_{n+1})}}{h_{(p_{n+1},q_{n+1})}\cdot k_{(p_n,q_n)} - k_{(p_{n+1},q_{n+1})}\cdot h_{(p_n,q_n)}}$

Comme les avancements des approximants de Padé des trois indices n, n + 1 et n + 2 sont strictement croissants, ni le numérateur ni le dénominateur ne peuvent être nul. Montrons que cette fraction est un polynôme. Le numérateur s'écrit :

$k_{(p_{n+1},q_{n+1})}\Big(k_{(p_{n+2},q_{n+2})}\cdot f - h_{(p_{n+2},q_{n+2})}\Big) - k_{(p_{n+2},q_{n+2})}\Big(k_{(p_{n+1},q_{n+1})}\cdot f - h_{(p_{n+1},q_{n+1})}\Big)$

Cherchons le monôme de plus petit degré de chacune des deux séries entières de la différence précédente. Celui de gauche est le produit d'un polynôme de constante différente de 0 et d'une série entière de premier terme de degré au moins égal à p_n+2 + q_n+2 + 1, son monôme de plus petit degré est au moins égal à p_n+2 + q_n+2 + 1. Le même raisonnement sur le terme de droite montre que le mônome de plus petit degré est ici au moins égal à p_n+1 + q_n+1 + 1. Comme l'approximant de Padé d'indice n + 2 est plus avancée que celui d'indice n + 1, le monôme de plus bas degré est au moins égal à p_n+1 + q_n+1 + 1. Or le dénominateur est par hypothèse un monôme et son degré ne peut dépasser le maximum entre les deux valeurs p_n+1 + q_n et p_n + q_n+1, qui sont strictement plus petites que le degré du monôme de plus bas degré du numérateur. Enfin, le degré du numérateur de α_n+2 est au plus égal à p_n+2 + q_n+2 + 1, le degré de son monôme de plus bas degré, ce qui montre que le numérateur est un monôme. La fraction α_n+2 s'exprime comme le rapport de deux monômes, ce qui montre qu'elle correspond à un monôme.

Le même raisonnement montre que β_n+2 est bien un polynôme non nul. Si sa constante était nulle, alors h_{[p_n+2,q_n+2]} serait un multiple de t, ainsi que k_{[p_n+2,q_n+2]} ces polynômes ne seraient pas premiers entre eux, ce qui est impossible pour un approximant de Padé.

Les deux polynômes suivants sont des monômes :

$h_{(p,q)}\cdot k_{(p+\omega + 1,q)} - h_{(p+\omega + 1,q)}\cdot k_{(p,q)},\quad h_{(p,q)}\cdot k_{(p,q+\omega + 1)} - h_{(p,q+\omega + 1)}\cdot k_{(p,q)}$

Le raisonnement est analogue au précédent. Démontrons la proposition pour le premier polynôme. Son monôme dominant est de degré p + q + ω + 1. Il s'exprime aussi comme la différence des deux séries entières suivantes :

$k_{(p,q)}\Big(k_{(p+\omega+1,q)}\cdot f - h_{(p+\omega+1,q)}\Big) - k_{(p+\omega+1,q)}\Big(k_{(p,q)}\cdot f - h_{(p,q)}\Big)$

Ce qui montre que son monôme de plus petit degré est de même valeur. Comme ce polynôme ne peut être nul car les fractions d'indices (p, q) et (p + q + ω + 1, q) sont distinctes, le polynôme est nécessairement un monôme non nul.

Fraction continue régulière

Même en imposant à la fraction continue d'être simple, il reste encore un très vaste choix de suites d'approximants disponibles. Il suffit de sauter d'un carré au carré adjacent situé soit en bas soit à droite. À partir d'une case initiale, situé sur un bord, deux choix au moins se présentent à chaque étape et trois si la largeur du carré est égal à 1. Une nouvelle contrainte peut encore simplifier massivement les calculs :

Une fraction simple est dite régulière lorsque, à partir du deuxième indice, les suites de polynômes (α_n) et (β_n) sont de même degrés.

Une telle recherche prend tout son sens si les carrés de même réduites de la table de Padé présentent une géométrie régulière. Étudions le cas où ω, la longueur du côté d'un carré quelconque, est toujours égal à 1. Trois déplacements sont possibles : vers le bas, la droite ou en diagonale, en bas à droite, pour assurer la simplicité. Ajouter la régularité impose un déplacement précis. Il en existe de trois types différents et pour tous ces types, le démarrage de la suite se situe sur une case au bord de la table, c'est-à-dire à partir d'une réduite d'indice (p, 0) ou (0, q).

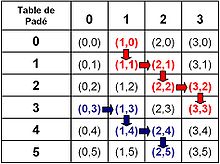
Fraction continue régulière de type I

Fraction continue régulière de type II

Pour le premier type, on démarre soit par une descente, soit par un déplacement à droite, puis la suite suit une trajectoire en escalier, illustrée sur la figure de gauche et composée d'une alternance régulière de déplacements une fois vers la droite puis une fois vers le bas. La fraction continue est composée d'un numérateur réduit à un monôme du premier degré et d'un dénominateur égal une constante. Par exemple, pour la fonction exponentielle, Lagrange démarre par la réduite d'indice (1, 0) et obtient, en suivant la trajectoire illustrée en rouge, le résultat suivant :

$\exp(t) = 1 + \frac{t\mid}{\mid 1} - \frac{\frac 12 t \mid}{\mid 1} + \frac{\frac 16t \mid}{\mid 1} - \frac{\frac 16t \mid}{\mid 1} + \frac{\frac 1{10}t \mid}{\mid 1} - \frac{\frac 1{10}t \mid}{\mid 1} + \frac{\frac 1{14}t \mid}{\mid 1} - \frac{\frac 1{14}t \mid}{\mid 1}+\cdots$

Le type II correspond à la figure de droite. Il suppose un déplacement constant soit vers le bas, soit vers la droite. Le numérateur est toujours un monôme de degré 1, mais cette fois, le dénominateur est un polynôme de degré 1. La première fraction continue historique, constituée par des approximants de Padé est de cette nature. Elle est l'œuvre d'Euler et prend la forme suivante :

$\exp(t) = \frac{1\mid}{\mid 1} - \frac{t \mid}{\mid 1+t} - \frac{\frac 12t \mid}{\mid 1+ \frac 12t} - \frac{\frac 13t \mid}{\mid 1+\frac 13 t} - \frac{\frac 14t \mid}{\mid 1+\frac 14t} - \cdots$

Elle représente la suite illustrée en vert. Les réduites ont pour numérateur les différents développements limités de la fonction exponentielle et pour dénominateur 1. Pour cette raison, on a longtemps cru que ce type de fraction continue n'était qu'une exception^[24]. Il existe pourtant une infinité de fractions continues de cette nature, pour chaque fonction analytique, sous reserve que chaque carré soit de côté 1. Il suffit de choisir une case quelconque situé au bord de la table, puis de se déplacer d'un cran à chaque étape, soit vers la droite si la case initiale correspond à une fraction, soit vers le bas si elle correspond à un polynôme.

Fraction continue régulière de type III

Le troisième type est celui utilisé comme exemple dans cet article pour la fonction exponentielle. Le numérateur est un monôme de degré 2 et le dénominateur un polynôme de degré 2. Un exemple est donné par une fonction issue du logarithme :

$\log \frac{1+t}{1-t} = \frac{2t\mid}{\mid 1} - \frac{\frac 13 t^2 \mid}{\mid 1+\frac 13 t^2} - \frac{\frac 35t^2 \mid}{\mid 1+ \frac 35t^2} - \frac{\frac 57 t^2 \mid}{\mid 1+\frac 57 t^2} - \frac{\frac 79t^2 \mid}{\mid 1+\frac 79t^2} - \cdots$

Il existe une exception possible à ce type. Il arrive que le monôme dominant dénominateur se simplifie systèmatiquement, ce qui est le cas pour l'exemple donné à propos de la fonction tangente. La tangente est aussi différente car les carrés de la table de Padé ont un côté de longueur 2 et non 1. Cette nouvelle géométrie engendre des relations de récurrence différentes. Pour l'exemple choisi, les déplacements forment une progression en escalier, on trouve les points (1,0), (1,2), (3,2) ... Avec des côtés de longueur 2.

Les démonstrations associées à ce paragraphe se trouvent dans l'article Approximant de Padé de la fonction exponentielle. Si l'article traite exclusivement d'une fonction particulière, la logique décrite est générale aux tables de Padé régulières dont les carrés sont tous de côtés 1. Le raisonnement se généralise simplement pour les tables régulières dont les carrés sont de côtés 2.

L'approche consistant à construire la fraction continue à l'aide d'une relation de récurrence est plus simple que celle des divisions successives, par inversion de séries entières comme le faisait Lambert, méthode que Padé qualifie de fort pénible^[25].

Convergence

Structure du domaine

L'un des attraits de l'approximant de Padé est sa capacité à avaler les pôles d'une fonction analytique. La question de la convergence est, en conséquence, particulièrement cruciale. Elle est néanmoins difficile. Ce paragraphe se limite à présenter une méthode^[26] permettant de mettre en valeur un élément structurel du domaine de convergence, dans le cas d'une fraction continue simple.

Une technique analogue à celle utilisée pour les fractions continues fournit l'égalité :

$\forall n \in \mathbb N \quad \frac {h_{(p_{n+1},q_{n+1})}(t)} {k_{(p_{n+1},q_{n+1})}(t)} - \frac {h_{(p_{n},q_{n})}(t)} {k_{(p_{n},q_{n})}(t)} = \frac{(-1)^n \prod_{k=1}^{n+1} \alpha_k(t)}{k_{(p_{n+1},q_{n+1})}(t)\cdot k_{(p_{n},q_{n})}(t)}$

Le numérateur du terme de droite est un monôme dont les puissances sont croissantes avec n, on peut l'écrire a_{ν_n+1}.t ^ν_n+1. Le dénominateur est une suite de polynômes que l'on note d_n+1(t). Avec ces notations, on en déduit l'expression :

$f_{[p_n,q_n]}(t) = h_{(p_0,0)}(t) + \left(f_{[p_{1},q_{1}]}(t) - f_{[p_{0},0]}(t)\right) + \cdots + \left( f_{[p_{n},q_{n}]}(t) - f_{[p_{n-1},q_{n-1}]}(t)\right)= h_{(p_0,0)}(t) +\sum_{i=1}^n \frac {a_{\nu_n}}{d_n(t)}t^{\nu_n}$

On obtient une expression de la n^ième réduite sous forme d'une série entière dont chaque terme est divisé par un élément d'une suite de polynômes. Supposons que la suite de polynômes (k_{[p_n,q_n]}) converge uniformément vers une fonction nécessairement continue k, soit H son domaine de convergence oté des racines de k et D le disque de convergence de la série entière de terme général a _k.t ^k (soit il existe une valeur n tel que k soit égal à ν_n+1 et a _k est égal à a_{ν_n+1} soit il n'y en a pas et a _k est défini comme nul).

Sur l'intersection de D et de H, la fraction continue converge. Ainsi, si un pôle a été attrapé par la suite de polynômes (k_{[p_n,q_n]}) il est devient un racine de k. La fraction continue est à même d'avaler ce pôle s'il est contenu dans le disque D. Par défaut, il n'existe aucune raison pour que la série entière de terme général a _k.t ^k ait le même rayon de convergence que celui du développement en 0 de la fonction analytique f(t). Il est logique que les pôles de la fonction analytique ne représente plus une barrière infranchissable pour la fraction continue.

Illustration par l'exemple de la fonction tangente

Modifions un peu les conventions utilisées précédemment pour assurer un dénominateur de constante égale à 1 :

$\forall n \ge 2\quad h_n(t) = h_{n-1}(t) -\frac {t^2}{(2n-1)(2n-3)}h_{n-2}(t) \quad \text{et}\quad k_n(t) = k_{n-1}(t) -\frac {t^2} {(2n-1)(2n-3)} k_{n-2}(t)$

Les fractions sont les mêmes à un facteur multiplicatif du numérateur et du dénominateur, qui ne modifie donc pas ses valeurs. Elles sont maintenant normalisées. Avec les notations du paragraphe précédent, on a :

$\forall n \in \mathbb N \quad a_{2n} = \left( \prod_{i=1}^n \frac 1{2i-1} \right)t^{2n}\quad\text{et}\quad a_{2n+1} = 0$

Il suffit de remarquer que i est majoré par 2i - 1 pour conclure que cette série est majorée par le développement en série de exp(t²), la série considérée ici est en conséquence uniformément convergente sur tout bornée de C (l'ensemble des nombres complexes) et converge sur C tout entier.

La suite des dénominateurs de la fraction continue converge manifestement vers la fonction cosinus.

Il suffit alors de vérifier que la suite des dénominateurs n'a pas tendance à se rapprocher de zéro en dehors des pôles de la fonction tangente. Le graphique ci-dessus laisse supposer que cette suite converge bien vers la fonction cosinus. Un calcul plus subtil permet de vérifier que cette convergence a lieu sur tout le plan complexe et est uniforme sur tout compact. La suite (v_n(t)) converge donc vers son carré.

Soit R un nombre réel strictement positif choisi le plus grand possible et ε un nombre réel positif choisi le plus petit possible. Soit D le domaine égal au disque fermé de rayon R auquel on a retranché les disques ouverts de centre (2.j+1).π / 2, ici j est un indice décrivant l'ensemble des entiers. Sur D la suite des approximants de Padé est normalement convergente. Il suffit, pour s'en convaincre de remarquer que la fonction cos(t)² n'a pas de racine sur le compact D et qu'elle est continue, en conséquence il existe une constante strictement positive 2.c tel que le module de cos(t)² soit toujours supérieur à 2.c. Il existe un rang N tel que toute fonction de la suite (v_n(t)) d'indice supérieur à N est, en module, supérieur à c sur D. Il suffit alors d'appliquer le raisonnement du paragraphe précédent en remplaçant le couple (p₀, 0) par (p_N, q_N).

Ce raisonnement montre que la série est majorée par celle de terme général 1/c. a_2nR²ⁿ qui est convergente.

Démonstration

Si le raisonnement est relativement simple, au sens où il ne fait preuve d'aucune imagination, la richesse des indices rend la lecture un peu laborieuse. La technique utilisée ici consiste à déterminer la suite des coefficients des polynômes du dénominateur. La méthode usuelle utilise le calcul différentiel^[27]. Elle n'est pas choisie ici car elle n'illustre pas le caractère structurel du domaine de convergence à l'aide de la logique de Padé et ne montre que la convergence de la fraction continue vers la fonction tangente et non celle spécifique de son dénominateur.

On utilise la notation suivante, licite car le polynôme est paire et que les signes des coefficients s'alternent :

$\forall n \in \mathbb N\quad k_{2n}(t) = \sum_{i=0}^{n} (-1)^i b_{2n,2i}t^{2i}\quad\text{et}\quad k_{2n+1}(t) = \sum_{i=0}^{n} (-1)^i b_{2n+1,2i}t^{2i}$

Le fait d'avoir extrait le signe du coefficient permet une petite simplification de la relation de récurrence, un signe moins devient plus :

$b_{0,0} = b_{n,0} = 1 \quad\text{et}\quad \forall n \ge 2,\;\forall i\le n\quad b_{n,2i} = b_{n-1,2i} + \frac {b_{n-2,2i-2}}{(2n-1)(2n-3)}$

En utilisant à nouveau la formule de récurrence sur b_n-1,2i, puis en réitérant, on obtient :

$(1)\quad b_{n,2i} = b_{n-2,2i} + \frac {b_{n-3,2i-2}}{(2n-5)(2n-7)} + \frac {b_{n-2,2i-2}}{(2n-1)(2n-3)}= \cdots =\sum_{j=0}^{n-2i}\frac {b_{n-j-2,2i-2}}{(2n-2j-1)(2n-2j-3)}$

On connaît la valeur des coefficients si i est égal à 0, ils sont tous égaux à 1. La formule précédente permet de calculer l'expression des coefficients pour i égal à 2, puis à 4 etc... Cette technique est utilisée ici et fournit la formule suivante :

$(2)\quad \forall n \ge 2i\quad b_{n,2i} = \frac 1{(2i)!}+ \sum_{k=1}^i \left( \frac {(-1)^k}{(2(i-k))!k!2^k}\prod_{l=1}^k\frac 1{2(n-l)+1} \right)$

On procède par récurrence. Pour i égal à 0, la relation est triviale, car les constantes de tous les polynômes sont égales à 1.

Formule pour i = 1 :

Imposer 1 comme valeur de i dans la formule (2) simplifie bien les chose. Elle devient :

$\forall n \ge 2\quad b_{n,2} = \frac 12 - \frac 1{2(2n -1)}$

La formule (1) montre que :

$b_{n,2i} = \frac 1{1\times 3} + \frac 1{3\times 5} + \cdots +\frac 1{(2n-1)(2n-3)}= \frac 12\left(1 - \frac 13 -\frac 13 + \frac 15 -\cdots + \frac 1{2n-3} -\frac 1{2n-1}\right)$

Pour obtenir ce résultat, chaque terme de la série est égalé à deux termes de signes alternés et qui s'annulent entre eux deux à deux : 1/1x3 = 1.2(1/1 - 1/3) et 1/3x5 = 1.2(1/3 - 1/5) etc... Il ne reste alors que le premier et le dernier terme associé du signe négatif.

Cas général :

On répète exactement la même astuce. Si l'idée est la même, la mise en œuvre est un peu plus lourde. On suppose la formule démontrée à l'ordre n - 1, démontrons là à l'ordre n. La formule (1) et l'hypothèse de récurrence nous donne :

$b_{n,2i} =\sum_{j=0}^{n-2i}\frac 1{(2(n-j)-1)(2(n-j)-3)}\cdot \left( \frac 1{(2i-2)!}+ \sum_{k=1}^{i-1} \left( \frac {(-1)^k}{(2(i-k-1))!k!2^k}\prod_{l=1}^k\frac 1{2(n-j-l)-3} \right) \right)$

Pour guider l'intuition, on peut l'appliquer au couple (6,4) par exemple. On obtient :

$b_{6,4} = \frac 1{11\times 9}\left(\frac 12 - \frac 1{2 \times 7}\right) + \frac 1{9\times 7}\left(\frac 12 - \frac 1{2 \times 5}\right) + \frac 1{7\times 5}\left(\frac 12 - \frac 1{2 \times 3}\right)$

On remarque que la fraction ajoutée par la formule (1) s'intègre harmonieusement dans le produit de droite, ce qui simplifie l'expression et donne, dans l'exemple :

$b_{6,4} = \left(\frac 1{2\times 11\times 9} - \frac 1{2\times 11\times9\times 7}\right) + \left(\frac 1{2\times 9\times 7} - \frac 1{2\times 9\times 7\times 5}\right) + \left(\frac 1{2\times 7\times 5} - \frac 1{2\times 7\times 5\times 3}\right)$

Et dans le cas général :

$b_{n,2i}=\sum_{j=0}^{n-2i}\sum_{k=0}^{i-1} \left( \frac {(-1)^k}{(2(i-k-1))!k!2^k}\prod_{l=1}^{k+2}\frac 1{2(n-j-l)+1}\right)$

Ce que l'on peut plus agréablement écrire :

$b_{n,2i} = \sum_{k=0}^{i-1} \left( \frac {(-1)^k}{(2(i-k-1))!k!2^k}\sum_{j=0}^{n-2i}\prod_{l=1}^{k+2}\frac 1{2(n-j-l)+1}\right)$

Ce qui revient à considérer le coefficient du monôme comme la somme alternée de i suites. Dans l'exemple i est égal à 2 :

$b_{6,4} = \frac 12\left(\frac 1{11\times 9} + \frac 1{9\times 7} + \frac 1{7\times 5} \right) - \frac 12\left(\frac 1{11\times 9\times 7} + \frac 1{9\times 7\times 5} + \frac 1{7\times5\times 3}\right)$

Il est temps d'appliquer la même astuce qui a permis de débloquer la récurrence pour i égal à 1 :

$b_{n,2i} = \sum_{k=0}^{i-1} \left( \frac {(-1)^k}{(2(i-k-1))!k!2^k}\cdot \frac 1{2(k+1)}\sum_{j=0}^{n-2i} \left(\prod_{l=2}^{k+2}\frac 1{2(n-j-l)+1} - \prod_{l=1}^{k+1}\frac 1{2(n-j-l)+1}\right) \right)$

Ce qui revient à dire que :

$\frac 1{11\times 9} = \frac 12\left(\frac 19 - \frac1{11}\right) \quad\text{et}\quad \frac 1{11\times 9\times 7} = \frac 14\left(\frac 1{9\times 7} - \frac1{11\times 9}\right)$

Et, comme précédemment, tous les termes sous le signe somme s'annulent, sauf le premier et le dernier, ce qui permet une simplification :

$b_{n,2i} = \sum_{k=0}^{i-1} \left( \frac {(-1)^k}{(2(i-k-1))!(k+1)!2^{k+1}} \left(\prod_{l=2}^{k+2}\frac 1{2(2i-l)+1} - \prod_{l=1}^{k+1}\frac 1{2(n-l)+1}\right) \right)$

On peut maintenant recomposer la fraction en un terme constant et un autre dépendant de n. En incrémantant k d'une unité :

$b_{n,2i} = \sum_{k=1}^{i} \left(\frac {(-1)^{k+1}}{(2(i-k))!k!2^k} \prod_{l=2}^{k+1}\frac 1{2(2i-l)+1}\right) + \sum_{k=1}^{i} \left( \frac {(-1)^{k}}{(2(i-k))!k!2^k}\prod_{l=1}^{k}\frac 1{2(n-l)+1}\right)$

Dans l'exemple, la traduction de la formule donne bien l'expression recherchée :

$b_{6,4} = \left(\frac 14\cdot \frac 15 - \frac 18\cdot \frac 1{5\times3}\right) + \left(-\frac 14\cdot \frac 1{11} + \frac 18\cdot \frac 1{11\times 9}\right) = \frac 1{24} + \frac {-1}{2!1!2^1(11)} + \frac 1{1!2!2^2(11\times 9)}$

Calcul de la limite :

A droite, on trouve bien le terme recherché dans la formule de récurrence. On remarque d'ailleurs que si n grandit indéfiniment, il tend vers 0. À gauche, on dispose d'un terme indépendant de n qui est la limite recherchée et que l'on note l_i. Encore faut-il montrer que cette fraction correspond à une étrange manière d'écrire l'inverse de la factorielle de 2.i. Pour y voir plus clair, un exemple numérique est bienvenu. Cette fois ci, choisissons 3 pour valeur de i, il correspond au calcul de la limite du coefficient de degré 6 :

$l_3 = \frac 1{(4!)(2) (9)}- \frac 1{(2!)(2\times 4) (9\times 7)} + \frac 1{1(2\times 4\times 6) (9\times 7\times 5)}$

Une méthode un peu brutale consiste à réduire cette expression au même dénominateur. On remarque que, pour obtenir 6! le premier facteur du dénominateur nous permet de monter jusqu'à 4 ou encore 2.i - 2 dans le cas général, le deuxième contient le facteur 6 ou 2.i et le troisième le facteur 5 ou 2.i - 1 . Déplaçons les dans le premier facteur, pour plus de clarté :

$l_3 = \frac {(1)(4\times 6) (7\times 5) - (3\times 4)(6)(5) + (4!)(1)(1)}{(4!)(2\times 4\times 6) (9\times 7\times 5)} = \frac {(4!)(1)(1) - (3\times 4)(6)(5) + (1)(4\times 6)(7\times 5)}{(6!)(2\times 4) (9\times 7)}$

Ce qui, en termes généraux s'écrit :

$l_i = \frac {\sum_{k=1}^{i} N_{k,1}}{(2i)!\prod_{j=1}^i (2i +2j -1)(2i-2j)} \quad\text{avec}\quad N_{k,1} = (-1)^{k+1}\frac{(2i-2)!}{(2k-2)!}\prod_{j=1}^{k-1}(2i - 2j + 2)\prod_{j=1}^{k-1}(2i + 2j -3)$

Il s'agit maintenant de simplifier numérateur et dénominateur par les facteurs parasites, dans notre exemple on en trouve 4, à savoir 2, 4, 9 et 7 et dans le cas général il en existe 2.i - 2. Il est judicieux de commencer par le facteur 2.i + 1, on le trouve dans tous les termes du numérateur sauf les deux premiers. Dans l'exemple, cette valeur correspond à 7 :

$- (3\times 4)(6)(5) + (4!)(1)(1) = (3\times 4)(2 -6\times 5) = -(3\times 4)(7 \times 4)$

Ce qui permet de simplifier en haut et en bas par les facteurs 7 et 4 :

$l_3 = \frac {- (3\times 4)+ (1)(6)(5)}{(6!)\times 2 \times 9}$

Dans le cas général :

$N_{1,1} + N_{2,1} = \frac{(2i-2)!}{2!}\cdot\Big(2 - 2i(2i-1)\Big) = -\frac{(2i-2)!}{2!}(2i-2)(2i+1)$

La même simplification permet d'écrire :

$l_i = \frac {\sum_{k=2}^{i} N_{k,2}} {(2i)!\prod_{j=2}^i (2i +2j -1)(2i-2j)}\quad\text{et}\quad N_{2,2} =-\frac{(2i-2)!}{2!},\; \forall k \ge 2\quad (2i-2)(2i+1)\cdot N_{k,2} = N_{k,1}$

Dans l'exemple numérique, le même calcul permet de venir à bout des facteurs 2 et 9, ce qui permet d'atteindre notre objectif. Cette démarche est générique et permet la simplification par (2.i + 3) et (2.i - 4) :

$N_{2,2} + N_{3,2} = \frac{(2i-2)!}{4!}\cdot\Big(2i(2i-1)- 12\Big) = \frac{(2i-2)!}{4!}(2i-4)(2i+3)$

Au bout de k étapes de cette nature on trouve que l'expression de la constante est bien l'inverse de (2.i)!, ce qui termine le calcul des coefficients du polynôme k_n(t).

Convergence de la suite de polynômes k_p :

La convergence normale sur le disque fermé de rayon R, où R est un réel strictement positif, est maintenant simple à établir. Le raisonnement est analogue à celui sur la fonction exponentielle. Soit ε un réel strictement positif. La série de terme général R^2k/(2k)! est convergente, ce qui montre l'existence d'un entier N tel qu'une section finissante commençant par l'indice n choisi plus grand que N₁ soit majoré par ε/3. On en déduit que la section finissante équivalence de la fonction cosinus est aussi majorée par ε/3. Une section finissante équivalente pour le polynôme k_p l'est tout autant car ses coefficients sont, soit nuls, soit en valeur absolue majoré par ceux de la fonction cosinus.

Pour les n premiers termes initiaux, comme les coefficients des monômes constituant k_p tendent vers ceux de la série entière cosinus et que le nombre de termes est fini, il existe N tel que le module de la différence des deux sections commençantes de la fonction cosinus et de k_p, si p est choisi plus grand que N sera aussi plus petite de ε/3.

On en déduit que si p est plus grand que N et si t est, en module, majoré par R, la différence entre cos(t) est k_p(t) est, en module, majorée par ε, ce qui montre la convergence uniforme de la suite k_p(t) vers la fonction cosinus.

$|\cos(t) - k_p(t)| \le \left|\sum_{i=0}^n \left(\frac {{-1}^i}{(2i)!} - b_{p,2i}\right)t^{2i}\right| + \left|\sum_{i=n+1}^{\infty} \frac {{-1}^i}{(2i)!}t^{2i}\right| + \left|\sum_{i=n+1}^{\infty} b_{p,2i}t^{2i}\right|\le \epsilon$

Notes et références

↑ Johann Heinrich Lambert Mémoire sur quelques propriétés remarquables des quantités transcendantes circulaires et logarithmiques Mémoires de l'Académie des Sciences de Berlin, 17 1761 pp 265-322
↑ M. Serfati Fragments d'histoire des mathématiques. T. 4. Quadrature du cercle, fractions continues et autres contes APMEP Paris 1992
↑ ^{a et b} H. Padé Mémoire sur les développements en fractions continues de la fonction exponentielle Annales scientifiques de l'École Normale Supérieure Sér. 3 pp 395-426 (1899) Lire en Pdf
↑ C'est par exemple le cas chez Padé : Sur les fractions approchées d'une fonction par des fractions rationnelles Annales scientifique de l'E.N.S. 3^ième série tome 9 p 38 1892
↑ L. Euler Introductio in analysin infinitorum t I §§ 368-373 1748 (réédition Birkhäuser Basel 1980 (ISBN 3764314079))
↑ J. L. Lagrange Sur l'usage des fractions continues dans le calcul intégral Nouveaux mémoires de l'Académie royale des sciences et Belles lettres de Berlin 1776
↑ C. F. Gauss Disquisitiones generales circa seriem infinitam ... Commentationes societatis regiae scientiarum Gottingensis recentiores, 2 1813
↑ H. Padé Mémoire sur les développements en fractions continues de la fonction exponentielle Annales scientifiques de l'École Normale Supérieure Sér. 3 p 395 (1899) Lire en Pdf
↑ B. Riemann Sur le développement du quotient de deux séries hypergéométriques en fraction continue infinie 1863 Œuvre de Riemann p 424 2^ième édition 1873 Lire sur Gallica
↑ T. Rivoal Séries hypergéométriques et irrationalité des valeurs de la fonction zêta de Riemann Journal de théorie des nombres de Bordeaux tome 15 N° 1 2003 pp 351-365 (2003)
↑ Voir par exemple Henri Eugène Padé par le site historique de l'Université de St Andrew
↑ C. Hermite Sur la fonction exponentielle Compte rendu de l'Académie des sciences p 18 (1873) lire sur Gallica
↑ Lettre écrite à Carl Wilhelm Borchardt : C. Brezinski Histoires de sciences : Inventions, découvertes et savants l'Harmattan p 14 2006 (ISBN 2296003508)
↑ Voir par exemple H. Poincaré méthodes nouvelles de la mécanique céleste 3 vol Gauthier-Villars Paris 1892-1899
↑ H. Poincaré Notice sur Halphen Journal de l'Ecole Polytechnique 60^ième cahier pp 137-161 1890
↑ H. Padé Sur la représentation approchée d'une fonction par des fractions rationnelles Thèse de Doctorat présentée à l'Université de la Sorbonne 1892
↑ T. J. Stieltjes Recherches sur les fractions continues Annales de la faculté des sciences de Toulouse 1894 Lire sur Gallica
↑ Voir par exemple Eugène Henri Padé par le site historique de l'Université de St Andrew
↑ ce texte est extrait du mémoire qui remporta le prix : H. Padé Recherches sur la convergence des développements en fractions continues d'une certaine catégorie de fonction Annales scientifique que l'E.N.S 3^ième série tome 24 1907 p 341-400 Lire en Pdf
↑ Cette définition est par exemple choisie par Wolfram dans sa page sur les approximants de Padé par E. W. Weisstein
↑ Cette proposition, ainsi que la définition de réduite correspond au choix de Henri Padé dans son article Sur les fractions approchées d'une fonction par des fractions rationnelles Annales scientifique de l'E.N.S. 3^ième série tome 9 pp 3-93 1892
↑ Cet exemple est choisi par Henri Padé : Sur les fractions approchées d'une fonction par des fractions rationnelles Annales scientifique de l'E.N.S. 3^ième série tome 9 p 16 1892
↑ H. Padé Mémoire sur les développements en fractions continues de la fonction exponentielle Annales scientifiques de l'École Normale Supérieure Sér. 3 p403 (1899)
↑ Heine Handbuch der Kugelfunctionnen Tome I p. 266 1878
↑ H. Padé Sur les fractions approchées d'une fonction par des fractions rationnelles Annales scientifique de l'E.N.S. 3^ième série tome 9 p 39 1892
↑ Elle provient de l'article :H. Padé Sur les fractions approchées d'une fonction par des fractions rationnelles Annales scientifique de l'E.N.S. 3^ième série tome 9 p 50 1892
↑ On en trouve une version sur : M.Gouy G.Huvent A. Ladureau Approximants de Padé Irem de Lille

Voir aussi

Bibliographie

Jean-Étienne Rombaldi, Interpolation & approximation, analyse pour l'agrégation, Vuibert, 2005
(en) C. Brezinski & M. R. Zaglia, Extrapolation Methods: Theory and Practice, North-Holland 1991 (ISBN 0444888144)
(en) G. A. Baker & P. Graves-Morris, Padé Approximants Encyclopedia of Mathematics and its Applications N° 59 2^nd Ed 1996 (ISBN 0521450071)

Liens externes

(fr) D. Vekemans Approximants de Padé Laboratoire de mathématiques pures et appliquées Joseph Liouville
(fr) M.Gouy G.Huvent A. Ladureau Approximants de Padé Irem de Lille
(en) E. W. Weisstein Padé Approximant MathWorld Une resource Wolfram Web
(fr) H. Padé Sur les fractions approchées d'une fonction par des fractions rationnelles Annales scientifique de l'E.N.S. 3^e série tome 9 pp 3-93 1892

Portail de l'analyse

Catégories :

Analyse complexe
Fraction continue
Transformation de suite

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Approximant de Padé de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Approximant De Padé — Le concept de l article doit son nom à Henri Padé (1863 1953) un mathématicien français. En mathématiques, et plus précisément en analyse complexe, l approximant de Padé est une méthode d approximation d une fonction analytique par … Wikipédia en Français
Approximant de Pade — Approximant de Padé Le concept de l article doit son nom à Henri Padé (1863 1953) un mathématicien français. En mathématiques, et plus précisément en analyse complexe, l approximant de Padé est une méthode d approximation d une fonction… … Wikipédia en Français
Approximant de padé — Le concept de l article doit son nom à Henri Padé (1863 1953) un mathématicien français. En mathématiques, et plus précisément en analyse complexe, l approximant de Padé est une méthode d approximation d une fonction analytique par … Wikipédia en Français
Approximant de Padé de la fonction exponentielle — Les travaux présentés dans cet article sont l œuvre d Henri Padé, un mathématicien français. En mathématiques, un approximant de Padé de la fonction exponentielle est une fraction rationnelle h(x) / k(x), où h(x) désigne un polynôme de degré p et … Wikipédia en Français
Padé approximant — is the best approximation of a function by a rational function of given order. Developed by Henri Padé, a Padé approximant often gives better approximation of the function than truncating its Taylor series, and it may still work where the Taylor… … Wikipedia
Padé table — In complex analysis, a Padé table is an array, possibly of infinite extent, of the rational Padé approximants : R m , n to a given complex formal power series. Certain sequences of approximants lying within a Padé table can often be shown to… … Wikipedia
Henri Padé — Naissance 17 décembre 1863 Abbeville (France) Décès 9 juillet 1953 (à 89 ans) Aix e … Wikipédia en Français
Henri Pade — Henri Padé Henri Padé Henri Eugène Padé (17 décembre, 1863 9 juillet, 1953) était un mathématicien français, qui est surtout connu pour son développement des méthodes d approximation des fonctions par des fonctions rationnelles. Il fut un élève… … Wikipédia en Français
Henri Padé — Henri Eugène Padé (December 17, 1863 – July 9, 1953) was a French mathematician, who is now remembered mainly for his development of approximation techniques for functions using rational functions. See also * Padé approximant * Padé table… … Wikipedia
Fraction continue et approximation diophantienne — Le mathématicien indien Âryabhata fait usage d approximations diophantiennes construites à l aide de fractions continues dès le Ve siècle, pour extraire des racines carrées. En mathématiques, la réduite d une fraction continue … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Approximant de Padé

Sommaire

Préambule

Présentation du concept

Approche par la fraction continue

Fonction tangente

Fonction exponentielle

Fragments d'histoire

Origine

Formalisation

Définitions et premières propriétés

Définitions

Premières propriétés

Table de Padé

Fraction continue

Généralités

Fraction continue simple

Fraction continue régulière

Convergence

Structure du domaine

Illustration par l'exemple de la fonction tangente

Notes et références

Voir aussi

Bibliographie

Articles connexes

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Approximant de Padé

Sommaire

Préambule

Présentation du concept

Approche par la fraction continue

Fonction tangente

Fonction exponentielle

Fragments d'histoire

Origine

Formalisation

Définitions et premières propriétés

Définitions

Premières propriétés

Table de Padé

Fraction continue

Généralités

Fraction continue simple

Fraction continue régulière

Convergence

Structure du domaine

Illustration par l'exemple de la fonction tangente

Notes et références

Voir aussi

Bibliographie

Articles connexes

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link