Apollonius de perga

Pour les articles homonymes, voir Apollonius.

Apollonius de Perga
Naissance	-262 Perga, actuellement Aksu en Turquie (Royaume séleucide)
Décès	-190 Alexandrie (Égypte)
Champ(s)	Astronomie, mathématiques
Célèbre pour	Sections coniques

Apollonius de Perga ou Apollonios de Pergé (v. 262 – v. 190 av. J.-C.) était un géomètre grec et un astronome, célèbre pour ses écrits sur les sections coniques. Ce fut Apollonius qui donna à l'ellipse, à la parabole, et à l'hyperbole les noms que nous leur connaissons. Les hypothèses des orbites excentriques, pour expliquer le mouvement apparent des planètes et la variation de vitesse de la Lune, lui sont aussi attribuées.

Pappus donna des indications sur une série d'ouvrages d'Apollonius perdus qui permirent la déduction de leurs contenus par les géomètres de la Renaissance. Sa méthodologie innovante et sa terminologie, spécialement dans le domaine des coniques, a influencé plusieurs mathématiciens postérieurs dont François Viète, Kepler, Isaac Newton et René Descartes.

Les Coniques

Les Éléments des coniques, sous leur version originale en grec, consistent en un ensemble de huit ouvrages dus à Apollonius. Les quatre premiers livres nous sont parvenus en grec, avec les commentaires d'Eutocius. Les livres cinq à sept ne nous sont parvenus que dans une traduction en langue arabe due à Thābit ibn Qurra, et revue par Nasir ad-Din at-Tusi ; le huitième livre a disparu. L'ensemble de cet ouvrage, avec une reconstitution du huitième livre, a été publié (texte grec et traduction latine), par Edmund Halley en 1710. Celui-ci a, de plus, traduit de l'arabe en 1706 deux autres ouvrages d'Apollonius : De rationis sectione.

L'analyse des Anciens

Outre les Coniques, Pappus mentionne plusieurs autres traités d'Apollonius (les titres en latin sont dus à Commandino) :

1. Λόγου ἀποτομή, De Rationis Sectione (« Sur la section de rapport »)
2. Χωρίου ἀποτομή, De Spatii Sectione (« Sur la section d'aire »)
3. Διωρισμένη τομή, De Sectione Determinata (« Sur la Section déterminée »)
4. Ἐπαφαί, De Tactionibus (« Les Contacts »)
5. Νεύσεις, De Inclinationibus (« Les inclinaisons »^[1])
6. Τόποι ἐπίπεδοι, De Locis Planis (« Les lieux plans »)

Ces traités, dont chacun comprenait deux livres, étaient compilés à l'époque où vivait Pappus avec les Coniques et trois ouvrages d'Euclide (le Livre des données, les Porismes et les Lieux plans) sous le titre générique de « Trésor de l'Analyse ».

Le propos de l'Analyse des Anciens, tel que l'expose Pappus dans le livre VII de sa « Collection Mathématique », était de trouver une construction à la règle et au compas d'un lieu géométrique donné, ou du moins d'inventorier les cas où une telle construction était possible. Malheureusement, Pappus n'a transmis que des résumés des livres d'Apollonius, de sorte que l'étendue et la portée des méthodes de l'analyse a fait l'objet de multiples gloses du XVI^e au XVIII^e siècle. S'appuyant sur les indices donnés par Pappus et leurs spéculations personnelles, une pléiade de mathématiciens fameux se sont essayés à reconstruire les traités perdus d'Apollonius dans leur ordre original.

La Section de rapport

Les deux livres du traité De rationis sectione sont consacrés au problème suivant : étant données deux droites et un point sur chacune d'elle, mener depuis un troisième point une droite telle qu'elle découpe deux segments (entre chaque point donné et le point d'intersection) dont les longueurs soient dans un rapport donné.

La section d'aire

Les deux livres du traité De Spatii Sectione discutent la résolution d'un problème similaire au précédent : il s'agit cette fois de découper deux segments dont le produit soit égal à un produit donné ; dans la terminologie géométrique des Anciens, l'énoncé demande que les deux segments déterminent un rectangle de surface égale à un rectangle donné.

Une copie arabe de « La Section de rapport » fut retrouvée à la fin du XVII^e siècle par Edward Bernard à la Bodleian Library. Bien qu'il eût commencé la traduction de ce document, ce fut Halley qui la mena à terme, et qui la publia en 1706 avec sa reconstitution du De Spatii Sectione.

La Section Déterminée

Le traité traduit par Commandino sous le titre De Sectione Determinata traite pour ainsi dire de problèmes à une dimension d'espace : il s'agit ici de construire sur une droite des segments qui soient dans un rapport donné^[2]. Plus précisément, les problèmes abordés sont les suivants : étant donnés deux, trois ou quatre points sur une droite, trouver un point tel que les segments qu'il forme avec les autres points déterminent deux à deux des rectangles qui soient dans un rapport donné ; ainsi :

• si deux points A, B sont donnés, trouver M tel que 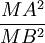soit égal à un rapport k donné ;
• si trois points A, B, C sont donnés, trouver M tel que 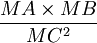soit égal à un rapport k donné. Une variante étudiée par Apollonius consiste à donner, outre A, B, C, un segment PQ et à chercher le(s) point(s) M tel que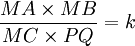
• si quatre points A, B, C, D sont donnés, trouver M tel que 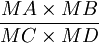soit égal à un rapport k donné.

Parmi les mathématiciens qui ont cherché à retrouver la solution d'Apollonius, citons :

• Snellius (Apollonius Batavus, Leyde, 1608);
• Alexander Anderson d'Aberdeen, dans son supplément à Apollonius Redivivus (Paris, 1612);
• et Robert Simson dans ses Opera quaedam reliqua (Glasgow, 1776), de loin la reconstitution la plus détaillée et la plus convaincante.

Les Contacts

Le traité De Tactionibus est consacré au problème générique suivant : trois éléments (points, droites ou cercles ; éventuellement un point, une droite et un cercle ; ou deux droites et un cercle, etc.) étant donnés de position, décrire un cercle passant par ces points, ou tangent à ces droites ou à ces cercles.

Le cas le plus difficile et le plus intéressant historiquement parlant est celui où les trois données sont trois cercles. François Viète, à la fin du XVI^e siècle, proposa ce problème (dit Problème d'Apollonius) à Adrien Romain, qui ne put le résoudre qu'en utilisant une hyperbole auxiliaire pour la construction. Viète lui répondit en publiant une solution « à la règle et au compas » (c'est-à-dire conforme aux exigences de l'analyse des Anciens), dans son livre Apollonius Gallus (Paris, 1600)^[3].

Les inclinaisons

Le propos du livre intitulé De Inclinationibus^[1] consiste à insérer un segment de longueur donnée entre deux droites sécantes (ou deux cercles, ou une droite et un cercle), de telle façon que ce segment, prolongé, passe par un point donné. Marin Ghetaldi et Hugo d'Omerique (Analyse géometrique, Cadix, 1698) se sont essayés à ce problème, mais la reconstitution la plus satisfaisante est sans doute celle de Samuel Horsley (1770).

Les lieux plans

De Locis Planis contient un ensemble de propositions relatives à des lieux qui s'avèrent être des droites ou des cercles. Comme Pappus ne donne que des cas particuliers de ce type de problème, les géomètres modernes ont longtemps été réduits aux conjectures pour trouver l'idée directrice de cette catégorie d'énoncés. Aussi chacun y est-il allé de son interprétation, à commencer par Pierre de Fermat^[4] (1636, publiée finalement dans ses Œuvres, tome I, 1891, pp. 3-51). Suivirent entre autres Frans van Schooten (Leyde, 1656) et Robert Simson (Glasgow, 1749).

Autres œuvres

Les Anciens mentionnent d'autre traités d'Apollonius qui ne sont pas parvenus jusqu'à nous :

1. Περί τοῦ πυρίου, Sur les miroirs ardents ; on pense que ce traité exploitait les propriétés focales des coniques.
2. Περί τοῦ κοχλίου, Sur l'hélice circulaire (citée par Proclus de Lycie)
3. Sur le rapport des volumes du dodécaèdre et de l'icosaèdre inscrits dans une sphère.
4. Ἡ καθόλου πραγματεία, traitait des principes généraux des mathématiques. Il comportait sans doute des remarques et des pistes d'amélioration pour les Éléments d'Euclide.
5. Dans un traité intitulé Ὠκυτόκιον ("Surgissement"), Apollonius démontrait, aux dires d'Eutocius, comment encadrer la valeur du nombre π (pi) plus précisément qu'Archimède ne l'avait fait : ce dernier avait en effet proposé 3-1/7 comme valeur par excès (3,142 857 142 857..., ) et 3-10/71 comme valeur par défaut (3,140 845 633 802 816 0...)
6. Le livre I de la « Collection mathématique » de Pappus (malheureusement mutilé) résume un ouvrage d'Apollonius proposant un système de numération et de multiplication adapté à l'écriture des très grands nombres (cf. Pappus) mieux adapté au langage quotidien que celui proposé par Archimède dans son traité L'arénaire ;
7. un développement de la théorie des grandeurs irrationnelles du livre X d'Euclide, allant des irrationnels binômes aux irrationnels multinômes, et des irrationnels ordonnés aux irrationnels non-ordonnés (cf. les commentaires de Pappus au livre X Éléments d'Euclide, transmis par l'arabe et publiés par Woepcke, 1856).

Voir aussi

• Théorème de Descartes

Notes et références

Sources

• (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Apollonius of Perga ».
• Michel Chasles - « Aperçu historique sur l'origine et le développement des méthodes en géométrie » (1837), impr. Hayez, Bruxelles
• Paul ver Eecke - « La Collection Mathématique de Pappus d'Alexandrie », introduction (1932, rééd. 1982) - Libr. A. Blanchard, Paris
• Abel Rey, L'apogée de la science technique grecque, vol. V : L'essor de la mathématique, Albin Michel, coll. « L'Évolution de l'Humanité / La science dans l'Antiquité », Paris, 1948, 20×14 cm, 324 p., partie II, chap. I (« Les Neuseis et la division de l'angle ») 
• Henk Bos - « Redefining geometrical exactness » (2001) éd. Springer, coll. Sources and studies in the Hist. of Math. and Phys. Sc. (ISBN 0-387-95090-7)

• Portail des mathématiques
• Portail de la géométrie
• Portail de l’astronomie
• Portail de la Grèce antique