Espace ultramétrique
- Espace ultramétrique
-
Distance ultramétrique
En topologie, une distance ultramétrique est une distance d sur un ensemble X vérifiant l'inégalité ultratriangulaire :
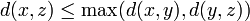 .
.
Des exemples importants interviennent en analyse p-adique.
Propriétés
- Dans un espace ultramétrique, la boule fermée de centre x et de rayon non nul r est un ouvert. La boule ouverte de centre x et de rayon non nul r est un fermé.
- Tout point d'une boule (ouverte ou fermée) en est son centre.
Exemples
 Portail de la géométrie
Portail de la géométrie
Catégorie : Distance remarquable
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Espace ultramétrique de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Ultramétrique — Distance ultramétrique En topologie, une distance ultramétrique est une distance d sur un ensemble X vérifiant l inégalité ultratriangulaire : . Des exemples importants interviennent en analyse p adique. Propriétés Dans un espace… … Wikipédia en Français
Espace De Cantor — On appelle espace de Cantor l espace produit . C est un espace compact métrisable à base dénombrable (en fait, pour un espace compact, être métrisable ou être à base dénombrable sont des propriétés équivalentes), totalement discontinu (on dit… … Wikipédia en Français
Espace de cantor — On appelle espace de Cantor l espace produit . C est un espace compact métrisable à base dénombrable (en fait, pour un espace compact, être métrisable ou être à base dénombrable sont des propriétés équivalentes), totalement discontinu (on dit… … Wikipédia en Français
Espace de Cantor — En mathématiques, plus précisément en topologie, on appelle espace de Cantor l espace produit . Propriétés C est un espace compact métrisable à base dénombrable (en fait, pour un espace compact, être métrisable ou être à base dénombrable sont des … Wikipédia en Français
Distance ultramétrique — En mathématiques, et plus précisément en topologie, une distance ultramétrique est une distance d sur un ensemble X vérifiant l inégalité ultratriangulaire : . Un espace métrique dont la distance vérifie cette propriété est dit ultramétrique … Wikipédia en Français
Norme ultrametrique — Norme ultramétrique En mathématiques, une norme ultramétrique, aussi appelée non archimédienne est une norme (sur un K espace vectoriel où le corps de base K est lui même muni d une valeur absolue ultramétrique) qui vérifie une condition plus… … Wikipédia en Français
Norme ultramétrique — En mathématiques, une norme ultramétrique, aussi appelée non archimédienne est une norme (sur un K espace vectoriel où K est un corps valué, i.e. muni d une valeur absolue elle même ultramétrique) qui vérifie une condition plus forte que l… … Wikipédia en Français
Distance Ultramétrique — En topologie, une distance ultramétrique est une distance d sur un ensemble X vérifiant l inégalité ultratriangulaire : . Des exemples importants interviennent en analyse p adique. Propriétés Dans un espace ultramétrique, la boule fermée de… … Wikipédia en Français
Distance ultrametrique — Distance ultramétrique En topologie, une distance ultramétrique est une distance d sur un ensemble X vérifiant l inégalité ultratriangulaire : . Des exemples importants interviennent en analyse p adique. Propriétés Dans un espace… … Wikipédia en Français
Distance (mathématiques) — Pour les articles homonymes, voir Distance. En mathématiques, une distance est une application qui formalise l idée intuitive de distance, c est à dire la longueur qui sépare deux points. C est par l analyse des principales propriétés de la… … Wikipédia en Français
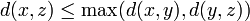 .
.