Espace discret

En topologie générale, un espace discret est un espace topologique D pour lequel toute partie de D est un ouvert. Autrement dit, la topologie 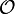de D (ensemble des ouverts de D) n'est autre que l'ensemble 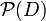des parties de D. Elle est appelée la topologie discrète.

La topologie discrète est la situation extrême opposée à la topologie grossière. Les espaces discrets apparaissent parfois comme premiers exemples dans les manuels d'introduction à la topologie. Au-delà de l'aspect illustratif, les espaces discrets apparaissent à des niveaux divers.

Sommaire 1 Définition 2 Propriétés 3 Distance discrète 4 Espace fini séparé 5 Fonctions sur les espaces discrets 6 Références 6.1 Manuels d'introduction

Définition

Un ensemble X peut admettre plusieurs topologies. Pour rappel, une topologie sur X est une famille de parties de X, stables par intersection finie et par réunion quelconque, contenant X et 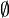. Un exemple a priori naïf de topologie est l'ensemble 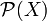de toutes les parties de X. Par définition, c'est la seule topologie pour laquelle toute partie de X en est un ouvert (autrement dit un élément de la topologie).

On dit que D=(X,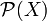) est un espace discret.

• Par définition, toutes les parties de D sont ouvertes ;
• Par passage au complémentaire, toutes les parties de D sont fermées.

Toute partie d'un ensemble X est la réunion des singletons qu'elle contient. Mathématiquement, on écrit, pour  :

.

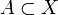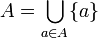Par conséquent, un espace topologique est discret ssi tous les singletons sont des ouverts. Et dans ce cas, la famille des singletons de X forment une base de la topologie de D.

Propriétés

Séparé

Tout espace discret D est séparé : on peut séparer deux points distincts x et y par deux ouverts disjoints U et V qui contiennent respectivement x et y. En effet, il suffit de prendre U  =  {x} et V  =  {y}, qui sont des ouverts de l'espace discret D !

Isolé

Mieux : tous les points d'un espace discret D sont isolés. Si x appartient à D, alors le singleton {x} est un ouvert de D.

Totalement disconnexe

Comme tous les singletons sont des ouverts, les seules parties connexes de D sont les singletons. On dit alors que D est totalement disconnexe.

Métrisable

La topologie d'un espace discret est métrisable. Autrement dit, il existe une distance d qui définit la topologie de D : voir le paragraphe suivant.

Distance discrète

La distance discrète sur un ensemble X est l'application 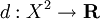, définie par :

d(x,y)	=	0 si x  =  y ;
		1 sinon.

Une boule de centre x et de rayon r est X si r est supérieur ou égal à 1 ; réduit au singleton {x} sinon. En particulier, les singletons de (X,d) sont des ouverts ; et par conséquent, (X,d) est un espace discret.

Espace fini séparé

Sur un ensemble fini X, la topologie discrète est l'unique topologie 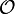pour laquelle (X,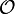) est un espace topologique séparé.

En effet, la topologie discrète sur X est une topologie séparée : on l'a vu. Réciproquement, fixons une topologie séparée 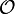sur l'ensemble fini X : pour tous points distincts x et y de X, il existe deux ouverts disjoints U_x et V_y qui contiennent respectivement x et y. Fixons x, notons U l'intersection des ouverts qui contiennent x. U est une intersection finie d'ouverts, donc un ouvert. Comme X est séparé, pour tout 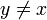il existe un ouvert qui contient x mais pas y. Donc l'intersection U ne peut pas contenir d'autre point que x. Par conséquent, U  =  {x} est un ouvert. On a démontré que tous les singletons sont des ouverts donc l'espace est discret.

Application

Dans un espace topologique séparé, une partie finie est, pour la topologie induite, un espace fini séparé. Par conséquent, toute partie finie d'un espace topologique séparé est un espace discret. Par contre, une partie dénombrable n'a aucune raison d'être une partie discrète. Par exemple, l'ensemble des nombres rationnels n'est pas une partie discrète de la droite réelle R pour sa topologie usuelle.

Fonctions sur les espaces discrets

Si D est un espace discret, et que Y est un espace topologique, alors toute application 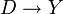est une application continue.

En effet, l'image réciproque d'un ouvert de Y est ... une partie quelconque de D, et donc un ouvert, puisque toute partie de D en est un ouvert. Par définition de la continuité en topologie générale, l'application est continue, comme annoncé.

Deux espaces topologiques homéomorphes ont même cardinalité, car tout homéomorphisme est d'abord une bijection. La réciproque est vérifiée pour les espaces discrets. Si D₁ et D₂ sont deux ensembles de même cardinalité, alors il existe une bijection 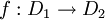. Mais, par ce qui précède, f et f ^{− 1} sont continues. Par conséquent, f est un homéomorphisme :

Deux espaces discrets sont homéomorphes ssi ils ont même cardinalité. Dans ce cas, toute bijection est un homéomorphisme.

Ces résultats peuvent se reformuler dans le langage des catégories.

Introduisons les deux catégories suivantes :

• La catégorie 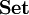des ensembles et des applications ;
• La catégorie 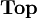des espaces topologiques et des applications continues.

Il existe un foncteur 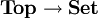, le foncteur d'oubli. Ce foncteur admet un adjoint, qui à un ensemble X, associe l'espace discret associé (X,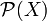). On est exactement en train de dire que, si X est un espace discret, alors pour tout espace topologique Y:

.

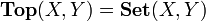Références

Manuels d'introduction

• Hervé Queffelec, Topologie - Cours et exercices corrigés, [détail des éditions]
• Nicolas Bourbaki, Eléments de mathématiques. Livre III : Topologie générale, [détail des éditions]
• Jean Dieudonné, Eléments d'analyse, t. I : Fondements de l'analyse moderne [détail des éditions]

• Portail des mathématiques