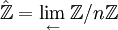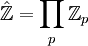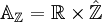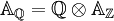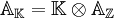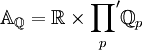Anneau adelique

Anneau adelique

Anneau adélique

En mathématiques et dans la théorie des nombres, l'anneau des adèles (ou anneau adélique) est un anneau topologique contenant le corps des nombres rationnels (ou, plus généralement, un corps de nombres algébriques), construit à l'aide de toutes les complétions du corps.

Le mot "adèle" est une abréviation pour "additive idele" ("idèle additif) (le fait que ce soit aussi un prénom féminin français est typique de l'esprit bourbakiste). Les adèles ont été appelés vecteurs de valuation ou répartitions avant 1950.

Sommaire

Définitions

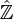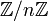La complétion profinie des entiers \hat{\mathbb{Z}} est la limite projective (ou limite inverse) des anneaux \mathbb{Z}/n\mathbb{Z} :

\hat{\mathbb{Z}} =\lim_{\leftarrow}\mathbb{Z}/n\mathbb{Z}

Par le théorème des restes chinois, elle est isomorphe au produit de tous les entiers p-adiques :

\hat{\mathbb{Z}} = \prod_{p} \mathbb{Z}_p

L'anneau adélique des entiers AZ est le produit

\mathbb{A}_\mathbb{Z} = \mathbb{R} \times \hat{\mathbb{Z}}

L'anneau adélique des rationnels AQ est le produit tensoriel

\mathbb{A}_\mathbb{Q} =\mathbb{Q}\otimes \mathbb{A}_\mathbb{Z}

(topologisé, c’est-à-dire que AZ en est un sous-anneau ouvert). Plus généralement, l'anneau adélique AK d'un corps de nombres algébriques quelconque K est le produit tensoriel

\mathbb{A}_\mathbb{K} =\mathbb{K}\otimes \mathbb{A}_\mathbb{Z}

(topologisé comme le produit de deg(K) copies de AQ).

L'anneau adélique des rationnels peut aussi être défini comme le produit restreint

\mathbb{A}_\mathbb{Q} = \mathbb{R} \times {\prod_{p}}' \mathbb{Q}_p

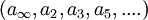de toutes les complétions p-adiques \mathbb{Q}_p et des nombres réels (ou en d'autres termes, comme le produit restreint de toutes les complétions des rationnels). Dans ce cas, le produit restreint signifie que pour un adèle (a_\infty, a_2, a_3, a_5, ....) tous les ap sont des entiers p-adiques, sauf un nombre fini d'entre eux.

L'anneau des adèles d'un corps de fonctions sur un corps fini peut être défini d'une manière similaire, comme le produit restreint de toutes les complétions de ce corps.

Propriétés

Les adèles rationnels A sont un groupe localement compact, les nombres rationnels \mathbb{Q} formant un sous-groupe discret co-compact. L'utilisation des anneaux adéliques en relation avec les transformations de Fourier a été exploitée dans la thèse de Tate. Une des propriétés-clef du groupe additif des adèles est qu'il est isomorphe à son dual de Pontryagin.

Applications

L'anneau des adèles est beaucoup utilisé en théorie des nombres, souvent comme anneau de coefficients dans des groupes matriciels : combiné avec la théorie des groupes algébriques, cela permet de construire les groupes algébriques adéliques. Le groupe des idèles de la théorie du corps de classes apparait comme le groupe 1 x 1 des matrices inversibles sur les adèles (ce n'est pas le sous-espace topologique correspondant, car l'inverse n'est pas continu pour cette topologie. À la place, les idèles sont identifiés avec le sous-ensemble fermé de toutes les paires (x,y) de A x A telles que xy=1, avec la topologie induite.)

Une étape importante dans le développement de la théorie a été la définition du nombre de Tamagawa pour un groupe algébrique adélique linéaire. C'est une mesure de volume reliant 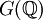G(\mathbb{Q}) avec G(A), disant comment 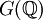G(\mathbb{Q}), qui est un groupe discret dans G(A), est plongé dans ce dernier. Une conjecture d'André Weil était que le nombre de Tamagawa était toujours 1 pour G groupe algébrique simplement connexe. Ceci découlait du traitement moderne de Weil des résultats de la théorie des formes quadratiques; la démonstration fut finalement complétée par Kottwitz.

Pendant ce temps, l'influence de l'idée du nombre de Tamagawa se faisait sentir dans la théorie des variétés abéliennes. Il semblait (et il semble toujours) qu'aucune adaptation directe n'en soit possible. Toutefois, durant la mise au point de la conjecture de Birch et Swinnerton-Dyer, la considération de ce que pour une courbe elliptique E, le groupe des points rationnels 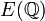E(\mathbb{Q}) pouvait être mis en relation avec 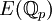E(\mathbb{Q}_p) fut une motivation et donna une direction de travail sur le chemin menant des résultats numériques à la formulation de la conjecture.

Voir aussi

  • Groupe algébrique adélique (ou groupe des idèles)
  • Fonction de Schwartz-Bruhat

Références

La plupart des livres sur la théorie algébrique des nombres moderne, tel que :

  • Algebraic Number Theory by J. W. S. Cassels, A. Frohlich ISBN 0-12-163251-2
Ce document provient de « Anneau ad%C3%A9lique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Anneau adelique de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Anneau Adélique — En mathématiques et dans la théorie des nombres, l anneau des adèles (ou anneau adélique) est un anneau topologique contenant le corps des nombres rationnels (ou, plus généralement, un corps de nombres algébriques), construit à l aide de toutes… …   Wikipédia en Français

  • Anneau adélique — En mathématiques et dans la théorie des nombres, l anneau adélique (ou anneau des adèles) est un anneau topologique contenant le corps des nombres rationnels (ou, plus généralement, un corps de nombres algébriques), construit à l aide de toutes… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Arithmetique modulaire — Arithmétique modulaire Couverture de l’édition originale des Recherches arithmétiques de Gauss, livre fondateur de l’arithmétique modulaire. En mathématiques et plus précisément en théorie algébrique des nombres, l’arithmétique modulaire est un… …   Wikipédia en Français

  • Arithmétique Modulaire — Couverture de l’édition originale des Recherches arithmétiques de Gauss, livre fondateur de l’arithmétique modulaire. En mathématiques et plus précisément en théorie algébrique des nombres, l’arithmétique modulaire est un ensemble de méthodes… …   Wikipédia en Français

  • Arithmétique modulaire (synthèse) — Arithmétique modulaire Couverture de l’édition originale des Recherches arithmétiques de Gauss, livre fondateur de l’arithmétique modulaire. En mathématiques et plus précisément en théorie algébrique des nombres, l’arithmétique modulaire est un… …   Wikipédia en Français

  • Arithmétique modulo — Arithmétique modulaire Couverture de l’édition originale des Recherches arithmétiques de Gauss, livre fondateur de l’arithmétique modulaire. En mathématiques et plus précisément en théorie algébrique des nombres, l’arithmétique modulaire est un… …   Wikipédia en Français

  • Arithmétique modulaire — Couverture de l’édition originale des Recherches arithmétiques de Gauss, livre fondateur de l’arithmétique modulaire. En mathématiques et plus précisément en théorie algébrique des nombres, l’arithmétique modulaire est un ensemble de méthodes… …   Wikipédia en Français

  • Liste Des Matières De La Théorie Des Nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 …   Wikipédia en Français

  • Liste des matieres de la theorie des nombres — Liste des matières de la théorie des nombres Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”