Similitude directe

Similitude directe

Similitude (géométrie)

Page d'aide sur l'homonymie Pour les articles homonymes, voir Similitude.
Les objets de même couleur sont semblables.

En géométrie, une similitude est une transformation qui, à toute figure, fait correspondre une figure semblable, c'est-à-dire de même forme.

Ainsi, par une similitude, tout carré a pour image un carré, tout triangle équilatéral un triangle équilatéral, tout cercle a pour image un cercle, etc.

Les similitudes conservent donc les barycentres et les cercles. Réciproquement, toute transformation bijective du plan qui conserve les cercles est une similitude (Cf. Théorème d'Abouabdillah)

Sommaire

Équivalence essentielle et définitions

Pour toute transformation f du plan euclidien, les propositions suivantes sont équivalentes.

  • f multiplie les distances par un réel strictement positif k ;
  • f conserve les rapports de distances ;
  • f conserve les angles géométriques (c'est-à-dire les mesures d'angles non orientés).

Une transformation du plan qui vérifie ces propositions est appelée une similitude du plan. Le nombre k est appelé le rapport de la similitude f.

Une similitude qui conserve les angles orientés est appelée similitude directe.

Exemples

Les similitudes de rapport 1 sont appelées isométries (notamment les rotations, translations, réflexions).

Les homothéties sont des similitudes. Il faut noter l'ambiguïté du mot rapport : le rapport d'une homothétie concerne des vecteurs, celui d'une similitude les distances. Ainsi, une homothétie de rapport k est une similitude de rapport |k|.

Étude par les points fixes

  • Une similitude plane qui admet trois points fixes non alignés est l'identité du plan.
  • Une similitude plane qui admet deux points fixes distincts A et B est soit l'identité du plan, soit la symétrie axiale d'axe (AB).
  • Une similitude directe qui admet deux points fixes distincts est donc l'identité.

On peut donc classer les similitudes directes suivant le nombre de leurs points fixes :

  • l'identité, pour laquelle tous les points du plan sont fixes ;
  • les similitudes directes sans point fixe ;
  • les similitudes directes avec un unique point fixe, qu'on appelle alors le centre de la similitude.

Similitudes planes directes

Mises à part les translations, toute similitude plane directe peut être décomposée en une homothétie et en une rotation de même centre.

Une isométrie qui conserve les angles orientés est appelée déplacement.

Forme complexe

Les calculs sont adaptés au plan complexe. La traduction d'une similitude directe s'y exprime par z' = az + b, où a et b sont des complexes, a non nul. Le rapport de la similitude est alors | a | , son angle arg(a).

Cas spéciaux :

  • Dans le cas où a = 1, la similitude est une translation.
  • Dans le cas où a = − 1, la similitude est une symétrie centrale de centre 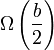\Omega \left(\frac b 2\right). On peut aussi la considérer comme une rotation de centre 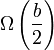\Omega \left(\frac b 2\right) et d'angle π, ou encore une homothétie de centre \Omega (\frac{b}{2}) et de rapport k = − 1.
  • Dans le cas où 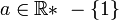a \in \mathbb{R*}\ -\left \{ 1 \right \} , alors la similitude est une homothétie de centre 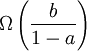\Omega \left(\frac{b}{1-a}\right) et de rapport a.

Définition par deux points et leurs images

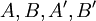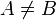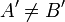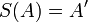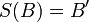
Soient A, B, A^\prime, B^\prime quatre points du plan tels que : A \neq B et A' \neq B'. Il existe une unique similitude directe S tel que S(A)=A^\prime et S(B)=B^\prime

Similitudes planes indirectes

Toute similitude non directe est la composée d'une similitude directe et d'une réflexion.

Forme complexe

La traduction d'une similitude indirecte s'exprime par 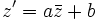z' = a \bar{z} + b, où a et b sont complexes, a non nul.

Le groupe des similitudes

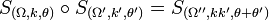
La composée de deux similitudes f et g est une similitude, dont le rapport est le produit des rapports de f et g. Dans le cas de deux similitudes directes, on a : S_{(\Omega,k,\theta)} \circ S_{(\Omega',k',\theta ')} = S_{(\Omega'',kk',\theta+\theta ')}

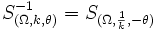La transformation réciproque d'une similitude f est une similitude, de rapport : l'inverse du rapport de f. Pour une similitude directe, on a : S^{-1}_{(\Omega,k,\theta)} = S_{(\Omega,\frac{1}{k},- \theta)}.

L'ensemble des similitudes du plan, muni de la loi de composition est donc un groupe, dont deux sous-groupes sont : le groupe des similitudes directes et le groupe des isométries (dont un sous-groupe est le groupe des déplacements).

  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Similitude (g%C3%A9om%C3%A9trie) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Similitude directe de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Similitude (géométrie) — Pour les articles homonymes, voir Similitude. Pour la similitude des triangles, voir Triangles semblables. En géométrie euclidienne, une similitude est une transformation qui multiplie toutes les distances par une constante fixe, appelée son… …   Wikipédia en Français

  • Invariant de similitude — Invariants de similitude En algèbre linéaire, un système complet d invariants pour la relation de similitude entre les matrices carrées de même taille à coefficients dans un corps est connu : ces invariants sont classiquement appelés… …   Wikipédia en Français

  • Invariants De Similitude — En algèbre linéaire, un système complet d invariants pour la relation de similitude entre les matrices carrées de même taille à coefficients dans un corps est connu : ces invariants sont classiquement appelés invariants de similitude. Ils… …   Wikipédia en Français

  • Invariants de similitude — En algèbre linéaire, un invariant de similitude est une quantité qu on peut associer à toute matrice carrée (à coefficients dans un corps commutatif fixé K), telle que pour deux matrices semblables cette quantité soit toujours la même. Exemples d …   Wikipédia en Français

  • Somme directe — Pour les articles homonymes, voir Somme. En mathématiques, et plus précisément en algèbre, le terme de somme directe désigne des ensembles munis de certaines structures, souvent construits à partir du produit cartésien d autres ensembles du même… …   Wikipédia en Français

  • FONCTIONS ANALYTIQUES - Représentation conforme — La représentation conforme la plus anciennement connue est la projection stéréographique, inventée par les Grecs (Hipparque, Ptolémée). Les problèmes cartographiques conduisirent à la découverte d’autres applications conservant les angles d’un… …   Encyclopédie Universelle

  • Application conforme — Transformation conforme Une transformation conforme est une transformation qui conserve les angles. Une France conforme, et... anticonforme Sommaire 1 Cas du plan 1.1 Exemples holomorphes …   Wikipédia en Français

  • Transformation conforme — En mathématiques, et plus précisément en géométrie et en analyse complexe, une transformation conforme est une transformation qui conserve les angles. Une France conforme, et... anticonforme Sommaire 1 Cas du plan …   Wikipédia en Français

  • Arithmétique complexe — Nombre complexe Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels.… …   Wikipédia en Français

  • Nombre Complexe — Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels. Les nombres… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”