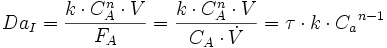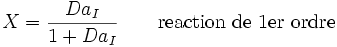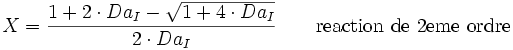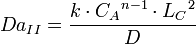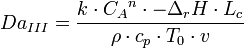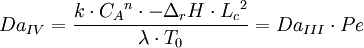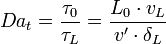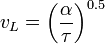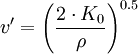Nombre de Damkohler

Nombre de Damkohler

Nombre de Damköhler

Le nombre de Damköhler (Da) est un nombre sans dimension utilisé en cinétique chimique pour définir les conditions opérationnelles d'une réaction. Il existe plusieurs variantes de ce nombre en fonction du système étudié[1].

Ce nombre porte le nom de Gerhard Damköhler, un chimiste allemand.

Sommaire

DaI

Le nombre de Damköhler DaI représente le rapport entre la vitesse de réaction consommant le réactif A et le flux du réactif A.

On le définit de la manière suivante

Da_I = \frac{k \cdot C_{A}^n \cdot V}{F_{A}} = \frac{k \cdot C_{A}^n \cdot V}{C_{A} \cdot \dot{V}} = \tau \cdot k \cdot {C_{a}}^{n-1}

avec:

  • k - constante de réaction
  • CA - concentration du réactif A
  • V - volume
  • n - ordre de la réaction
  • FA - flux du réactif A
  • τ - temps de passage

Ce nombre est très utile pour estimer la conversion des réacteurs continus. Les équations cinétiques peuvent être écrites pour obtenir l'équation suivante:

X = \frac{Da_I}{1+Da_I} \qquad \text{reaction de 1er ordre}


X = \frac{1+2 \cdot Da_I - \sqrt{1+4 \cdot Da_I}}{2 \cdot Da_I} \qquad \text{reaction de 2eme ordre}



Pour une bonne conversion, le nombre de Damköhler doit être grand. Comme valeur indicative, lorsque DaI < 0.1, alors X < 0.1 et si DaI > 10, alors X > 0.9[2]. Dans le cas d'un réacteur discontinu, le temps de passage est remplacé par le temps de réaction.


DaII

Le nombre de Damköhler DaII est utilisé en catalyse hétérogène. La réaction a lieu sur le catalyseur, en général un solide, et les réactifs doivent passer du solvant à la surface du catalyseur. Ce transfert de masse est limité par la diffusion du réactif au travers de la couche limite de diffusion qui se trouve à la surface du catalyseur. Le nombre de Damköhler devient dès lors le rapport entre la vitesse de la réaction et le flux des réactifs au travers de la couche de diffusion.

On le définit de la manière suivante

Da_{II} = \frac{k \cdot {C_{A}}^{n-1}\cdot {L_{C}}^2}{D}

avec:

  • k - Constante de réaction
  • CA - Concentration du réactif A
  • n - Ordre de la réaction
  • Lc - Longueur caractéristique
  • D - Coefficient de diffusion


DaIII

Le nombre de Damköhler DaIII est semblable au nombre de Damköhler DaI, mais il s'applique au transfert de chaleur. Il s'agit du rapport du flux de chaleur dégagé par la réaction sur le flux de chaleur évacué via un écoulement convectif.

On le définit de la manière suivante

Da_{III} = \frac{k \cdot {C_{A}}^n \cdot -\Delta_r H \cdot L_c}{\rho \cdot c_p \cdot T_0 \cdot v}

avec:

  • k - constante de réaction
  • CA - concentration du réactif A
  • n - ordre de la réaction
  • Lc - longueur caractéristique
  • -ΔrH - enthalpie de réaction
  • ρ - masse volumique
  • cp - capacité calorifique
  • T0 - température
  • v - vitesse du fluide


DaIV

Le nombre de Damköhler DaIV est le pendant du nombre de Damköhler DaII en transfert thermique. Il s'agit du rapport du flux de chaleur dégagé par la réaction sur le flux de chaleur évacué par conduction.

On le définit de la manière suivante

Da_{IV} = \frac{k \cdot {C_{A}}^n \cdot -\Delta_r H \cdot {L_c}^2}{\lambda \cdot T_0} = Da_{III} \cdot Pe

avec:

  • k - constante de réaction
  • CA - concentration du réactif A
  • n - ordre de la réaction
  • Lc - longueur caractéristique
  • -ΔrH - enthalpie de réaction
  • λ - conductivité
  • T0 - température
  • Pe - nombre de Péclet


Dat

Il existe encore un nombre de Damköhler turbulent Dat utilisé pour caractériser la turbulence et la forme des flammes dans les phénomènes de combustion.

On le définit de la manière suivante

Da_t = \frac{\tau_0}{\tau_L} = \frac{L_0 \cdot v_L}{v' \cdot \delta_L}

avec:

  • τ0 - temps de fluctuation
  • τL - temps chimique
  • δL - épaisseur de la flamme en régime laminaire
  • vL - vitesse de propagation du front de flamme
  • L0 - longueur caractéristique des tourbillons
  • v' - vitesse de fluctuation


La vitesse de propagation du front de flamme est définie de la manière suivante[3]

v_L = \left( \frac{\alpha}{\tau} \right)^{0.5}

avec

  • α - diffusivité thermique
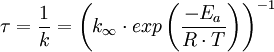
  • τ - temps de réaction \tau = \frac {1}{k} = \left( k_{\mathcal{1}} \cdot exp \left(\frac {-E_a}{R \cdot T} \right) \right)^{-1}


La vitesse de fluctuation est définie par

v' = \left( \frac{2 \cdot K_0}{\rho} \right)^{0.5}

avec

  • ρ - masse volumique
  • K0 - énergie cinétique turbulente


Quand Dat <1, le temps pour une modification de la composition chimique du front de flamme est plus grand que le temps pour un changement du mouvement du fluide. Ceci se traduit par une zone intermédiaire entre la flamme et la zone extérieure où les produits et les réactifs de la combustion se mélangent si bien que le front de la flamme n'est plus distinguable[4].

Notes et références

  1. ↑ (en) Carl W. Hall, Laws and Models:Science, Engineering and Technology, CRC Press, Boca Raton, 2000, 524 p. (ISBN 8449320186) 
  2. ↑ (en) H. Scott Fogler, Elements of Chemical Reaction Engineering, Pearson Educational International, 2006 (ISBN 0-130127839-8) 
  3. ↑ J. Warnatz, U. Maas, R.W. Dibble, Combustion: Physical and Chemical Fundamentals, Modeling and Simulation, Experiments, Pollutant Formation, Springer Berlin Heidelberg, 2006, 378 p. (ISBN 9783540259923), « 8 », p. 120 
  4. ↑ J. Warnatz, U. Maas, R.W. Dibble, Combustion: Physical and Chemical Fundamentals, Modeling and Simulation, Experiments, Pollutant Formation, Springer Berlin Heidelberg, 2006, 378 p. (ISBN 9783540259923), « 15 », p. 229 
  • Portail de la chimie Portail de la chimie
Ce document provient de « Nombre de Damk%C3%B6hler ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre de Damkohler de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Nombre de Damköhler — Le nombre de Damköhler (Da) est un nombre sans dimension utilisé en cinétique chimique pour définir les conditions opérationnelles d une réaction. Il existe plusieurs variantes de ce nombre en fonction du système étudié[1]. Ce nombre porte le nom …   Wikipédia en Français

  • Nombre adimensionnel — Grandeur sans dimension En physique, une grandeur sans dimension est une quantité permettant de décrire une caractéristique physique sans dimension ni unité explicite d expression. Elle est constituée du produit ou rapport de grandeurs à… …   Wikipédia en Français

  • Nombre adimentionnel — Grandeur sans dimension En physique, une grandeur sans dimension est une quantité permettant de décrire une caractéristique physique sans dimension ni unité explicite d expression. Elle est constituée du produit ou rapport de grandeurs à… …   Wikipédia en Français

  • Nombre sans dimension — Grandeur sans dimension En physique, une grandeur sans dimension est une quantité permettant de décrire une caractéristique physique sans dimension ni unité explicite d expression. Elle est constituée du produit ou rapport de grandeurs à… …   Wikipédia en Français

  • Nombre de Thiele — Le nombre de Thiele est un nombre sans dimension utilisé en cinétique chimique pour caractériser le facteur limitant pour une réaction catalytique hétérogène avec un catalyseur poreux. Il donne le rapport entre la vitesse de réaction sur le… …   Wikipédia en Français

  • Module de Thiele — Nombre de Thiele Le nombre de Thiele est un nombre sans dimension utilisé en cinétique chimique pour caractériser le facteur limitant pour une réaction catalytique hétérogène avec un catalyseur poreux. Il donne le rapport entre la vitesse de… …   Wikipédia en Français

  • Grandeur Sans Dimension — En physique, une grandeur sans dimension est une quantité permettant de décrire une caractéristique physique sans dimension ni unité explicite d expression. Elle est constituée du produit ou rapport de grandeurs à dimensions, de telle façon que… …   Wikipédia en Français

  • Grandeur sans dimension — En physique, une grandeur sans dimension (ou grandeur adimensionnelle) est une quantité permettant de décrire une caractéristique physique sans dimension ni unité explicite d expression. Elle est constituée du produit ou rapport de grandeurs à… …   Wikipédia en Français

  • Loi de similitude — Grandeur sans dimension En physique, une grandeur sans dimension est une quantité permettant de décrire une caractéristique physique sans dimension ni unité explicite d expression. Elle est constituée du produit ou rapport de grandeurs à… …   Wikipédia en Français

  • Nombres sans dimension — Grandeur sans dimension En physique, une grandeur sans dimension est une quantité permettant de décrire une caractéristique physique sans dimension ni unité explicite d expression. Elle est constituée du produit ou rapport de grandeurs à… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”