Huitième problème de Hilbert

Huitième problème de Hilbert

Hypothèse de Riemann

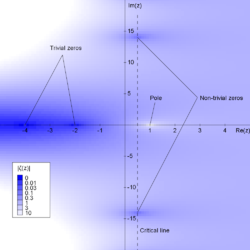Représentation de la valeur absolue de la fonction zêta de Riemann.

L'hypothèse de Riemann est une conjecture formulée en 1859 par le mathématicien Bernhard Riemann. Elle dit que les zéros non triviaux de la fonction zêta de Riemann ont tous pour partie réelle 1/2. Sa démonstration améliorerait la connaissance de la répartition des nombres premiers.

Cette conjecture constitue l'un des problèmes non résolus les plus importants des mathématiques du début du XXIe siècle : elle est l'un des fameux problèmes de Hilbert proposés en 1900, et fait l'objet d'un des problèmes Clay pour le troisième millénaire, doté d'un prix d'un million de dollars américains.

Sommaire

Historique

Riemann mentionna la conjecture, appelée plus tard « hypothèse de Riemann », dans son article paru en 1859 Sur le nombre de nombres premiers inférieurs à une taille donnée (Über die Anzahl der Primzahlen unter einer gegebenen Grösse en allemand)[1], mais cette conjecture n'étant pas le sujet principal de son article, il n'attend pas de démonstration. 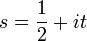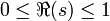Riemann savait que les zéros non triviaux de la fonction zêta étaient distribués symétriquement autour de la ligne s = \frac{1}{2} + it\, et savait que tous les zéros non triviaux se trouvaient dans la bande 0 \le \Re(s) \le 1.

En 1896, Hadamard et de la Vallée-Poussin prouvèrent indépendamment qu'aucun zéro ne pouvait se trouver sur la ligne 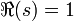\Re(s) = 1\,, ainsi que tous les zéros non triviaux devaient se trouver dans l'intérieur de la bande critique 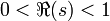0 < \Re(s) < 1\,. Ceci était un résultat-clé dans la première démonstration complète du théorème des nombres premiers.

En 1900, Hilbert inclut l'hypothèse de Riemann dans sa célèbre liste de 23 problèmes non résolus — il fait partie du 8e problème, celle-ci comprenant aussi la conjecture de Goldbach. Il aurait dit à propos de ce problème : « Si je devais me réveiller après avoir dormi pendant mille ans, ma première question serait : L'hypothèse de Riemann a-t-elle été prouvée ? »[2]. L'hypothèse de Riemann est le seul problème de Hilbert à figurer dans la liste des problèmes du prix du millénaire de l'institut de mathématiques Clay.

En 1914, Hardy prouva qu'il y a une infinité de zéros sur la droite critique 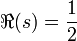\Re(s) = \frac{1}{2}\,. Cependant il reste possible qu'il y ait une infinité de zéros non triviaux ailleurs. Des travaux ultérieurs de Hardy et Littlewood en 1921 et de Selberg en 1942 ont donné une estimation de la densité moyenne de zéros sur la droite critique.

Des travaux récents se sont focalisés sur le calcul explicite d'endroits où se trouvent beaucoup de zéros (dans l'espoir de trouver un contre-exemple) et de placer des bornes supérieures sur la proportion de zéros se trouvant ailleurs que sur la droite critique (dans l'espoir de la réduire à zéro).

Tests numériques

En l'absence de démonstration validée par la communauté des mathématiciens, Andrew M. Odlyzko s'est spécialisé dans le calcul numérique des zéros non triviaux de la fonction. On affirme ainsi généralement que le milliard et demi de zéros calculés vérifient tous l'hypothèse de Riemann ; ce qui signifie qu'ils sont positionnés assez près de la droite critique (au sens que l'imprécision de calcul est telle qu'ils peuvent y être exactement).

Essais de démonstration

De nombreuses preuves supposées de l'hypothèse de Riemann sont régulièrement proposées, principalement sur Internet, ainsi que quelques infirmations, souvent le fait de mathématiciens en marge du système universitaire traditionnel. Aucun de ces travaux n'a pour le moment reçu l'assentiment de la communauté mathématique.

Le site [1] recense quelques-unes de ces supposées preuves (y compris des « preuves » que l'hypothèse serait fausse), et aussi quelques parodies.

Voir aussi

Références

  1. ↑ Le manuscrit original
  2. ↑ R.Bellman, A Brief Introduction of Theta Functions (Holt, 1961) p. 33-34

Sources

  • (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Riemann hypothesis ».

Bibliographie

  • Karl Sabbagh, The Riemann Hypothesis: The Greatest Unsolved Problem in Mathematics, Farrar, Straus and Giroux, 2004. ISBN 0-374-52935-3.
  • Page d'Andrew M. Odlyzko, mathématicien spécialisé dans le calcul numérique des zéros non triviaux de la fonction zéta.
  • Marcus du Sautoy, La Symphonie des nombres premiers, Editions Héloïse d'Ormesson, ISBN 2-35087-011-1

Articles connexes

Liens externes


Problèmes de Hilbert
Premier problème - Deuxième problème - Troisième problème - Quatrième problème - Cinquième problème - Sixième problème - Septième problème - Huitième problème - Neuvième problème - Dixième problème - Onzième problème - Douzième problème - Treizième problème - Quatorzième problème - Quinzième problème - Seizième problème - Dix-septième problème - Dix-huitième problème - Dix-neuvième problème - Vingtième problème - Vingt-et-unième problème - Vingt-deuxième problème - Vingt-troisième problème


Problèmes du prix du millénaire
Hypothèse de Riemann - Conjecture de Poincaré - P=NP - Conjecture de Hodge - Conjecture de Birch et Swinnerton-Dyer - Équations de Navier-Stokes - Équations de Yang-Mills


  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Hypoth%C3%A8se de Riemann ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Huitième problème de Hilbert de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Seizième problème de Hilbert — Le seizième problème de Hilbert est l un des 23 problèmes de Hilbert. Il comporte deux parties. La première concerne le nombre de branches réelles (ovales) d une courbe algébrique, et leur disposition ; de nombreux résultats modernes… …   Wikipédia en Français

  • Dixième problème de Hilbert — Le dixième problème de Hilbert demande de trouver une méthode algorithmique générale pour la recherche des solutions entières des équations diophantiennes à plusieurs inconnues, c est à dire des équations polynômiales à coefficients entiers. Il… …   Wikipédia en Français

  • Troisieme probleme de Hilbert — Troisième problème de Hilbert Le troisième problème de Hilbert est l un des 23 problèmes de Hilbert. Considéré comme le plus facile, il traite de la géométrie des polyèdres. Étant donnés deux polyèdres d égal volume, est il possible de découper… …   Wikipédia en Français

  • Troisième problème de Hilbert — Le troisième problème de Hilbert est l un des 23 problèmes de Hilbert. Considéré comme le plus facile, il traite de la géométrie des polyèdres. Étant donnés deux polyèdres d égal volume, est il possible de découper le premier polyèdre en des… …   Wikipédia en Français

  • Troisième problème de hilbert — Le troisième problème de Hilbert est l un des 23 problèmes de Hilbert. Considéré comme le plus facile, il traite de la géométrie des polyèdres. Étant donnés deux polyèdres d égal volume, est il possible de découper le premier polyèdre en des… …   Wikipédia en Français

  • Neuvieme probleme de Hilbert — Neuvième problème de Hilbert Le neuvième problème de Hilbert est l un des vingt trois problèmes ouverts proposés comme défis du XXe siècle par David Hilbert au second congrès international de mathématiques en 1900. Il consiste à généraliser… …   Wikipédia en Français

  • Neuvième Problème De Hilbert — Le neuvième problème de Hilbert est l un des vingt trois problèmes ouverts proposés comme défis du XXe siècle par David Hilbert au second congrès international de mathématiques en 1900. Il consiste à généraliser la loi de réciprocité… …   Wikipédia en Français

  • Neuvième problème de hilbert — Le neuvième problème de Hilbert est l un des vingt trois problèmes ouverts proposés comme défis du XXe siècle par David Hilbert au second congrès international de mathématiques en 1900. Il consiste à généraliser la loi de réciprocité… …   Wikipédia en Français

  • Septieme probleme de Hilbert — Septième problème de Hilbert Le septième problème de Hilbert concerne l irrationalité et la transcendance de certains nombres (Irrationalität und Transzendenz bestimmter Zahlen). Dans sa formulation géométrique, il demande quand l assertion… …   Wikipédia en Français

  • Septième problème de hilbert — Le septième problème de Hilbert concerne l irrationalité et la transcendance de certains nombres (Irrationalität und Transzendenz bestimmter Zahlen). Dans sa formulation géométrique, il demande quand l assertion suivante est démontrable :… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”