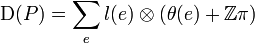Troisième problème de hilbert

Troisième problème de Hilbert

Le troisième problème de Hilbert est l'un des 23 problèmes de Hilbert. Considéré comme le plus facile, il traite de la géométrie des polyèdres.

Étant donnés deux polyèdres d'égal volume, est-il possible de découper le premier polyèdre en des polyèdres et de les rassembler pour former le second polyèdre ?

Hilbert conjectura que ce n'était pas toujours vrai. Ce fut confirmé dans l'année par son élève, Max Dehn, qui fournit un contre-exemple.

Pour le problème analogue concernant les polygones, la réponse est affirmative. Le résultat est connu sous le nom du théorème de Wallace-Bolyai-Gerwein.

Réponse de Dehn

Dehn utilise l'algèbre pour nier la possibilité du découpage. Lorsque le premier polyèdre peut être effectivement découpé en des polyèdres qui se rassemblent pour former le second, les polyèdres sont dits congruents.

À chaque polyèdre P, on associe une valeur, appelée « invariant de Dehn » D(P) telle que :

D est additive : si P se découpe par section par un unique plan en deux polyèdres P₁ P₂, D(P)=D(P₁)+D(P₂).

En particulier, si deux polyèdres P et Q sont congruents, alors ils ont le même invariant de Dehn.

Le cube a un invariant de Dehn nul, alors que le tétraèdre a un invariant de Dehn positif. Ces deux polyèdres ne sont pas congruents.

L'invariant se définit sur les longueurs et les angles dièdres. Observons :

Un découpage par un plan divise les longueurs de certains côtés en deux. Il faut donc que l'invariant soit additif en ces longueurs.
De même, si un polyèdre est divisé selon un côté, l'angle dièdre correspondant est coupé en deux. Il faut donc que l'invariant soit additif en ces angles.
Enfin, le découpage fait apparaître de nouveaux côtés ; donc des nouvelles longueurs, et des nouveaux angles dièdres. Ces contributions doivent s'annuler.

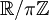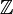L'invariant de Dehn se définit comme un élément du produit tensoriel du corps des nombres réels $\mathbb R$ par le quotient $\mathbb R/\pi\mathbb Z$ . Le produit tensoriel est pris sur $\mathbb Z$ .

$\operatorname{D}(P) = \sum_{e} l(e)\otimes (\theta(e)+\mathbb{Z}\pi)$

où l(e) est la longueur du côté e, θ(e) est l'angle dièdre entre les faces adjacentes à e, et la somme est prise sur tous les cotés du polyèdre.

Au-delà du problème de Hilbert

Sylder démontra en 1965 que deux polyèdres sont congruents si et seulement si ils ont même volume et même invariant de Dehn.

En 1990, Dupon en donne une preuve simplifiée en réinterprétant comme un théorème sur l'homologie de certains groupes classiques.

Motivations

La formule du volume d'une pyramide était connue d'Euclide (proposition 7 du livre XII des Eléments) : 1/3 × aire de la base×hauteur. Mais contrairement à l'aire des triangles ou des parallélogrammes qui peuvent se comparer par simple découpage avec celle d'un rectangle, la démonstration du volume de la pyramide fait appel à la complexe méthode d'exhaustion, ancêtre du calcul intégral. Gauss le déplora dans l'une de ses lettres adressées à Gerling.

Problèmes de Hilbert
Premier problème - Deuxième problème - Troisième problème - Quatrième problème - Cinquième problème - Sixième problème - Septième problème - Huitième problème - Neuvième problème - Dixième problème - Onzième problème - Douzième problème - Treizième problème - Quatorzième problème - Quinzième problème - Seizième problème - Dix-septième problème - Dix-huitième problème - Dix-neuvième problème - Vingtième problème - Vingt-et-unième problème - Vingt-deuxième problème - Vingt-troisième problème

Portail des mathématiques

Ce document provient de « Troisi%C3%A8me probl%C3%A8me de Hilbert ».

Catégorie : Problème de Hilbert

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Troisième problème de hilbert de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Troisieme probleme de Hilbert — Troisième problème de Hilbert Le troisième problème de Hilbert est l un des 23 problèmes de Hilbert. Considéré comme le plus facile, il traite de la géométrie des polyèdres. Étant donnés deux polyèdres d égal volume, est il possible de découper… … Wikipédia en Français
Troisième problème de Hilbert — Le troisième problème de Hilbert est l un des 23 problèmes de Hilbert. Considéré comme le plus facile, il traite de la géométrie des polyèdres. Étant donnés deux polyèdres d égal volume, est il possible de découper le premier polyèdre en des… … Wikipédia en Français
Dixième problème de Hilbert — Le dixième problème de Hilbert demande de trouver une méthode algorithmique générale pour la recherche des solutions entières des équations diophantiennes à plusieurs inconnues, c est à dire des équations polynômiales à coefficients entiers. Il… … Wikipédia en Français
Huitième problème de Hilbert — Hypothèse de Riemann Représentation de la valeur absolue de la fonction zêta de Riemann. L hypothèse de Riemann est une conjecture formulée en 1859 par le mathématicien Bernhard Riemann. Elle dit que les zéros non triviaux de la fonction zêta de… … Wikipédia en Français
Neuvieme probleme de Hilbert — Neuvième problème de Hilbert Le neuvième problème de Hilbert est l un des vingt trois problèmes ouverts proposés comme défis du XXe siècle par David Hilbert au second congrès international de mathématiques en 1900. Il consiste à généraliser… … Wikipédia en Français
Neuvième Problème De Hilbert — Le neuvième problème de Hilbert est l un des vingt trois problèmes ouverts proposés comme défis du XXe siècle par David Hilbert au second congrès international de mathématiques en 1900. Il consiste à généraliser la loi de réciprocité… … Wikipédia en Français
Neuvième problème de hilbert — Le neuvième problème de Hilbert est l un des vingt trois problèmes ouverts proposés comme défis du XXe siècle par David Hilbert au second congrès international de mathématiques en 1900. Il consiste à généraliser la loi de réciprocité… … Wikipédia en Français
Seizième problème de Hilbert — Le seizième problème de Hilbert est l un des 23 problèmes de Hilbert. Il comporte deux parties. La première concerne le nombre de branches réelles (ovales) d une courbe algébrique, et leur disposition ; de nombreux résultats modernes… … Wikipédia en Français
Septieme probleme de Hilbert — Septième problème de Hilbert Le septième problème de Hilbert concerne l irrationalité et la transcendance de certains nombres (Irrationalität und Transzendenz bestimmter Zahlen). Dans sa formulation géométrique, il demande quand l assertion… … Wikipédia en Français
Septième problème de hilbert — Le septième problème de Hilbert concerne l irrationalité et la transcendance de certains nombres (Irrationalität und Transzendenz bestimmter Zahlen). Dans sa formulation géométrique, il demande quand l assertion suivante est démontrable :… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Troisième problème de hilbert