Groupe libre

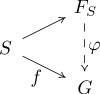
En théorie des groupes, le groupe libre sur un ensemble S est le groupe F contenant S et caractérisé par la propriété universelle suivante : pour tout groupe G et toute application f : S → G, il existe un unique morphisme de groupes de F dans G prolongeant f.

Soit encore, un groupe G est dit libre sur un sous-ensemble S de G si chaque élément de G s'écrit de façon unique comme produit réduit d'éléments de S et d'inverses d'éléments de S (réduit signifiant : sans occurrence d'un sous-produit de la forme x.x^-1). Un tel groupe est unique à isomorphisme près ce qui justifie le qualificatif le dans la définition. En général, on le notera F_S ou L(S). Intuitivement, F_S est le groupe engendré par S, sans relations entre les éléments de S autres que celles imposées par la structure de groupe.

Attention : cette notion diffère de celle de groupe abélien libre.

Histoire

Walther von Dyck étudie en 1882 le concept de groupe libre, sans y donner de nom, dans son article Gruppentheoretische Studien (Études en théorie des groupes) publié dans Mathematische Annalen. Le terme de groupe libre a été introduit en 1924 par Jakob Nielsen (en), qui a défini des transformations (en) qui engendrent le groupe d'automorphismes de ce groupe (en).

Construction

Introduisons un ensemble S' équipotent à S et disjoint de S. Il existe alors une bijection de S vers S'. Pour chaque élément s de S, on note s' l'élément correspondant dans S'.

Notons M l'ensemble des mots sur la réunion de S et de S', c'est-à-dire les chaînes finies de caractères constituées d'éléments de S et de S'. Deux telles chaînes seront dites équivalentes si on peut passer de l'une à l'autre en enlevant ou en rajoutant des chaînes de la forme ss' ou s's. Ceci définit une relation d'équivalence R sur M. On définit F_S comme l'ensemble des classes d'équivalence modulo R. On identifie chaque élément s de S avec sa classe dans F_S pour avoir l’inclusion .

La concaténation de deux mots définit une loi sur M préservée par l'équivalence. Par passage au quotient, on obtient un loi de groupe sur F_S. L'élément neutre est la classe du mot vide, et l'inverse de la classe de est la classe de .

Vérification de la propriété universelle : Si G est un groupe, toute application ensembliste se prolonge en un morphisme de monoïdes défini par . Ce morphisme est constant sur les classes d'équivalence, et induit donc un morphisme de groupes qui prolonge f.

Premières propriétés

• Si S et T ont même cardinalité, alors F_S et F_T sont isomorphes. En effet, une bijection entre S et T donne lieu à des morphismes de F_S dans F_T et de F_T dans F_S, morphismes qui sont réciproques l'un de l'autre. Réciproquement, si F_S et F_T sont isomorphes, on peut montrer que S et T ont même cardinal. D’ailleurs, si S est infini, F_S a le même cardinal que S.
• Soit G un groupe, et soit S une partie génératrice de G. Alors G est un quotient du groupe libre F_S sur S. En particulier, n’importe quel groupe est le quotient d'un groupe libre, d’où la notion de présentation d'un groupe (par générateurs et relations).
• Le foncteur objet libre (en) qui à tout ensemble S associe le groupe libre F_S est l'adjoint à gauche du foncteur d'oubli, de la catégorie des groupes dans celle des ensembles.
• Si S est de cardinal supérieur ou égal à deux alors F_S est non commutatif. En effet, pour tous distincts, par unicité de l'écriture.

Exemples

• Le groupe libre sur l'ensemble vide est le groupe trivial, et le groupe libre sur un singleton est isomorphe à .
• Soit n un entier naturel. Le groupe fondamental du plan privé de n points est un groupe libre sur un ensemble de cardinal n.

Sous-groupes d'un groupe libre

• D'après le théorème de Nielsen-Schreier, tout sous-groupe d'un groupe libre F_S est un groupe libre F_T, mais le cardinal de T n'est pas nécessairement inférieur ou égal à celui de S. Par exemple, dans le groupe libre F_{a,b} à deux générateurs, le sous-groupe engendré par les aⁿba ^{− n} (pour tous les entiers n) n’admet aucun système fini de générateurs : c'est groupe libre sur une infinité dénombrable de générateurs.
• Le groupe dérivé de F_{a,b} est lui aussi un groupe libre sur une infinité dénombrable de générateurs : les commutateurs [a^m,bⁿ] pour tous les entiers m,n non nuls.

Ainsi, même pour les sous-groupes distingués, on n’a pas d’analogue non abélien du résultat suivant : tout sous-groupe d'un groupe abélien libre est un groupe abélien libre dont le rang est un cardinal inférieur ou égal au rang du groupe.

Référence

(en) Marshall Hall, Jr. (en), The theory of groups [détail des éditions], chapitre 7

• Portail des mathématiques