Antecedent (mathematiques)
- Antecedent (mathematiques)
-
Antécédent (mathématiques)
Définition
En mathématiques, étant donnés deux ensembles non vides E, F et une application 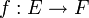 , on appelle antécédent (par f) d'un élément y de F tout élément x de E tel que
, on appelle antécédent (par f) d'un élément y de F tout élément x de E tel que 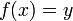 .
.
Un antécédent est donc, par définition, un élément de l'image réciproque 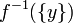 .
.
Exemples
- Soient la fonction
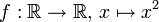 et y un réel.
et y un réel.
- Si y > 0, y admet deux antécédents, qui sont
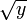 et
et 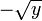
- Si y = 0, y admet un seul antécédent, qui est 0
- Si y < 0, y n'admet aucun antécédent
- Soient E un ensemble non vide, et une application
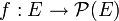 , où
, où 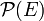 désigne l'ensemble des parties de E. On définit
désigne l'ensemble des parties de E. On définit 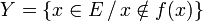 : Y est une partie de E, autrement dit un élément de l'ensemble
: Y est une partie de E, autrement dit un élément de l'ensemble 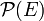 .
.
- Cet élément n'admet aucun antécédent par f. En effet, supposons qu'un tel antécédent
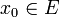 existe. On a donc
existe. On a donc 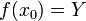 .
.
- Deux cas sont possibles :
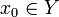 , ce qui veut dire (par définition de Y) que
, ce qui veut dire (par définition de Y) que 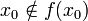 , ou
, ou 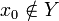
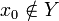 , ce qui veut dire (par définition de Y) que
, ce qui veut dire (par définition de Y) que 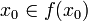 , ou
, ou 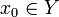
- Dans les deux cas, on aboutit à une contradiction, ce qui prouve par l'absurde que Y n'a pas d'antécédent (cf. l'argument de la diagonale de Cantor).
Image d'un ensemble par une application
Soient une application 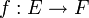 et A un sous-ensemble de E. On appelle image de A par f l'ensemble des éléments y de F qui admettent au moins un antécédent appartenant à A ; on la note
et A un sous-ensemble de E. On appelle image de A par f l'ensemble des éléments y de F qui admettent au moins un antécédent appartenant à A ; on la note 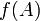 :
:
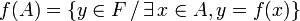 .
.
En particulier, l'image de E par f, appelée image de f, est l'ensemble des éléments y de F qui admettent au moins un antécédent :
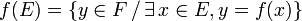 .
.
Injections, surjections, bijections
Soit une application 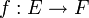 .
.
- On dit que f est injective, ou que c'est une injection, si tout élément de F admet au plus un antécédent.
- On dit que f est surjective, ou que c'est une surjection, si tout élément de F admet au moins un antécédent, c'est-à-dire si
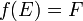 .
.
- On dit que f est bijective, ou que c'est une bijection, si tout élément de F admet un antécédent et un seul, c'est-à-dire si f est à la fois injective et surjective.
- Dans ce cas, on peut définir l'application
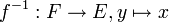 , où x est l'unique antécédent de y par f. C'est aussi une bijection, dite réciproque de f.
, où x est l'unique antécédent de y par f. C'est aussi une bijection, dite réciproque de f.
(l'exemple vu plus haut montre qu'il n'existe aucune application surjective 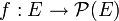 ).
).
Voir aussi
Catégorie : Théorie des ensembles
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Antecedent (mathematiques) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Antécédent (Mathématiques) — Pour les articles homonymes, voir Antécédent. Sommaire 1 Définition 1.1 Exemples 2 … Wikipédia en Français
Antécédent (mathématiques) — Pour les articles homonymes, voir Antécédent. En mathématiques, étant donnés deux ensembles E, F et une application , on appelle antécédent (par f) d un élément y de F tout élément dont l image par f est y, c est à dire tout élément x de E tel… … Wikipédia en Français
antécédent — antécédent, ente 1. (an té sé dan, dan t ) adj. Qui précède dans l ordre des temps. Des actes antécédents annulent celui ci. ÉTYMOLOGIE Antecedens, de ante, avant (voy. ains), et cedere, aller (voy. céder) ; provenç. anteceden ; … Dictionnaire de la Langue Française d'Émile Littré
Antecedent — Antécédent Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Antécédent — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Antécédent », sur le Wiktionnaire (dictionnaire universel) Le mot antécédent peut avoir plusieurs… … Wikipédia en Français
ANTÉCÉDENT, ENTE — adj. Qui précède dans l’ordre du temps. Les actes antécédents. Les procédures antécédentes. Il est très souvent employé comme nom masculin. Cet homme a de fâcheux antécédents, Ses actions, sa conduite antérieure sont blâmables. En termes de… … Dictionnaire de l'Academie Francaise, 8eme edition (1935)
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Application (mathématiques) — Pour les articles homonymes, voir Application. Pour les applications des mathématiques à d autres domaines, voir « Mathématiques appliquées » … Wikipédia en Français
Application (Mathématiques) — Pour les articles homonymes, voir Application. Graphique d une fonction … Wikipédia en Français
Application (mathematiques) — Application (mathématiques) Pour les articles homonymes, voir Application. Graphique d une fonction … Wikipédia en Français
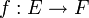 , on appelle antécédent (par f) d'un élément y de F tout élément x de E tel que
, on appelle antécédent (par f) d'un élément y de F tout élément x de E tel que 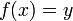 .
.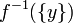 .
.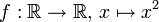 et y un réel.
et y un réel.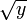 et
et 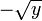
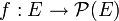 , où
, où 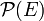 désigne l'ensemble des parties de E. On définit
désigne l'ensemble des parties de E. On définit 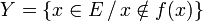 : Y est une partie de E, autrement dit un élément de l'ensemble
: Y est une partie de E, autrement dit un élément de l'ensemble 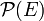 .
.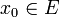 existe. On a donc
existe. On a donc 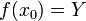 .
.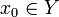 , ce qui veut dire (par définition de Y) que
, ce qui veut dire (par définition de Y) que 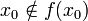 , ou
, ou 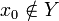
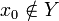 , ce qui veut dire (par définition de Y) que
, ce qui veut dire (par définition de Y) que 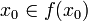 , ou
, ou 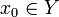
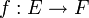 et A un sous-ensemble de E. On appelle image de A par f l'ensemble des éléments y de F qui admettent au moins un antécédent appartenant à A ; on la note
et A un sous-ensemble de E. On appelle image de A par f l'ensemble des éléments y de F qui admettent au moins un antécédent appartenant à A ; on la note 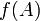 :
: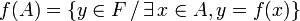 .
.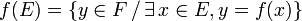 .
.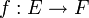 .
.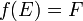 .
.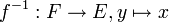 , où x est l'unique antécédent de y par f. C'est aussi une bijection, dite réciproque de f.
, où x est l'unique antécédent de y par f. C'est aussi une bijection, dite réciproque de f.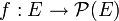 ).
).