- Fréquence de résonance
-
Résonance
 Cet article concerne la résonance en physique. Pour la station de radio, voir Resonance FM. Pour les structures de résonance en chimie, voir Mésomérie.
Cet article concerne la résonance en physique. Pour la station de radio, voir Resonance FM. Pour les structures de résonance en chimie, voir Mésomérie.La résonance est un phénomène selon lequel certains systèmes physiques (électriques, mécaniques...) sont sensibles à certaines fréquences. Un système résonant peut accumuler une énergie, si celle-ci est appliquée sous forme périodique, et proche d'une fréquence dite "fréquence de résonance" ou "fréquence naturelle" ou fréquence propre. Soumis à une telle excitation, le système va être le siège d'oscillations de plus en plus importantes, jusqu'à atteindre un régime d'équilibre qui dépend des éléments dissipatifs du système, ou bien jusqu'à une rupture d'un composant du système.
Si on soumet un système résonant à un degré de liberté non plus à une excitation périodique mais à une percussion (pour les systèmes mécaniques), ou à une impulsion (pour les systèmes électriques), alors le système sera le siège d'oscillations amorties, sur une fréquence dite fréquence propre et retournera progressivement à son état stable.
Les domaines où la résonance intervient sont innombrables : balançoire enfantine, mais aussi résonances acoustiques des instruments de musique, la résonance des marées, la résonance orbitale en astronomie, la résonance de la membrane basilaire dans le phénomène d'audition, les résonances dans des circuits électroniques et, pour finir tous les systèmes, montages, pièces mécaniques sont soumis au phénomène de résonance. Les systèmes abstraits sont également soumis à des résonances, par exemple la dynamique des populations.
Sommaire
Notions de base
Principe physique
Un système susceptible d'entrer en résonance, c'est à dire susceptible d'être le siège d'oscillations amorties, est un oscillateur. Un tel système a la particularité de pouvoir emmagasiner temporairement de l'énergie sous deux formes: potentielle ou cinétique. L'oscillation est le phénomène par lequel l'énergie du système passe d'une forme à l'autre, de façon périodique.
Par exemple, dans un système mécanique, l'énergie passe de la forme potentielle à la forme cinétique: Une corde vibrante aura son énergie sous forme entièrement potentielle au moment où elle passe par son maximum d'élongation. Au moment où la corde passe par sa position d'équilibre , sa vitesse est maximale, et son énergie est entièrement sous forme cinétique.
Dans un circuit LC, l'énergie est sous forme potentielle quand la tension est maximale aux bornes du condensateur. L'énergie est sous forme cinétique (ou magnétique) quand le courant est maximum dans la self ( et la tension nulle sur le condensateur).
Si on injecte une énergie potentielle au moment où l'énergie potentielle déjà emmagasinée est maximale , l'énergie ainsi injectée s'ajoute à l'énergie déjà emmagasinée et l'amplitude de l'oscillation va augmenter , ainsi que l'énergie totale. De la même façon, si on injecte de l'énergie cinétique au moment où l'énergie cinétique est maximale, l'énergie totale augmentera. Si on apporte ainsi de l'énergie avec une périodicité égale ( ou proche) de la périodicité propre du système, l'énergie totale va augmenter régulièrement. L'amplitude des oscillations du système va ainsi croître. L'exemple le plus simple est celui d'une balançoire : l'énergie de chaque poussée s'ajoute à l'énergie totale, à condition de pousser au bon moment...
Le phénomène de résonance n'est rien d'autre que cet effet d'accumulation de l'énergie en injectant celle-ci au moment où elle peut s'ajouter à l'énergie déjà accumulée, c'est à dire "en phase " avec cette dernière.
Amortissement
Quand l'excitation aura cessé, le système résonant va être le siège d'oscillations amorties: il va revenir plus ou moins vite à son état d'équilibre stable. En effet, l'énergie de départ sera peu à peu absorbée par les éléments "dissipatifs" du système ( amortisseur visqueux en mécanique, résistances en électricité...). Un système peu amorti sera le siège d'un grand nombre d'oscillations qui diminueront lentement avant de disparaître complètement.
Si on soumet un système peu amorti à une excitation périodique permanente selon sa fréquence de résonance, l'énergie ainsi apportée va s'accumuler lentement et se traduira par des oscillations de grande amplitude. En régime stabilisé, l'énergie apportée à chaque période est égale à l'énergie dissipée, ce qui explique la grande amplitude des oscillations du système peu amorti. L'énergie accumulée sera importante, mais un amortissement accru peut diminuer l'amplitude des oscillations, l'énergie dissipée par période et donc l'énergie accumulée.
En électricité, on peut chiffrer l'amortissement en définissant le "coefficient de surtension" ou la "sélectivité".
Modes propres
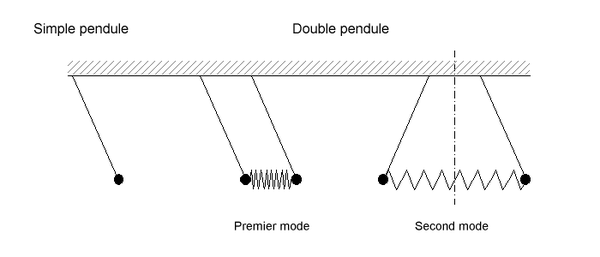
Implicitement, l'introduction concerne des systèmes à un degré de liberté ou supposés tels dont l'évolution est décrite par un seul paramètre fonction du temps. On rencontre de tels systèmes, entre autres, en mécanique avec le simple pendule ou le système masse-ressort, en électricité avec le circuit RLC. Leurs oscillations libres ne peuvent se produire qu'à une fréquence bien définie susceptible d'induire une résonance.
Si on couple deux pendules par un ressort, le système est alors décrit par les inclinaisons généralement distinctes des deux pendules. Ce système à deux degrés de liberté possède deux modes propres dans lesquels les pendules oscillent à la même fréquence. Toute oscillation libre est une somme des deux modes propres correspondants et, face à une excitation sinusoïdale, chacun d'eux peut engendrer une résonance. En supposant les deux pendules identiques, l'origine des deux types d'oscillation devient évidente. Dans un cas les pendules oscillent de concert, comme s'ils étaient liés par une barre rigide ; la fréquence propre du système est la même que celle du pendule simple. Dans l'autre, ils oscillent en opposition, comme si le milieu du ressort avait été fixé ; une moitié de ressort accroît donc la raideur associée à chacun d'eux, ce qui, comme il est précisé plus loin, augmente la fréquence propre.
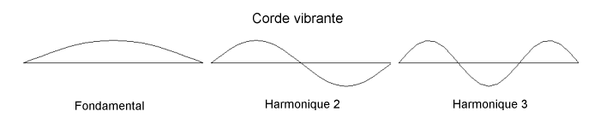
Ces remarques se généralisent à des systèmes qui possèdent un nombre quelconque de degrés de liberté. La déformée d'une corde vibrante ou d'une poutre élastique est caractérisée par une infinité de positions ; il s'agit alors de systèmes continus à une infinité de degrés de liberté possédant une infinité de modes propres. Dans le cas de la corde sans raideur en flexion, les modes propres ont des formes sinusoïdales (pour plus de précisions, voir Onde sur une corde vibrante. La plus basse fréquence est alors appelée fréquence fondamentale tandis que les harmoniques ont des fréquences multiples de celle-ci, le spectre est l'ensemble des fréquences propres.
 Animation : 3 premiers modes de vibration d'une corde
Animation : 3 premiers modes de vibration d'une corde
Généralement, l'importance relative de l'amortissement s'accroît à mesure que s'élève l'ordre des modes, ce qui fait qu'il est suffisant de s'intéresser aux tous premiers modes, dans les problèmes techniques si ce n'est en musique.
La représentation modale est pertinente dans le domaine des basses fréquences, c'est à dire pour les premiers modes propres (les modes sont classés traditionnellement par fréquences propres croissantes sur le spectre). Dans les domaines moyenne et haute fréquence,on utilise des méthodes adaptées à la densité spectrale élevée. Les domaines moyenne et fréquence et haute fréquence sont définis par la densité spectrale. En effet, l'expression en fréquences n'a pas de sens pour définir ces domaines, une similitude sur un système physique modifie les fréquences propres mais le spectre reste semblable, à un facteur près. Dans le cas de fréquences multiples, il existe un sous-espace propre donc les modes propres sont arbitraires dans ce sous espace. Dans le cas de fréquences voisines(densité spectrale élevée), la représentation modale n'est pas robuste car de faibles perturbations du domaine physique vont entraîner un changement important des modes propres associés à ces fréquences. Donc la représentation modale n'est pertinente que pour le domaine des basses fréquences, domaine définie par la densité spectrale. Le domaine basse fréquence s'étendra jusqu'à quelques Hz en génie civil, jusqu'à des milliers de Hz pour de petites structures mécaniques.
Réponse à une excitation
Dans un système oscillant à un degré de liberté, on constate que le rapport de l'amplitude X de la réponse à l'amplitude F de l'excitation dépend de la masse M (ou inertie ou, en électricité, auto-inductance), de la raideur K (ou inverse de la capacité) et de l'amortissement B (ou résistance) :
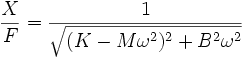
Cette formule montre, ce qui se généralise qualitativement à des systèmes beaucoup plus complexes, voire non-linéaires, que la fréquence propre croît avec la raideur et décroît lorsque l'inertie augmente.
Quantitativement, pour un système linéaire, la généralisation se ferait en définissant un effort généralisé, en projetant les efforts extérieurs sur le mode concerné. Un mode n'est pas excitable sur les nœuds de vibration.
L'amplification ne varie pas seulement en fonction de la fréquence. Elle dépend également de l'amortissement du système : lorsque celui-ci décroît, l'amplification augmente dans une bande de fréquences de plus en plus étroite.
Ce phénomène d'amplification est mis à profit dans divers domaines pour séparer une fréquence déterminée de ses voisines.
À l'inverse, il peut être fréquemment à l'origine de dommages causés au système. Dans ce dernier cas, on cherche soit à l'atténuer en augmentant l'amortissement, soit à déplacer la fréquence propre en jouant sur l'inertie ou sur la raideur.
La synchronisation
Huyguens a remarqué que deux horloges à balancier, placées sur la même cloison, synchronisaient leur mouvement, il fournit l'explication. Le système composé des deux balanciers et de la cloison a deux fréquences voisines faiblement couplées , il possède par le couplage deux modes propres correspondant aux mouvements en phase et en opposition de phase des deux pendules: c'est sur le premier mode que se produit la synchronisation. On retrouve la synchronisation dans de nombreux phénomènes naturels: vols d'oiseau , clignotement des lucioles...
Utilisations de la résonance
La résonance permet de trier certaines fréquences, mais ne produit pas d'énergie. Le résonateur accumule de l'énergie.
Le moteur deux temps
Le pot d'échappement d'un moteur deux temps a une forme bien particulière, calculée pour créer un phénomène de résonance ; Résonance qui améliore les performances du moteur : en diminuant la consommation et la pollution. Cette résonance réduit partiellement les gaz imbrulés et augmente la compression dans le cylindre.
Les instruments de musique
Pour ce qui est des instruments à cordes frottées et à vent, la production du son consiste la plupart du temps en l'excitation d'un système oscillant (corde, colonne d'air) jusqu'à l'apparition d'un phénomène de résonnance.
Les récepteurs radio
Chaque station émet une onde électromagnétique avec une fréquence bien déterminée. Pour la capter, le circuit RLC (résistance, inductance, capacité) est mis en vibration forcée, par l'intermédiaire de l'antenne qui capte toutes les ondes électromagnétiques arrivant jusqu'à elle. Pour écouter une seule station, on doit accorder la fréquence propre du circuit RLC avec la fréquence de l'émetteur désiré, en faisant varier la capacité d'un condensateur variable (opération effectuée en agissant sur le bouton de recherche des stations).
D'une façon générale, tous les systèmes de radiocommunications, qu'ils soient émetteur ou récepteur, utilisent des résonateurs pour "filtrer" les fréquences des signaux qu'ils traitent: Circuit RLC, résonateurs à quartz, résonateurs céramique, etc...
L'imagerie par résonance magnétique
En 1946, les deux américains Félix Bloch et Edward Mills Purcell découvrent le phénomène de Résonance Magnétique Nucléaire également appelée RMN (ce qui leur valut un prix Nobel de Physique). En plaçant un objet ou un tissu organique quelconque dans un champ magnétique, on peut connaître grâce à un signal qu’émet cet objet, sa constitution.
En 1971, Raymond Damadian se rend compte que le signal émis par un tissu organique cancéreux est différent de celui qu’émet un tissu sain du même organe. Deux ans plus tard, Paul Lauterbur traduit le signal en images à deux dimensions. Apparaît alors l’imagerie par résonance magnétique proprement dite, créée à partir de séquences pondérées T1 et T2 émettant respectivement un signal noir ou blanc.
L’IRM subira encore quelques évolutions : le britannique Peter Mansfield applique la RMN des objets à structure interne complexe. Il deviendra grâce à ses expériences poussées, l’un des pionniers de l’Imagerie par Résonance Magnétique dans des applications médicales. Par la suite, en 1971, Richard Ernst sera primé pour son travail « Spectroscopie à haute résolution par l’IRM » suivi du suisse Kurt Wüthrich en 2002 pour sa présentation « Imagerie en 3D des macromolécules en solution ».
L’IRM telle qu’on la connaît aujourd’hui après 60 ans d’histoire n’a pas fini son évolution et de nombreux progrès viendront encore. C’est grâce à une physique complexe et développée que l’IRM a su apporter aux sciences (en particulier en médecine) un nouveau moyen de progresser.
Fonctionnement simplifié de l'IRM
L'IRM utilise la résonance des protons d'un organisme pour fabriquer des images. Les protons des molécules d'eau réagissent de façon spécifique au champ magnétique ; le corps humain est composé en majorité d'eau. Placé dans un intense champ magnétique, on excite les protons des molécules d'eau à l'aide d'une émission électromagnétique (radio-fréquence) jusqu'à les mettre en résonance. Avec une antenne, on mesure l'énergie rendue par les protons lors de l'arrêt de l'excitation. Un puissant ordinateur analyse et interprète les informations captées par l'antenne, en créant une image en trois dimensions.
Inconvénients de la résonance
Automobiles
Les automobilistes sont souvent irrités par les bruits parasites qui apparaissent à une certaine vitesse du véhicule ou de rotation du moteur. Certaines pièces mal amorties du moteur, ou de la carrosserie, entrent en résonance et émettent des vibrations sonores. L'automobile elle-même, avec son système de suspension, constitue un oscillateur heureusement muni d'amortisseurs efficaces qui évitent que le véhicule n'entre en résonance aiguë.
Le dessin des pneumatiques est parfois périodique. De ce fait le roulement produit un bourdonnement. Sur certains pneumatiques le dessin peut être légèrement déphasé pour atténuer ce phénomène.
Les vagues engendrent des mouvements oscillatoires des navires. Sur un navire libre, faute de raideur, les mouvements linéaires selon les trois directions ne peuvent être soumis à la résonance et il en va de même pour le lacet. Restent le roulis et le tangage, ce dernier étant assez amorti pour ne pas être critique. Malheureusement la période propre de roulis tombe en général dans les périodes de vagues, le mouvement étant par ailleurs assez peu amorti. La meilleure solution pour lutter contre ce phénomène consiste à éviter de prendre les vagues par le travers. Il est également possible d'augmenter l'amortissement en ajoutant à la coque des appendices nommés quilles de roulis.
Sur les navires amarrés au large apparaît un autre phénomène, plus subtil, la dérive lente. En général, le système navire-amarrage a une période propre qui s'exprime en minutes. Elle ne peut donc être excitée par les vagues qui contiennent des périodes allant de quelques secondes à quelques dizaines de secondes mais l'excitation provient de termes non-linéaires. Ceux-ci créent de nouvelles fréquences sommes et différences de celles que contiennent les vagues, conformément à la formule de trigonométrie sur le produit de cosinus. Les forces correspondantes sont très petites mais, l'amortissement étant lui même très faible, la résonance induit des mouvements qui peuvent déplacer d'une ou deux dizaines de mètres un navire de quelques centaines de milliers de tonnes.
Génie Civil
Ponts
Un pont peut effectuer des oscillations verticales, transversales ou de torsion. À chacun de ces types d'oscillations, correspond une période propre, si le tablier est suspendu (maintenu par des câbles accrochés aux piliers), le système a une fréquence de résonance bien différente.
En 1850, une troupe traversant en ordre serré le pont de la Basse-Chaîne, pont suspendu sur la Maine à Angers, provoqua la rupture du pont par résonance et la mort de 226 soldats. Pourtant, le règlement militaire interdisait déjà de marcher au pas sur un pont, ce qui laisse à penser que ce phénomène était connu auparavant.
En 1940, de forts vents (de 65 à 80 km/h) provoquèrent la chute du pont de Tacoma Narrows (États-Unis). Des vibrations de flexion transversale amenèrent la rupture d'un câble, puis du reste de l'œuvre. La première explication fournie s'appuyait sur l'excitation d'une résonance par le détachement périodique de tourbillons dans une allée de Karman. En fait, la fréquence observée des vibrations était très inférieure à la fréquence de détachement qu'il est possible de calculer. Il sembla donc qu'il fallut abandonner, dans ce cas, l'explication par une résonance pour la remplacer, par celle qui fait appel à la notion d'instabilité aéroélastique. Dans un système linéaire possédant au moins une fréquence propre, comme ceux qui ont été envisagés précédemment, la stabilité est assurée quand le système est dissipatif, ou à la limite conservatif. Ici, le système devient actif, dans un vent que l'on peut supposer constant, à mesure que le tablier se tord, le moment des efforts aéroélastiques peut être approché par sa composante en phase avec le déplacement (pseudo-raideur) et sa composante en quadrature, proportionnelle à la vitesse de vibration. Dans le couplage d'une structure avec un fluide léger, les efforts aéroélastiques sont négligeables devant les forces d'inertie ou les efforts élastiques de la structure, sauf au voisinage des fréquences car ceux-ci s'y compensent. La composante en quadrature, quand elle s'oppose à l'amortissement traduit l'apport d'énergie éolienne à la structure, cause de l'instabilité aéroélastique. Le mode de torsion devient instable, ce qui correspond à des oscillations d'amplitude croissante. La rupture peut alors survenir. L'instabilité se produit toujours au voisinage d'un mode propre et donc d'une fréquence propre dans le couplage fluide léger-structure, cas des problèmes d'aéroélasticité que l'on rencontre aussi sur les avions, sur les moteurs d'avion...
Le pont fut reconstruit en tenant compte de ce problème et est toujours en place.
Voir en anglais http://www.vibrationdata.com/Tacoma.htm.
La passerelle du millénium a été construite à Londres pour l'an 2000.Elle dut être modifiée suite à un problème d'instabilité latérale engendré par le couplage de la marche des piétons avec le premier mode latéral.
http://en.wikipedia.org/wiki/Millennium_Bridge_%28London%29
Un phénomène analogue fut rencontré à Paris à la même époque avec la passerelle Solférino.
Chemins de fer
La construction ferroviaire rencontre aussi des problèmes liés à la résonnance. Les fils suspendus aux caténaires constituent des oscillateurs liés entre eux. Afin d'éviter qu'ils se transmettent l'onde du au contact avec les trains, les caténaires ne sont pas disposés à égales distance. Il en est de même pour les rails posés sur les traverses, mais le phénomène est observable pour des fréquences plus élevées.
Bâtiments
Les grands buildings sont sensibles aux tremblements de terre. Certains dispositifs passifs permettent de les protéger: il s'agit d'oscillateur (gros pendule suspendu en haut de l'immeuble) dont la fréquence propre est voisine de celle du bâtiment lui même. Ainsi l'energie est totalement absorbée par le pendule empêchant l'immeuble de se briser.
Résonances marines
Les ports sont le lieu d'ondes stationnaires de périodes bien définies appelées seiches. Dans certains sites, ces ondes peuvent être excitées par les trains de vagues, créant ainsi des oscillations horizontales qui peuvent être dommageables pour les bateaux amarrés.
Un phénomène analogue, à plus grande échelle, s'observe dans les golfes, l'excitation étant fournie par les ondes de marée. Il ne présente pas d'inconvénients particuliers et peut même être utilisé par des usines marémotrices.
Voir aussi
Articles connexes
- Résonance acoustique
- Circuit RLC
- Phénomène de Résonance sur le Tacoma Narrows Bridge
- Pendule simple
- Système oscillant à un degré de liberté
- oscillateur
- espace des phases
Liens externes
- L'imagerie par résonance magnétique
- Une vidéo explicative sur la résonance entre pendules
- Une vidéo explicative sur la résonance dans un circuit RLC
- Site expliquant la résonance magnétique dans le cas de l'IRM
- Portail de la physique
- Portail du monde maritime
Catégories : Concept fondamental de la physique | Systèmes oscillants
Wikimedia Foundation. 2010.