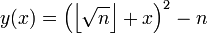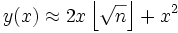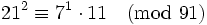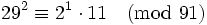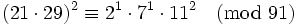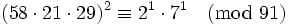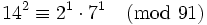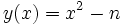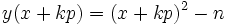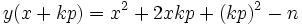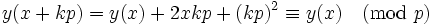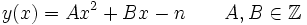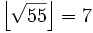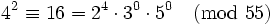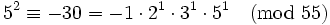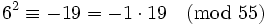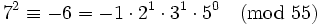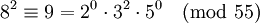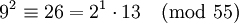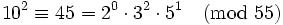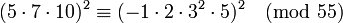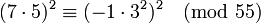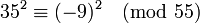Crible Quadratique

L'algorithme crible quadratique (QS pour Quadratic sieve) est un algorithme moderne de décomposition en produit de facteurs premiers fondé sur l'arithmétique modulaire. Dans la pratique, la seconde méthode connue la plus rapide. C'est un algorithme de factorisation à but général, ce qui veut dire que son temps d'exécution dépend uniquement de la taille de l'entier à factoriser, et non d'une structure spéciale ou des propriétés de celui-ci.

Sommaire 1 Objectif de base 2 Comment QS optimise la recherche de congruences 2.1 Relations partielles et cycles 2.2 Vérifier la régularité par criblage 3 Polynômes multiples 4 Exemple 4.1 Collecte des données 4.2 Calcul des données 5 Records de factorisation

Objectif de base

L'algorithme essaye d'établir une congruence de carrés modulo n (l'entier à factoriser), qui, souvent, conduit à une factorisation de n. L'algorithme fonctionne en deux phases : la phase de collecte des données, où il collecte les informations qui peuvent conduire à une congruence de carrés ; et la phase de calcul des données, où il place toutes les données qu'il a collectées dans une matrice et la résout pour obtenir une congruence de carrés. Cette phase requiert une grande quantité de mémoire et ne peut pas être mise en parallèle et donc, elle est habituellement exécutée par un supercalculateur quand le nombre à factoriser a plus de 100 chiffres.

L'approche naïve pour trouver une congruence de carrés est de prendre un nombre aléatoire, l'élever au carré, et espérer que le plus petit reste non-négatif modulo n est un carré parfait. Cette approche trouve rarement une congruence de carrés pour les grands n, mais lorsqu'une est trouvée, plus souvent qu'on ne le pense, la factorisation est complète.

Le crible quadratique est une modification de la méthode de factorisation de Dixon.

Comment QS optimise la recherche de congruences

Le crible quadratique essaie de trouver des paires d'entiers x et y(x) (où y(x) est une fonction de x satisfaisant à la condition plus faible que x² ≡ y² (mod n). Il sélectionne une borne régulière B, et essaie de trouver x tel que le plus petit reste absolu de x² mod n (y(x)) est B-régulier. Une telle paire d'entiers est appelée une relation. L'ensemble des nombres premiers inférieurs ou égaux à B est appelé la base des facteurs.

Le crible quadratique accélère le processus de recherche de relations en prenant x fermé par la racine carrée de n. Ceci assure que y(x) sera plus petit, et ainsi a une chance plus grande d'être B-régulier. (x étant un petit entier) :

Ceci implique que y est d'ordre 2x[√n]. Néanmoins, cela implique aussi que y croît linéairement avec le carré de |x|.

Nous pouvons aussi augmenter les chances de régularité en augmentant simplement la taille de la base des facteurs, mais cela veut dire que nous avons à collecter plus de relations. Nous devons avoir au moins autant de relations que nous avons de nombres premiers dans la base des facteurs.

Relations partielles et cycles

Même si nous trouvons une relation où y(x) n'est pas B-régulier, nous pouvons être capable de fusionner deux de ces relations partielles pour en former une complète. Ceci n'est seulement possible que si deux y sont les produits des mêmes nombres premiers en dehors de la base de facteurs. Par exemple, si B = 7 et n = 91, nous avons les relations partielles :

Nous pouvons les multiplier ensemble :

et multiplier les deux cotés par (11⁻¹)² modulo 91. 11⁻¹ = 58, donc :

et nous avons une relation complète. Une telle relation complète (obtenue par combinaison de relations partielles) est appelée un cycle. Quelquefois, la formation d'un cycle à partir de deux relations partielles conduit directement à une congruence de carrés, mais rarement.

Vérifier la régularité par criblage

Il existe plusieurs manières de vérifier la régularité des y. La plus évidente est la méthode des essais de divisions, bien que ceci augmente le temps d'exécution pour la phase de collecte des données. Une autre méthode pouvant être admise est la méthode de la courbe elliptique. Néanmoins, dans la pratique, un processus appelé criblage est utilisé.

Ansi, en résolvant y(x) ≡ 0 (mod p) pour p, nous trouvons une suite entière de y qui sont divisibles par p. (c'est la raison du nom de ce crible -- y est un polynôme quadratique en x, et le processus de criblage fonctionne comme le Crible d'Ératosthène.) En répétant ce processus pour d'autres valeurs de p, cela nous permet de trouver rapidement de bonnes valeurs B-régulières, sans avoir à tester la régularité à chaque fois. Lorsque de grandes bases de facteurs sont utilisées (voir les records de factorisation ci-dessous), disons 500 000 nombres premiers, le test de régularité à chaque fois prend trop de temps pour être pratique.

Lorsque la phase de calcul des données commence, il est néanmoins nécessaire de factoriser les valeurs y collectées, comme nous avons besoin de savoir les exposants associés à chaque nombre premier de la base des facteurs. Ceci ne consomme pas de temps comme le test de régularité par factorisation, comme nous connaissons déjà par quels nombres premiers une valeur y est divisée, à partir du criblage.

Polynômes multiples

Dans la pratique, beaucoup de polynômes différents sont utilisés pour y, comme avec un seul polynôme, nous ne pourrons pas collecter assez de paires (x, y) qui sont régulières sur la base des facteurs. Les polynômes doivent tous avoir une forme similaire à l'original y(x) = x² − n:

Cette approche (appelée MPQS, Multiple Polynomial Quadratic Sieve (crible quadratique à polynômes multiples)) est adaptée idéalement aux parallèlisation, comme chaque processeur impliqué dans la factorisation peut recevoir un n donné, la base de facteurs et une collection de polynômes, il n'aura pas besoin de communiquer avec le processeur central jusqu'à ce qu'il ait fini avec ses polynômes.

Exemple

Voici un exemple. Soit n = 55 et B = 5. Comme n est petit (très petit, même !), nous avons seulement besoin d'un polynôme, et pas de criblage.

Collecte des données

Maintenant, nous avons x egal à ...−2, −1, 0, 1, 2... et nous vérifions si le y résultant est 5-régulier. Gardons à l'esprit que −1 est inclus dans la base des facteurs.

Nous avons à collecter, au minimum, une relation complète en plus de la quantité de nombres premiers présents dans la base des facteurs pour garantir la présence d'une congruence de carrés. Nous avons maintenant 4 relations complètes, avec 4 nombres premiers dans la base des facteurs. En fait, c'est un résultat standard issu de l'algèbre linéaire où nous avons besoin de t + 1 relations complètes indépendantes pour garantir une dépendance linéaire (un rapport qui produira une congruence de carrés), où t est la taille de la base des facteurs. Lorsque t est grand, il est presque impossible que les relations soient indépendantes, donc, nous calculons plus de relations complètes pour pouvoir contourner ce problème.

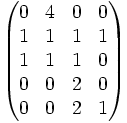
y(6) et y(9), où nous pensons qu'elles contiennent toutes les deux de grands nombres premiers, contiennent des grands nombres premiers différents et donc, ne peuvent pas être combinées en une relations complète. Nous pouvons entrer les vecteurs exposants (vecteurs lignes qui listent les exposants qui élèvent chaque nombre premier respectifs) dans une matrice. Chaque colonne représente un des nombres premiers de notre base de facteurs ; à partir de la gauche vers la droite : −1, 2, 3, 5. Nous listons seulement les « bonnes » paires, c.est-à-dire ceux qui sont 5-réguliers.

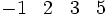
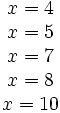
Calcul des données

En utilisant l'algèbre linéaire, nous pouvons trouver des lignes qui, lorsqu'elles sont ajoutées ensemble, produisent un vecteur ligne avec toutes ses entrées paires. Dans ce cas, la matrice est suffisamment petite pour que nous puissions trouver simplement de telles lignes par inspection. En fait, les lignes correspondantes à x = 4 et x = 8 sont déjà des congruences de carrés, mais nous indiquerons des relations combinées pour obtenir une congruence, cependant. En ajoutant les lignes x = 5, 7, et 10 nous aurons le vecteur entièrement pair (2 2 4 2). Nous multiplions ces relations ensemble et nous obtenons :

Ainsi, nous avons notre congruence de carrés. Maintenant, pgcd(35 − 9, 55) = 1, et pgcd(35 + 9, 55) = 11. Si nous n'avions pas annulé 10 dans la deuxième ligne, nous aurions eu pgcd(350 − 9) = 5 et gcd(350 + 90, 55) = 55. N'importe quelle approche produit un facteur non-trivial de 55.

Cette démonstration pourrait aussi servir à montrer que le crible quadratique est seulement approprié lorsque n est grand. Pour un nombre aussi petit que 55, cet algorithme fait du matraquage. Les essais de divisions pourraient trouver un facteur avec 3 divisions.

Records de factorisation

Jusqu'à la découverte du crible de corps de nombres (NFS), QS fut l'algorithme à but général le plus rapide asymptotiquement connu. Maintenant, la factorisation en courbe elliptique de Lenstra possède le même temps d'exécution asymptotique que QS (dans le cas où n possède exactement deux facteurs premiers de taille égale), mais dans la pratique, QS est plus rapide car il utilise des calculs en simple précision à la place des calculs en multi-précision utilisés par la méthode de la courbe elliptique.

Le 2 avril 1994, la factorisation de RSA-129 fut accomplie en utilisant QS. C'était un nombre de 129 chiffres, et le produit de deux grands nombres premiers, dont l'un était d'une taille de 64 chiffres et l'autre, de 65 chiffres. La base des facteurs pour cette factorisation contenait 524 339 nombres premiers. La collection de données a pris 5 000 années mips, faite par calcul distribué par Internet. Les données collectées totalisèrent 2 Go. La phase de calcul des données a pris 45 heures sur un supercalculateur MasPar de Bellcore (massivement parallèle). Ceci fut la plus grande factorisation par algorithme à but général publiée, jusqu'à ce que NFS fut utilisé pour factoriser RSA-130, accomplie le 10 avril 1996. Tous les nombres RSA factorisés depuis lors l'ont été en utilisant NFS.

• Portail des mathématiques