- Factorisation En Courbe Elliptique De Lenstra
-
Factorisation en courbe elliptique de Lenstra
La factorisation de Lenstra (par les courbes elliptiques) est un algorithme probabiliste rapide pour la décomposition en produit de facteurs premiers qui emploie les courbes elliptiques.
Cette méthode fut le meilleur algorithme pour la décomposition en produit de facteurs premiers jusqu'au développement du crible général de corps de nombres (GNFS). Il est encore le meilleur pour l'extraction des diviseurs dont la taille ne dépasse pas 20 chiffres (64 bits), comme son temps d'exécution dépend de la taille d'un facteur p plutôt que de la taille du nombre n à factoriser.
C'est une amélioration de la traditionnelle méthode de factorisation p −1 de Pollard. Dans cette méthode, il était supposé que le nombre donné n possède un facteur premier p tel que p-1 possède seulement des « petits » facteurs premiers (les nombres dont les facteurs premiers sont tous « petits » sont dits friables). Alors, par le petit théorème de Fermat, ae=1 mod p si p-1 divise e et p ne divise pas a. En prenant e comme un produit de petits nombres premiers élevés aux petites puissances, et a comme un résidu aléatoire mod n, nous pouvons espérer factoriser n en calculant le PGCD de n et ae-1, comme les autres diviseurs q de n ne semblent pas avoir la propriété q-1 divise e - les valeurs friables sont rares. Néanmoins, l'on ne pourra pas factoriser n si n n'a pas un facteur premier p avec p-1 friable.
La factorisation de Lenstra contourne cet obstacle en considérant le groupe d'une courbe elliptique aléatoire sur le corps fini Fp, plutôt que sur le groupe multiplicatif de Fp qui a toujours un ordre p-1. L'ordre du groupe d'une courbe elliptique sur Fp varie entre
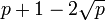et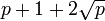 
(un théorème de Helmut Hasse) aléatoirement, et doit être probablement friable pour certaines courbes elliptiques.L'algorithme de factorisation de Lenstra permettant de trouver un facteur d'un nombre donné n fonctionne de la manière suivante :
- Prendre une courbe elliptique aléatoire sur Z avec un point A sur elle. Alors, nous considérons la loi de groupe sur cette courbe mod n - ceci est possible comme la plupart des résidus mod n ont des inverses, qui peuvent être trouvés en utilisant l'algorithme d'Euclide et en trouvant un résidu non-inversible équivalent à la factorisation de n
- Calculer eA dans ce groupe, où e est le produit de petits nombres premiers élevés aux petites puissances, comme dans la factorisation p−1 de Pollard. Il peut donner un nombre premier en une fois, et est ainsi efficace.
- Avec un peu de chance, eA est l'élément zéro du groupe de la courbe elliptique dans F p, mais pas dans F q pour un autre diviseur premier q de n (comme dans la méthode p−1 de Pollard, il est invraisemblable que les deux groupes auront un ordre qui est un diviseur de e). Alors nous pouvons trouver un facteur de n en trouvant le PGCD de la première coordonnée de A et n, comme cette coordonnée sera zéro dans F p.
- Si cela ne marche pas, il suffit de recommencer avec une autre courbe et/ou un autre point de départ.
Portail des mathématiques
Catégorie : Algorithme de factorisation des entiers
Wikimedia Foundation. 2010.
