- Essais de divisions
-
Divisions successives
En arithmétique modulaire, Les essais de divisions sont la technique la plus simple et la plus facile pour comprendre les algorithmes de factorisation de nombres entiers.
Soit un entier composé donné n (dans cet article, n veut dire « l'entier à factoriser »), les essais de divisions consistent à essayer de diviser n par chaque nombre premier inférieur ou égal à
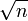. Si un nombre est trouvé et qu'il se divise de façon égale en n, un facteur de n a été trouvé.Les essais de divisions sont assurés de trouver un facteur de n, comme on vérifie tous les facteurs premiers possibles de n. De cette façon, si l'algorithme échoue, c'est la preuve que n est premier.
Les essais de divisions peuvent être optimisés de quelques façons. Par exemple, si le dernier chiffre de n n'est pas 0 ou 5, l'algorithme peut éviter le test du facteur 5. Le même argument peut être appliqué à 2 par vérification du dernier chiffre, et 3 par la vérification de la somme des chiffres. Pour plus de précisions, voir les critères de divisibilité.
Dans le pire des cas, les essais de divisions sont un algorithme inefficace. S'il commence à partir de 2 et se termine à la racine carrée de n, l'algorithme requiert
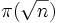
essais de divisions, où π(x) est la quantité de nombres premiers inférieurs à x. Ceci ne tient pas compte de l'étendue du test de primalité. Si une variante est utilisée sans test de primalité, mais simplement en divisant chaque nombre impair inférieurs à la racine carrée de n, premier ou non, il prend
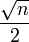essais de divisions. Ceci veut dire que pour un n avec de grands facteurs premiers d'une taille similaire (comme ceux utilisés pour les clés de cryptographie asymétrique), factoriser n par des essais de division requiert un nombre d'opérations rédhibitoire.Néanmoins, pour n avec au moins un petit facteur, les essais de divisions peuvent être une manière rapide de trouver ce petit facteur. Pour un n aléatoire, il existe 50 % de chances que 2 soit un facteur de n, et 33 % de chances que 3 soit un facteur, et ainsi de suite. Il peut être montré que 88 % de tous les entiers positifs ont un facteur inférieur à 100, et que 91 % ont un facteur inférieur à 1 000.
Pour des factorisations plus significatives, néanmoins, d'autres algorithmes sont plus efficaces.
Catégories : Algorithme de factorisation des entiers | Divisibilité et factorisation
Wikimedia Foundation. 2010.
