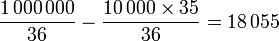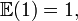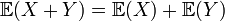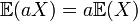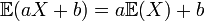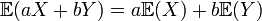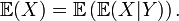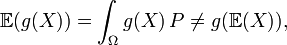Espérance Mathématique

Espérance mathématique

L'espérance mathématique est, en probabilités, une valeur numérique permettant d'évaluer le résultat moyen d'une expérience aléatoire.

Elle permet par exemple de mesurer le degré d'équité d'un jeu de hasard; elle est alors égale à la somme des gains (et des pertes) pondérés par la probabilité du gain (ou de la perte).

Exemple de la roulette française : en jouant un numéro plein, vous avez 1 chance sur 37 (les numéros vont de 0 à 36) de repartir avec 35 fois votre mise initiale^[1]. En misant 10 euros, votre espérance de gain est donc :

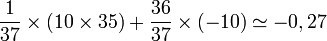$\frac{1}{37}\times (10\times 35)+\frac{36}{37}\times (-10) \simeq -0,27$ (les 10 euros de mise sont perdus avec une probabilité égale à 36/37).

Ce résultat indique qu'en moyenne, vous perdrez 27 centimes à chaque partie au profit du casino. Lorsque l'espérance est égale à 0, le jeu est dit équitable.

Sommaire

1 Espérance mathématique et choix rationnel
2 Incidence de la prime de risque
3 Applications particulières (économie, assurance, finance, jeux)
4 Notion d'utilité probabiliste
5 Aspect mathématique
6 Notes et références
7 Liens externes

Espérance mathématique et choix rationnel

Dans certains cas, les indications de l'espérance mathématique ne coïncident pas avec un choix rationnel. Imaginons par exemple qu'on vous fasse la proposition suivante : si vous arrivez à faire un double six avec deux dés, vous gagnez un million d'euros, sinon vous perdez 10 000 euros. Il est probable que vous refuserez de jouer. Pourtant l'espérance de ce jeu vous est très favorable : la probabilité de tirer un double 6 est de 1/36; on obtient donc :

$\frac{1\,000\,000}{36} - \frac{10\,000 \times 35}{36} = 18\,055$

à chaque partie vous gagnez en moyenne 18 000 euros.

Le problème tient justement sur ce « en moyenne » : si les gains sont extrêmement importants, ils n'interviennent que relativement rarement, et pour avoir une garantie raisonnable de ne pas finir ruiné, il faut donc avoir suffisamment d'argent pour participer à un grand nombre de parties. Si les mises sont trop importantes pour permettre un grand nombre de parties, le critère de l'espérance mathématique n'est donc pas approprié.

Incidence de la prime de risque

Ce sont ces considérations de risque de ruine qui conduisirent, à partir de son « paradoxe de Saint Petersbourg », le mathématicien Daniel Bernoulli à introduire en 1738 l'idée d'aversion au risque qui conduit à assortir l'espérance mathématique d'une prime de risque pour son application dans les questions de choix.

Applications particulières (économie, assurance, finance, jeux)

La notion de prime de risque appliquée à l'espérance mathématique fut en économie à l'origine du concept d'utilité (et d'utilité dite « marginale »).
les primes d'assurance sont d'un coût supérieur à l'espérance mathématique de perte du souscripteur du contrat. Mais c'est ce risque de forte perte en cas d'évènement rare qui l'incite à le souscrire.
L'espérance mathématique, comme d'autres concepts probabilistes, est utilisée dans les calculs d'évaluation en finance, par exemple pour l'évaluation d'entreprise.
La finance comportementale aborde, entre autres, les aspects émotionnels et cognitifs, qui vont au-delà de la simple prime de risque, et qui peuvent interférer avec le concept rationnel d'espérance mathématique à l'heure du choix.
De même que l'on paye une prime pour éviter le risque avec les assurances, on paie au contraire un accès au risque dans les jeux de hasard (qui rapportent toujours moins que leur espérance mathématique, puisqu'ils doivent s'autofinancer)

Notion d'utilité probabiliste

Plutôt que de passer par une notion de prime, on peut directement établir une fonction d'utilité, associant à tout couple {gain, probabilité} une valeur. L'espérance mathématique constitue alors la plus simple des fonctions d'utilité, appropriée dans le cas d'un joueur neutre au risque disposant de ressources au moins très grandes à défaut d'infinies.

Émile Borel adopta cette notion d'utilité pour expliquer qu'un joueur ayant peu de ressources choisisse rationnellement de prendre un billet de loterie chaque semaine : la perte correspondante n'est en effet pour lui que quantitative, tandis que le gain - si gain il y a - sera qualitatif, sa vie entière en étant changée. Une chance sur un million de gagner un million peut donc valoir dans ce cas précis bien davantage qu'un euro.

Aspect mathématique

L'espérance mathématique d'une variable aléatoire est l'équivalent en probabilité de la moyenne d'une série statistique en statistiques. Elle se note E(X) et se lit espérance de X.

L'espérance se calcule, comme la variance, à partir des moments d'une variable aléatoire.

Formules

L'espérance est définie pour les variables aléatoires à valeurs dans R (ou C) de la manière suivante :

Cas d'une variable discrète :
- Si X prend un nombre fini n de valeurs réelles : x₁, x₂, ..., x_n avec les probabilités p₁, p₂, ..., p_n alors
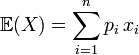
  $\mathbb E(X) = \sum_{i=1}^{n}p_i\, x_i$
- Si X prend un nombre dénombrable de valeurs réelles : x₀, x₁, ..., x_i, .... avec les probabilités p₀, p₁, ..., p_i, .... alors
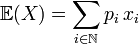  $\mathbb{E}(X) = \sum_{i \in \mathbb{N}}p_i\, x_i$ si la série converge absolument.

(la convergence absolue assure que la division de la série ne dépend pas de la manière de numéroter les termes)

Cas d'une variable à densité de probabilité :
- Si X a pour densité de probabilité f alors
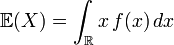  $\mathbb{E}(X) = \int_{\mathbb{R}} x\, f(x)\, dx$ à condition que cette intégrale existe.
Cas d'une application mesurable sur un espace de probabilité
- Si X est une application mesurable de (Ω, B, p) dans R, positive ou P-mesurable,
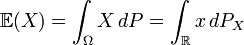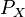  $\mathbb E(X) = \int_{\Omega}X\, dP = \int_{\mathbb{R}}x\, dP_X$ (où $\ P_X$ est la probabilité image).

Propriétés

Constantes

L'espérance d'une variable aléatoire constante est égale à cette constante; par exemple, si b est une constante, alors E(b) = b.

Monotonie

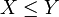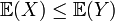Si X et Y sont des variables aléatoires tels que $X \le Y$ presque sûrement, alors $\mathbb{E}(X) \le \mathbb{E}(Y)$ .

Linéarité

L'espérance 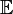$\mathbb{E}$ est un opérateur linéaire dans la mesure où

$\mathbb{E}(1)= 1,$

$\mathbb{E}(X + Y)= \mathbb{E}(X) + \mathbb{E}(Y)\,$

$\mathbb{E}(aX)= a \mathbb{E}(X)\,$

En combinant les résultats précédents, on peut obtenir :

$\mathbb{E}(aX + b)= a \mathbb{E}(X) + b\,$

$\mathbb{E}(a X + b Y) = a \mathbb{E}(X) + b \mathbb{E}(Y)\,$

pour deux variables aléatoires quelconques $X$ et $Y$ (qui doivent être définies sur le même espace probabiliste) et pour deux nombres réels $a$ et $b$ .

Loi de l'espérance itérée

Pour une variable aléatoire discrète: Pour deux variables aléatoires $X, Y$ , on peut définir l'espérance conditionnelle

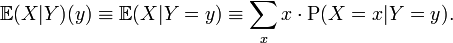
Définition — $\mathbb{E}(X|Y)(y) \equiv \mathbb{E}(X|Y=y) \equiv \sum\limits_x x \cdot \operatorname{P}(X=x|Y=y).$

qui signifie que 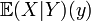$\mathbb{E}(X|Y)(y)$ est une fonction de y (en fait une variable aléatoire). L'espérance itérée vérifie

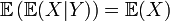Propriété — $\mathbb{E} \left( \mathbb{E}(X|Y) \right)=\mathbb{E}(X)$

Démonstration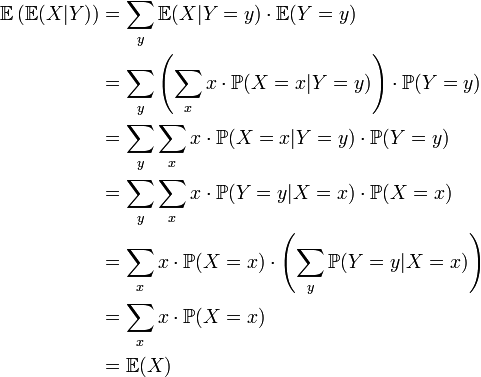

$\begin{align} \mathbb{E} \left(\mathbb{E}(X|Y) \right) &= \sum\limits_y \mathbb{E}(X|Y=y) \cdot \mathbb{E}(Y=y)\\ &=\sum\limits_y \left( \sum\limits_x x \cdot \mathbb{P}(X=x|Y=y) \right) \cdot \mathbb{P}(Y=y)\\ &=\sum\limits_y \sum\limits_x x \cdot \mathbb{P}(X=x|Y=y) \cdot \mathbb{P}(Y=y)\\ &=\sum\limits_y \sum\limits_x x \cdot \mathbb{P}(Y=y|X=x) \cdot \mathbb{P}(X=x) \\ &=\sum\limits_x x \cdot \mathbb{P}(X=x) \cdot \left( \sum\limits_y \mathbb{P}(Y=y|X=x) \right) \\ &=\sum\limits_x x \cdot \mathbb{P}(X=x)\\ &=\mathbb{E}(X) \end{align}$

Pour une variable continue: dans le cas continu, les résultats sont analogues. Dans ce cas-ci, on utilise la densité de probabilité et les intégrales à la place de la distribution et des sommes. En tout cas, le résultat reste valable:

$\mathbb{E}(X) = \mathbb{E} \left( \mathbb{E}(X|Y) \right).$

Espérance et produit

En général, l'opérateur espérance ne respecte pas le produit, c'est-à-dire que 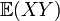$\mathbb{E}(X Y)$ est non nécessairement égal à 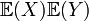$\mathbb{E}(X) \mathbb{E}(Y)$ . L'égalité est vraie cependant dès que les variables X et Y sont indépendantes. L'absence de la multiplicativité amène à étudier les Covariance et corrélation.

Espérance d'une fonctionnelle

En général, l'opérateur espérance ne respecte pas les fonctions de variable aléatoire, c'est-à-dire qu'en général:

$\mathbb{E}(g(X)) = \int_{\Omega} g(X)\, \mathbb{d}P \neq g(\mathbb{E}(X)),$

Un inégalité célèbre à ce propos est l'Inégalité de Jensen pour des fonctions convexes (ou concaves).

Estimation

On utilise souvent comme estimateur de l'espérance la moyenne empirique, qui est un estimateur:

Sans biais
Convergent selon la loi des grands nombres et même fortement convergent selon la loi forte des grands nombres
Distribué normalement asymptotiquement selon le théorème central limite

Caractère central

On considère fréquemment l'espérance comme le centre de la variable aléatoire, c'est-à-dire la valeur autour de laquelle se dispersent les autres valeurs.
En particulier, si X et 2a - X ont même loi de probabilité, c'est-à-dire si la loi de probabilité est symétrique par rapport à a, alors E(X) = a.

Mais ce point de vue n'est plus valable lorsque la loi est dissymétrique. Pour s'en persuader il suffit d'étudier le cas d'une loi géométrique, une loi particulièrement dissymétrique. Si X représente le nombre de lancers nécessaires pour obtenir le chiffre 1 avec un dé cubique, on démontre que E(X) = 6 ce qui veut dire qu'il faut en moyenne 6 lancers pour obtenir le chiffre 1. Pourtant, la probabilité que 5 essais ou moins suffisent vaut près de 0,6 et la probabilité que 7 lancers ou plus soient nécessaires est de 0,33. Les valeurs de X ne se répartissent donc pas équitablement de part et d'autre de l'espérance.

Généralisation: espérance d'une fonction d'une variable aléatoire réelle

$X$ étant une variable aléatoire réelle, une fonction $f$ supposée régulière définit une nouvelle variable aléatoire 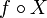$f\circ X$ notée $f (X)$ dont l'espérance, lorsqu'elle existe, s'écrit en remplaçant $k$ par $f (k)$ ou $x$ par $f (x)$ dans les formules précédentes (théorème de transfert).

Variable aléatoire discrète: $\mathbb E[f(X)] = \sum_{k=-\infty}^{+\infty} f(k)\ \mathbb P_X(k)$

Variable aléatoire continue: $\mathbb E[f(X)] = \int_{-\infty}^{+\infty} f(x)\ p_X(x)\ dx$

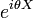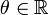En particulier, il est intéressant de considérer la variable aléatoire à valeurs complexes $e^{i \theta X}\,$ (où $\theta \in \mathbb{R}$ ) dont l'espérance mathématique est [la valeur en $θ$ de] la transformée de Fourier inverse de la densité de probabilité :

$\phi_X(\theta) = \mathbb E\left[e^{i \theta X}\right]\,$

Il s'agit de la Fonction caractéristique d'une variable aléatoire. L'exponentielle se développe en série : $\phi_X(\theta) = \mathbb E\left[\sum_{k=0}^\infty {(i \theta X)^k \over {k !}}\right]$

ou, si la densité de probabilité est une fonction suffisamment régulière :

$\phi_X(\theta) = \sum_{k=0}^\infty {(i \theta)^k \over {k !}} \mathbb E\left[X^k\right]$

Notes et références

↑ En cas de victoire, on reçoit 36 fois la mise. Le gain vaut donc ce bénéfice moins la mise initiale, c'est-à-dire qu'on aura alors réellement gagné 35 fois cette mise.

Liens externes

article sur l'espérance et exemple simple

Articles de mathématiques en rapport avec les probabilités ou les statistiques

Statistiques descriptives • Analyse des données • Visualisation des données • Estimateurs • Tests statistiques • Séries temporelles et économétrie • Statistique Mathématique • Théorie des probabilités • Variables aléatoires • Inégalités • Théorèmes limites • Processus stochastiques • La mécanique statistique • Les statistiques et l'économie • Les statistiques et la sociologie • Les statistiques et les sciences • Les probabilités et les jeux • Les équations aux dérivées partielles et les probabilités

Portail des probabilités et des statistiques
Portail de la finance

Ce document provient de « Esp%C3%A9rance math%C3%A9matique ».

Catégories : Probabilités | Mathématiques financières

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Espérance Mathématique de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Esperance mathematique — Espérance mathématique L espérance mathématique est, en probabilités, une valeur numérique permettant d évaluer le résultat moyen d une expérience aléatoire. Elle permet par exemple de mesurer le degré d équité d un jeu de hasard; elle est alors… … Wikipédia en Français
Espérance mathématique — L espérance mathématique d une variable aléatoire est l équivalent en probabilité de la moyenne d une série statistique en statistiques. Elle se note E(X) et se lit espérance de X. C est une valeur numérique permettant d évaluer le résultat moyen … Wikipédia en Français
espérance mathématique — laukiamoji vertė statusas T sritis fizika atitikmenys: angl. expectation value; expected value vok. erwartender Wert, m; Erwartungswert, m rus. математическое ожидание, n; ожидаемое значение, n pranc. espérance mathématique, f … Fizikos terminų žodynas
Espérance mathématique d'une variable aléatoire discrète X — ● Espérance mathématique d une variable aléatoire discrète X moyenne arithmétique pondérée des valeurs possibles xi de la variable X par leur probabilité pi : . (On note aussi l espérance mathématique de X, appelée parfois moyenne.) … Encyclopédie Universelle
Espérance mathématique d'une variable aléatoire continue X — ● Espérance mathématique d une variable aléatoire continue X intégrale, quand elle est absolument convergente, f (t) désignant la densité de probabilité de la variable aléatoire X … Encyclopédie Universelle
Espérance de gain — Espérance mathématique L espérance mathématique est, en probabilités, une valeur numérique permettant d évaluer le résultat moyen d une expérience aléatoire. Elle permet par exemple de mesurer le degré d équité d un jeu de hasard; elle est alors… … Wikipédia en Français
espérance — [ ɛsperɑ̃s ] n. f. • 1120; de espérer 1 ♦ L espérance : sentiment qui fait entrevoir comme probable la réalisation de ce que l on désire. ⇒ assurance, certitude, confiance, conviction, croyance, espoir. Être plein d espérance. Le vert, couleur de … Encyclopédie Universelle
Esperance de gain au poker — Espérance de gain au poker Cet article détaille les relations mathématiques entre niveau de mise et espérance de gain, dans le cas du Poker. Sommaire 1 Espérance mathématique 1.1 Loi des grands nombres 1.2 Jeu psychologique et jeu mathématique … Wikipédia en Français
Espérance De Gain Au Poker — Cet article détaille les relations mathématiques entre niveau de mise et espérance de gain, dans le cas du Poker. Sommaire 1 Espérance mathématique 1.1 Loi des grands nombres 1.2 Jeu psychologique et jeu mathématique … Wikipédia en Français
mathématique — [ matematik ] adj. et n. f. • 1265; lat. mathematicus, gr. mathêmatikos « scientifique », de mathêma « science » I ♦ Adj. 1 ♦ Relatif aux mathématiques, à la mathématique (cf. ci dessous, II); qui utilise les mathématiques, s exprime par elles.… … Encyclopédie Universelle