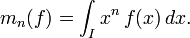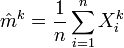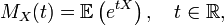Moment (mathematiques)

Moment (mathématiques)

Pour les articles homonymes, voir Moment.

En probabilités (mathématiques, statistiques), on définit le moment d'ordre n>0 d'une variable aléatoire X, s'il existe, le nombre $m_n = \mathbb{E}[~X^n~] \,$ .

Sommaire

1 Notion de moment
2 Estimation des moments
3 Moments centrés
4 Moments remarquables
5 Formules de détermination récursive des moments
6 Fonction génératrice des moments
7 Problème des moments

Notion de moment

La notion de moment en mathématiques, notamment en calcul des probabilités, a pour origine la notion de moment en physique.

Soit une fonction 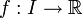$f : I \to \R$ continue sur un intervalle $I$ (non réduit à un point) de $\R$ . Étant donné un entier naturel n, le n-ième moment de $f$ est défini (sous réserve d'existence) par :

$m_n(f)=\int_I x^n\,f(x)\,dx.$

Remarque : pour un entier naturel n donné, l'ensemble des fonctions continues sur $I$ dont le moment d'ordre n existe est un espace vectoriel réel, et l'application 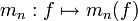$m_n : f \mapsto m_n(f)$ est une forme linéaire sur cet espace vectoriel.

Estimation des moments

Lorsque le moment existe, on utilise souvent l'estimateur suivant pour le moment d'ordre k:

$\hat m^k= \frac{1}{n}\sum_{i = 1}^{n} X^k_i\,\!$

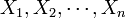à partir de l'échantillon $X_1, X_2, \cdots, X_n$ .

On peut montrer que cet estimateur est sans biais.

Moments centrés

On définit le moment centré d'ordre n>0 d'une variable aléatoire X, s'il existe, le nombre $\mu_n = \mathbb{E}[~(X-E(X))^n~] \,$ .

Moments remarquables

Certains moments sont connus sous un nom particulier. Ils sont utilisés couramment pour caractériser une variable aléatoire.

Le moment d'ordre un de la variable : $\mu = \mathbb{E}[X] \,$ correspond à l'espérance

Le moment d'ordre deux de la variable centrée : $\mu_2 = \sigma^2 = \mathbb{E} \left [\left(X-\mu\right)^2\right] \,$ correspond à la variance.

Le moment d'ordre trois de la variable centrée-réduite : $\mu_3 =\mathbb{E} \left[ \left(\frac{X-\mu}{\sigma} \right)^3 \right] \,$ correspond au coefficient d'asymétrie (skewness).

Le moment d'ordre quatre de la variable centrée-réduite : $\mu_4 =\mathbb{E}\left[\left(\frac{X-\mu}{\sigma}\right)^4\right] \,$ correspond au kurtosis.

Formules de détermination récursive des moments

En définissant

Les moments par rapport à l'origine (moments ordinaires ou raw moments en anglais):

$m_k(X) \equiv \mathbb{E}\left[X^k\right]\,$

Les moments centrés, notés généralement 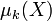$\mu_k(X)\,$ et qui se définissent ainsi :

$\mu_k(X) \equiv \mathbb{E}[(X-\mathbb{E}[X])^k]\,$

Il existe des formules (qui ressemblent à celle du binôme) permettant de calculer un moment centré d'ordre k à partir des moments ordinaires d'ordre inférieur ou égal à k, et réciproquement ; voici quelques exemples (jusqu'à l'ordre 4) :

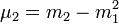
$\mu_2 = m_2 - m^2_1\,$

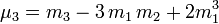
$\mu_3 = m_3 -3\,m_1\,m_2 + 2m^3_1\,$

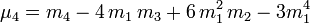
$\mu_4 = m_4 -4\,m_1\,m_3 + 6\,m^2_1\,m_2 - 3m^4_1\,\!$

et :

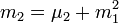
$m_2 = \mu_2 + m^2_1\,$

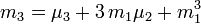
$m_3 = \mu_3 + 3\,m_1\mu_2 + m^3_1\,$

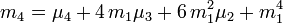
$m_4 = \mu_4 + 4\,m_1\mu_3 + 6\,m^2_1\mu_2 + m^4_1\,$

Fonction génératrice des moments

Article détaillé : Fonction génératrice des moments.

La fonction génératrice des moments d'une variable aléatoire $X$ , définie par

$M_X(t) = \mathbb{E}\left(e^{tX}\right), \quad t \in \mathbb{R},$

est utilisée afin de générer les moments associés à la distribution de probabilités de la variable aléatoire $X$ .

Problème des moments

On peut se demander si une fonction continue 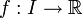$f : I \to \R$ dont tous les moments existent est déterminée par la suite de ses moments. Cette question est appelée problème des moments.

En d'autres termes : soient deux fonctions continues 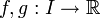$f, g : I \to \R$ dont chacune admet, pour tout entier naturel n, un moment d'ordre n. Si, pour tout 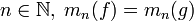$n \in \mathbb{N},\; m_n(f)= m_n(g)$ , peut-on affirmer que $f = g$ ?

D'après un théorème de Hausdorff, la réponse est affirmative lorsque $I$ est un segment $[a,\, b]$ (c'est-à-dire lorsqu'il est fermé et borné).

Démonstration

La fonction $h = f - g$ est continue sur $I$ , et tous ses moments sont nuls, car pour tout $n$ , $m n (h) = m n (f) - m n (g)$ .
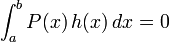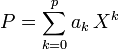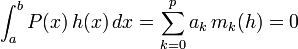On en déduit, par linéarité de l'intégrale, que $\int_a^b P(x)\,h(x)\,dx = 0$ quel que soit le polynôme réel $P$ ; en effet, si $P = \sum_{k = 0}^p a_k\, X^k$ , alors $\int_a^b P(x)\,h(x)\,dx = \sum_{k = 0}^p a_k\, m_k(h) = 0$ .
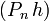Or, d'après un théorème de Weierstrass, pour toute fonction continue $[a,\, b] \to \R$ , il existe une suite de polynômes (réels) convergeant uniformément sur $[a,\, b]$ vers cette fonction. Il existe donc une suite $(P n)$ de polynômes qui converge uniformément vers $h$ sur $[a,\, b]$ . Alors, la suite des produits $(P_n\, h)$ converge uniformément vers $h 2$ sur $[a,\, b]$ et il en résulte que $\int_a^b [h(x)]^2\,dx = \lim_{n \to +\infty} \int_a^b P_n(x)\,h(x)\,dx = 0$ .
Comme $h$ est continue sur le segment $[a,\, b]$ , ceci prouve que $h = 0$ , c'est-à-dire $f = g$ .

Dans le cas général, la réponse est négative. Voici un contre-exemple probabiliste donné par William Feller. On considère la fonction $f :\, ]0,\, +\infty[\, \to \R^+$ définie par 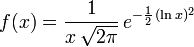$f(x) = \frac{1}{x\, \sqrt{2 \pi}}\, e^{-\frac{1}{2}\, (\ln x)^2}$ (densité de la loi log-normale), dont tous les moments existent.

On démontre (par changement de variable) que pour tout entier naturel

n

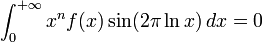, $\int_0^{+\infty} x^n f(x) \sin(2 \pi \ln x)\, dx = 0$ .

Pour tout 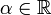$\alpha \in \R$ , on définit $g_\alpha :\, ]0,\, +\infty[\, \to \R$ par $g_\alpha(x) = f(x)\, [1 + \alpha \sin(2 \pi \ln x)]$ .

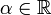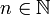Alors : quels que soient $\alpha \in \R$ et $n \in \mathbb{N}$ ,

m n (g α) = m n (f)

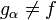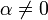, bien que $g_\alpha \neq f$ dès que $\alpha \neq 0$ .

Nota : pour tout 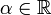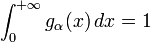$\alpha \in \R$ , $\int_0^{+\infty} g_\alpha(x)\, dx = 1$ car

m 0 (g α) = m 0 (f)

. Or, si on prend $\alpha \in [-1,\, +1]$ ,

g α

est à valeurs positives : dans ce cas,

g α

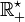est une densité de probabilité portée par $\R^\star_+\,$ , distincte de

f

si 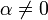$\alpha \neq 0$ , dont tous les moments existent et sont les mêmes que ceux de

f

. Ceci prouve que la loi log-normale n'est pas déterminée par ses moments.

Portail des probabilités et des statistiques

Ce document provient de « Moment (math%C3%A9matiques) ».

Catégories : Analyse réelle | Probabilités | Statistique descriptive

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Moment (mathematiques) de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Moment (mathématiques) — Pour les articles homonymes, voir Moment. En probabilités (mathématiques, statistiques), on définit le moment d ordre n>0 d une variable aléatoire X, s il existe, le nombre . Sommaire 1 … Wikipédia en Français
Moment — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Moment », sur le Wiktionnaire (dictionnaire universel) Sommaire … Wikipédia en Français
MATHÉMATIQUES (DIDACTIQUE DES) — Les problèmes posés par l’enseignement des mathématiques ne sont pas nouveaux. Au début du siècle, Henri Lebesgue était préoccupé par les conditions de l’enseignement et de la formation des professeurs. Des efforts plus récents se sont déployés… … Encyclopédie Universelle
MATHÉMATIQUES (FONDEMENTS DES) — Au sens premier et fort, le mot «fondement» désigne la base, jugée inébranlable, sur laquelle repose un corps d’énoncés, un système de connaissances, un complexe de croyances ou de conduites. «Reposer sur la base» signifie ici «trouver en elle à… … Encyclopédie Universelle
Moment Multipolaire — Les moments multipolaires sont les coefficients d un développement en série d un potentiel, utilisant de manière habituelle des puissance (ou des puissances inverses) de la distance à l origine, ainsi que de la dépendance angulaire. En principe,… … Wikipédia en Français
MATHÉMATIQUES (ENSEIGNEMENT DES) — Les problèmes que pose tout enseignement sont extrêmement complexes; ils sont liés à l’état de la société, à sa structure, à son développement économique et technique et à l’idée qu’elle se fait de son avenir. Les aborder dans leur totalité et… … Encyclopédie Universelle
Moment multipolaire — Les moments multipolaires sont les coefficients d un développement en série d un potentiel, utilisant de manière habituelle des puissance (ou des puissances inverses) de la distance à l origine, ainsi que de la dépendance angulaire. En principe,… … Wikipédia en Français
Moment map — In mathematics, specifically in symplectic geometry, the momentum map (or moment map) is a tool associated with a Hamiltonian action of a Lie group on a symplectic manifold, used to construct conserved quantities for the action. The moment map… … Wikipedia
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Moment (mathematiques)

Moment (mathématiques)

Sommaire

Notion de moment

Estimation des moments

Moments centrés

Moments remarquables

Formules de détermination récursive des moments

Fonction génératrice des moments

Problème des moments

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Moment (mathematiques)

Moment (mathématiques)

Sommaire

Notion de moment

Estimation des moments

Moments centrés

Moments remarquables

Formules de détermination récursive des moments

Fonction génératrice des moments

Problème des moments

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link