Espace vectoriel normé de dimension finie

En mathématiques, la topologie d'un espace vectoriel de dimension finie correspond à un cas particulier d'espace vectoriel normé. Cette configuration se produit si la dimension est finie.

Elle diffère du cas général au sens où il n'existe qu'une topologie compatible avec les lois de l'espace vectoriel. De plus, toutes les normes sont équivalentes.

Une norme d'un espace vectoriel de dimension finie dispose de nombreuses propriétés. Elle confère un statut d'espace complet à l'ensemble, la boule unité fermée est un compact et plus généralement les compacts sont les fermés bornés dans un tel espace.

Ici le corps sous-jacent à l'espace est celui des réels ou des complexes. Comme tout espace vectoriel complexe de dimension n est aussi un espace vectoriel réel de dimension 2n, il suffit de démontrer les propriétés pour les nombres réels pour obtenir sans plus d'effort le résultat sur les complexes.

Motivation

La configuration topologique d'un espace vectoriel E est relativement simple si le corps dispose des bonnes propriétés et si la dimension de l'espace est finie.

Elle correspond, à de nombreux égards à celle du corps des nombres réels. Les compacts se caractérisent aisément, ce sont les fermés bornés. L'espace est complet et les applications classiques, par exemple linéaires ou multilinéaires sont continues. L'étude des fonctions de E dans un espace vectoriel topologique permet de généraliser bon nombres de résultats obtenus dans le cadre des fonctions réelles de la variable réelle, elle est la structure de prédilection de la branche des mathématiques nommée géométrie différentielle.

Pour établir ces propriétés, une topologie quelconque n'est pas utilisable. Elle doit nécessairement être compatible avec les spécificités de l'espace vectoriel. Ceci signifie que la topologie est choisie de telle manière à ce que les lois de composition de E : l'addition et la multiplication externe soient continues. Une manière simple de construire une telle topologie consiste à équiper l'espace d'une norme. Une telle structure porte le nom d'espace vectoriel normé. La dimension finie implique que, du point de vue topologique, le choix de la norme n'a guère d'importance, elles se ressemblent toutes. En terme précis, elles sont dites toutes équivalentes. Toutes ces normes disposent de la même topologie sous-jacente, et, fait remarquable, il n'existe qu'une unique topologie compatible avec la structure d'espace vectoriel.

Ces propriétés ne sont vraies que si le corps sous-jacent est bien choisi. Tel est le cas s'il est égal à celui des nombres réels ou complexes. Dans le cas général, il doit posséder trois propriétés. Il existe une valuation, analogue à la valeur absolue des réels ou du module d'un complexe. Il est complet et enfin localement compact c'est-à-dire que la boule unité fermée est compact.

De grands théorèmes concernent la topologie d'un espace vectoriel de dimension finie. Un exemple est donné par le théorème de Brouwer stipulant que toute application continue de la boule unité dans elle-même possède un point fixe.

Dans cet article E désigne un espace vectoriel de dimension finie n. Le corps sous-jacent à l'espace vectoriel E est noté K, il désigne soit R soit C le corps des nombres complexes. L'espace E est équipé d'une norme, c'est-à-dire d'une application de E dans les valeurs positives de R, l'ensemble des nombres réels ayant les trois propriétés de séparation, d'homogénéité et de sous-additivité. B désigne une base de E dont les éléments sont notés (e_i).

Compacts de Rⁿ

Compacts de l'ensemble des nombres réels

Les compacts disposent de nombreuses propriétés. Elle permettent parfois d'élucider une structure topologique. Tel est le cas ici. Dans un premier temps, il est utile de caractériser ceux d'un espace réel de dimension un, ce qui revient à étudier les compacts de l'ensemble des nombres réels. On remarque que tout segment est compact, puis que tout compact est borné, comme tout compact est fermé et que tout fermé d'un compact est un compact, on obtient la caractérisation suivante :

Compacts de Rⁿ

Il est possible de munir un produit d'espaces topologiques d'une topologie, elle est appelée topologie produit. Ainsi Rⁿ est un espace topologique. Il est possible d'équiper cet espace d'une distance issue d'une norme dont la topologie associée est celle du produit. Cette norme prend le nom de norme infinie, elle associe à un vecteur la valeur absolue de sa plus grande coordonnée.

Le théorème de Tychonov stipule que le produit de compacts est un compact. Il permet de caractériser les compacts de Rⁿ, ce sont encore les fermés bornés. Ce résultat est le cadre général du théorème de Borel-Lebesgue.^[1]

Équivalence des normes

La caractérisation des compacts de Rⁿ permet d'étudier les propriétés de toutes les normes de E. L'application linéaire qui à un vecteur de E associe ses coordonnées dans la base B transportent la norme de Rⁿ dans E. Cette norme, noté ici N correspond à la plus grande valeur absolue des coordonnées. Une définition est ici utile.

Cette propriété s’écrit :

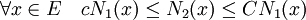
Deux normes équivalentes induisent la même topologie sur l'espace. Les propriétés purement métriques, comme la continuité uniforme ou la complétude, sont aussi équivalentes pour les deux normes. C'est-à-dire, par exemple, que si une suite de Cauchy converge pour une norme, alors elle converge pour l'autre norme.

Dans un espace de dimension finie, la situation est remarquablement simple :

En conséquence, du point de vue topologique et métrique, il n'existe qu'un unique espace vectoriel réel normé de dimension n, à un homéomorphisme uniformément continue près. Cette propriété reste vraie pour les espaces vectoriels normés complexes de dimension n, car ils sont aussi des espaces vectoriels normés réels de dimension 2n^[2]

Démonstration

• Toutes les normes d’un espace de dimension finie sont équivalentes :

Soit x_i les coordonnées de x dans la base B. Pour démontrer cette proposition, il suffit de montrer qu’une norme quelconque N₁ est équivalente à la norme particulière N(x) = max_i( | x_i | ). On a la majoration suivante :

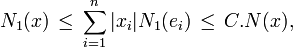
pour C égal à la somme des valeurs N₁ (e_i). Ce qui démontre la première majoration.

Pour montrer l’existence de la deuxième majoration, remarquons dans un premier temps que N₁ est une fonction continue dans l’espace vectoriel E muni de la norme N. En effet, cette application est C lipschitzienne, par l'utilisation de l'inégalité triangulaire et de l'inégalité précédente :

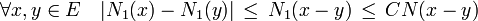
La sphère unité de E pour la norme N est homéomorphe à la sphère unité de Rⁿ pour la norme infinie, qui est compact. Elle est en effet un fermé borné de Rⁿ. L’image réciproque d’un compact par un homéomorphisme est un compact, donc la sphère unité de E pour la norme N est compact. Comme la fonction N₁ est continue, elle atteint son minimum sur cette sphère, soit c ce minimum. Il est strictement supérieur à zéro car la norme d’un vecteur non nul est non nulle. Soit x un vecteur non nul de E, alors :

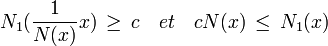
Ce qui démontre la deuxième majoration de la définition des normes équivalentes.

Conséquences

Caractérisation des compacts

Une conséquence directe de l'équivalence des normes est la caractérisation des compacts de E :

Cette proposition implique immédiatement la suivante :

Il suffit de considérer comme voisinage d’un point x de E la boule fermée de rayon un. La proposition précédente montre que ce voisinage est compact.

Cette propriété est n'est vraie que si l'espace est de dimension finie. Dans le cas contraire, la boule unité n'est pas compacte, ce résultat est connu sous le nom de théorème de Riesz.

Complétude et fermeture

Les conséquences de l'équivalence des normes sont nombreuses. En particulier, un espace normé de dimension finie possède les mêmes propriétés que l'espace Rⁿ muni de la norme produit :

Cette proposition découle simplement du fait que R est complet, le produit fini d'espaces complets est complet et donc Rⁿ est complet pour la norme produit. L'homéomorphisme entre cet espace et l'espace de même dimension permet de conclure.

Il existe un autre résultat sur la complétude, particulièrement utile pour le cas de la dimension infinie :

La métrique induite sur un sous-espace vectoriel de dimension p est homéomorphe à R^p et donc est complète. Un espace complet est un fermé donc tout sous-espace vectoriel est fermé. Un sous-espace affine est l'image par une translation d'un sous-espace vectoriel. Or la translation est un homéomorphisme car c'est une isométrie. En conséquence, tout sous-espace affine est complet donc fermé.

Démonstrations

• L'ensemble des applications linéaires d'un espace vectoriel normé dans un espace de dimension finie est complet :

Soit F un espace vectoriel normé. Soit (u_n) une suite de Cauchy d'applications linéaires de F dans E et x un vecteur de F. La suite (u_n(x)) vérifie la propriété suivante :

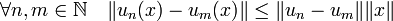
Elle est donc de Cauchy, comme E est complet elle converge. Notons u(x) cette limite. Elle définit une fonction u de F dans E. Un passage à la limite montre que u est une application linéaire vers laquelle la suite (u_n) converge, ce qui termine la démonstration.

L'ensemble des applications linéaires continues est aussi complet.

Avec les mêmes notations que celle du paragraphe précédent, il suffit de montrer que u est continue. Comme la suite (u_n) est de Cauchy, il en est de même de la suite des normes de u_n, qui est donc majorée. Soit M un tel majorant. Il vérifie :

Ce qui montre que la limite u est une application linéaire continue. La suite de Cauchy converge vers une application linéaire continue, ce qui démontre la proposition.

Continuité de quelques applications

L'application + de ExE dans E est continue si ExE est muni d'une norme quelconque (elles sont toutes équivalentes). Il en est de même pour le produit externe de RxE dans E. On en déduit une condition nécessaire et suffisante pour la continuité d'une application à valeur dans un espace de dimension finie :

Cette condition est largement utilisée pour établir la continuité, par exemple d'une fonction de R dans E. La cinématique du point offre beaucoup d'exemples de cette nature. Une telle fonction est continue si et seulement si les fonctions coordonnées dans une base quelconque sont continues.

Dans une large mesure, les applications linéaires sont continues :

Cette propriété ce généralise. Toutes les applications multilinéaires sont continues, en particulier le produit scalaire, toutes les formes bilinéaires ou quadratiques, le déterminant ou encore le produit tensoriel. En revanche, l'uniforme continuité est perdue pour les cas non linéaires.

Démonstrations

• L'application + de ExE dans E est continue :

Si ExE est équipé de la norme qui à (x, y) associe la somme des normes de x et de y, l'inégalité triangulaire montre que l'application est contractante donc continue.

• L'application . de RxE dans E est continue :

Choisissons pour la norme de RxE celle sur sup, c'est-à-dire celle qui à (λ, x) associe le maximum de la valeur absolue de λ et de la norme de x.

Soit (λ, x) et (h, k) deux points de RxE pour étudier la continuité en (λ, x). On dispose de l'égalité suivante :

Soit ε un réel strictement positif et μ le réel strictement positif défini par :

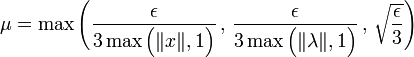
Alors :

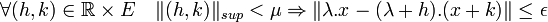
Ce qui montre la continuité de la fonction au point (λ, x). Ce point étant choisi quelconque, la continuité globale est démontrée.

• Une application linéaire a de E dans F est continue :

Soit (e_i) pour i variant de 1 à n une base de E et pour norme, celle qui à x associe la valeur absolue de sa plus grande coordonnée dans cette base. Soit k la somme des normes de a(e_i). Alors pour tout x de E différent du vecteur nul :

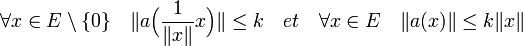
La dernière majoration montre que a est k-lipschitzienne et donc uniformément continue.

• La fonction f est continue si et seulement si la famille d'applications (f_i) pour i variant de 1 à n est constituée d'applications continues :

Soit ε_i La forme linéaire égal à un sur e_i et zéro sur tous les autres éléments de la base. La proposition précédente montre que la linéarité de ε_i montre sa continuité. la fonction f_i est la composée de la fonction f par ε_i. En conséquence, si f est continue, toutes les fonctions f_i le sont.

Réciproquement, si toutes les fonctions f_i sont continues, comme les fonctions addition et produit externe le sont aussi, f est composée d'applications continues et donc est continue, ce qui termine la démonstration.

Topologie

Unicité

Deux outils structurants ont été utilisés jusqu'à présent, une distance et une topologie conséquence directe de la donnée d'une distance. La question naturelle est celle de la nécessité d'une telle distance. Que peut-on dire d'une topologie séparée compatible avec la structure d'espace vectoriel ? Une topologie est dite compatible si l'addition et la multiplication par un scalaire sont deux applications continues. Une telle structure est qualifiée d'espace vectoriel topologique.^[3]

La réponse est identique à la précédente :

Démonstration

Ici E désigne un espace vectoriel sur K de dimension finie n. Démontrons la proposition par récurrence sur n. La technique consiste à montrer que E est homéomorphe à Kⁿ.

• Cas où n est égal à un.

Soit x un vecteur non nul de E, l'objectif est de montrer que l'application φ de K dans E, qui à k associe k.x est un homéomorphisme.

L'existence d'une telle norme ne fait pas de doute, il en existe en effet au moins une issue d'une métrique, par exemple celle issue de la norme euclidienne. Le fait que E soit de dimension un et que x soit non nul montre le caractère bijectif de φ₁. La multiplication externe sur E est continue, donc tout ouvert de E est l'image d'un ouvert de K par φ₁, car l'image réciproque d'un ouvert est un ouvert. Ainsi, à tout ouvert de E correspond un ouvert de K. La topologie de K est donc plus fine que celle de E.

Il reste à montrer que la topologie de E est plus fine que celle de K, c'est-à-dire qu'à tout ouvert de K il correspond par φ₁ un ouvert de E. Une propriété générale à tous les espaces vectoriels topologiques est utilisée ici :

Soit V un ouvert de K contenant le vecteur nul. Alors il existe un ouvert U de K contenant le vecteur nul et équilibré. C'est-à-dire que :

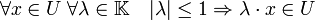
Cette propriété est démontrée dans l'article espace vectoriel topologique. Soit V un ouvert de K, l'objectif est de montrer que φ₁(V) est un ouvert. Autrement dit, si y est élément de φ₁(V) alors il existe un ouvert de K contenant y et inclus dans φ₁(V). La translation de vecteur -y est un homéomorphisme, soit U l'image de φ₁(V) par cette translation. Il suffit de montrer qu'il existe un ouvert contenant le vecteur nul et inclus dans V-y. Le fait que V-y soit un ouvert de K contenant le vecteur nul montre l'existence d'un scalaire α tel que :

Soit W un ouvert contenant le vecteur nul, mais pas x. Un tel ouvert existe car la topologie de E est séparée et W_e un ouvert équilibré, donc contenant le vecteur nul et inclus dans W. Montrons que l'ouvert αW est inclus dans V-y. Soit μx un élément de E. Si μ est plus grand que α, alors il existe un scalaire ν de module inférieur ou égal à un tel que νμx est égal à αx. Comme αx n'est pas élément de αW et que αW est équilibré, μx n'est pas élément de αW. En conclusion μx est un élément de αW seulement si μ est plus petit que α, ce qui montre que αW est inclus dans V-y et que φ₁(V) est ouvert.

• Supposons la propriété démontrée si n est égal à p et montrons là pour p + 1 :

Soit (e_i) pour i variant de 1 à p + 1 une base de E. Considérons l'application φ_p+1 de K^p+1 dans E, qui au p + 1 uplet (x_i) associe le vecteur de coordonnées (x_i) dans la base (e_i). L'application φ_p+1 est une bijection linéaire continue. L'image réciproque d'un ouvert de E est donc un ouvert de K^p+1. Une fois encore la topologie de K^p+1 apparaît plus fine que celle de E.

Il reste à montrer que la topologie de E est aussi plus fine que celle de K^p+1, ce qui revient à montrer que la réciproque de φ_p+1 est continue. Montrons dans un premier temps que l'espace vectoriel G_p engendré par e_p+1 est fermé. C'est un espace de dimension un, le paragraphe précédent montre que G_p est homéomorphe à K, soit ψ_p l'homéomorphisme, qui à x_p+1e_p+1 associe x_p+1. Si v est un point adhérent à G_p, alors il existe une suite (v_j) de G_p convergeant vers v. La suite ψ_p(v_j) est de Cauchy donc converge vers une limite ψ_p(v), ce qui montre que v est élément de G_p et donc que cet espace est fermé.

Comme l'espace vectoriel G_p est fermé, E/G_p est un espace vectoriel topologique séparé (cf Espace vectoriel topologique). Il est de dimension p et donc homéomorphe à K^p par hypothèse de récurrence. Soit χ la projection canonique de E sur E/G_p et ψ₁ l'application qui à chaque vecteur associe ses coordonnées dans la base (χ(e_i)) pour i variant de 1 à p. χ est continue par construction de la topologie quotient et ψ₁ l'est par hypothèse de récurrence. Ceci démontre que l'application de E dans K^p+1 égale à ψ₁oχ x ψ_p est continue. Il suffit alors de remarquer que cette application est la réciproque de φ_p+1 pour que la démonstration soit achevée.

Cas d'un corps valué complet

La démonstration précédente n'utilise que deux propriétés pour le corps K, la valuation qui permet d'exprimer le fait que tout ouvert contenant l'unité contient un ouvert équilibré et la complétude, qui montre que le quotient est fermé. Ainsi le théorème reste vrai pour d'autres corps comme les quaternions ou encore celui des fractions rationnelles.

L'hypothèse de la complétude est indispensable, ainsi l'extension des nombres rationnels par adjonction de la racine de deux dispose de plusieurs topologies non équivalentes, celle induite par la topologie de R ou celle induite par la norme correspondant à la racine carrée de la somme des carrés des deux coordonnées dans une base, si l'espace est considéré comme un espace vectoriel de dimension deux sur les rationnels.

Si le corps n'est pas localement compact comme pour le corps des fractions rationnelles, un des résultat précédents devient inexact. Si la topologie reste unique, la boule unité fermée n'est pas compacte.

Non équivalence en cas de dimensions différentes

Cette topologie est dépendante de la dimension. Ainsi, il n'existe pas d'homéomorphisme d'un ouvert d'un espace de dimension n dans un espace de dimension p si n et p sont différents. Pour les petites dimensions, ce résultat est intuitif. Considérons par exemple une boule ouverte d'un espace de dimension un, retirer un point détruit la connexité. Ce résultat n'est vrai qu'en dimension un. Retirer un point d'une boule ouverte d'un espace de dimension deux détruit la simple connexité, propriété qui s'avère fausse pour les dimensions supérieures.

La démonstration se fonde sur le théorème d’invariance du domaine de Brouwer, il démontre que l'image de toute application continue bijective d'un ouvert d'un espace de dimension n dans lui-même est un homéomorphisme.

Théorèmes

La topologie d'un espace vectoriel de dimension finie sur K dispose de théorèmes. Ils possèdent tous une propriété remarquable, leurs expressions sont à la fois simples et intuitives, en revanche leurs démonstrations est difficile et fait appel à un large attirail d'outils.^[4] On peut citer par exemple le théorème de la boule chevelue aux applications multiples tant dans le domaine de la fusion nucléaire pour la géométrie d'un tokamak que de la météorologie sur l'existence de système cyclonique ou anticyclonique.

En dimension deux, pour séparer l'espace en deux composantes connexes le plus simple est de dessiner une ligne qui ne se croise pas elle-même et dont le point initial et final sont confondu. On parle alors de lacet simple de Jordan. Le lacet correspond à la frontière entre les deux zones. Ce théorème se généralise, à une dimension finie quelconque. Ainsi une surface homéomorphe à celle d'une sphère divise encore l'espace en deux composantes connexes.

Ce théorème est démontré en dimension deux par Camille Jordan et il faut attendre 1912 pour qu'il soit généralisé pour toute dimension finie par Luitzen Egbertus Jan Brouwer^[5]. Il est une conséquence du théorème suivant :

Une conséquence directe est que φ est un homéomorphisme. La démonstration du théorème d'invariance encore appelé de la boule ouverte, utilise le résultat suivant :

Un autre théorème lui ressemble un peu. Il permet de montrer que dans un espace euclidien de dimension n, pour tout ensemble de n solides bornés et mesurables, il existe un hyperplan qui coupe chacun des solides en deux parties de volumes égaux. Ce résultat est connu nous le nom de théorème du sandwich au jambon et s'énonce en disant qu'il est toujours possible de couper d'un coup de couteau le sandwich ne manière à ce que le partage des deux morceaux de pain et de la tranche de jambon soit équitable.

Enfin de nombreux résultats technique permettant d'approximer une fonction, citons ici un célèbre théorème :

Théorème de Stone-Weierstrass —  Soit n un entier strictement positif, C un compact de Rⁿ et φ une application continue d'un compact C à valeurs dans R. Si ε est un réel strictement positif, il existe un polynôme P(x) qui approxime uniformément φ à ε près.

Notes et références

Notes

Liens externes

• (fr) Espaces vectoriels normés de dimension finie et équivalence des normes par les mathématiques.net
• (en) Espace vectoriel topologique de dimension finie par B. Rosenfield de l'université de Minnesota
• (fr) Espaces vectoriels topologiques Livre IV par Nicolas Bourbaki

Références

• Helmuth H. Schaefer, Topological vector spaces., Springer-Verlag, New York, 1971 (ISBN 0387987266)

• Walter Rudin, Analyse réelle et complexe : cours et exercices [détail des éditions]

• S. Lang Analyse Réelle InterEditions, Paris 1977 (ISBN 2729600595)

• N. Bourbaki Espaces vectoriels topologiques Masson 1981 (ISBN 2225684103)

• Portail des mathématiques