- Espace connexe
-
Connexité (mathématiques)
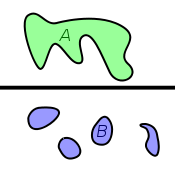
 Un archipel, comme celui des îles Canaries, n'est pas connexe : il n'est pas possible de passer à pied sec d'une île à l'autre. Les îles sont les composantes connexes de l'archipel.
Un archipel, comme celui des îles Canaries, n'est pas connexe : il n'est pas possible de passer à pied sec d'une île à l'autre. Les îles sont les composantes connexes de l'archipel.
La connexité est une notion de topologie qui formalise le concept d'« objet d'un seul tenant ». Un objet est dit connexe s'il est fait d'un seul « morceau », dans le cas contraire, chacun des morceaux est une composante connexe de l'objet étudié.
Sommaire
Définition
Soit un espace topologique E. Les trois propositions suivantes sont équivalentes :
- E n'est pas la réunion de deux ouverts non vides disjoints ;
- E n'est pas la réunion de deux fermés non vides disjoints ;
- Toute application continue de E dans un ensemble à deux éléments muni de la topologie discrète est constante.
Cette dernière caractérisation est souvent la plus commode à utiliser pour démontrer un résultat de connexité.
Dans le cas où ces conditions sont remplies on dit que l'espace E est connexe.
Une partie X d'un espace topologique E est dite connexe si elle est un espace connexe lorsqu'elle est munie de la topologie induite.
Connexité et nombres réels
- L'ensemble des nombres réels
 est connexe.
est connexe.
On montre d'abord que tout intervalle fermé borné
![[a,b]\,](/pictures/frwiki/55/7f3408c72246eece3d5542fc853ce417.png) est connexe. Soient en effet deux fermés non vides C et D formant une partition de [a,b]. Sur le compact
est connexe. Soient en effet deux fermés non vides C et D formant une partition de [a,b]. Sur le compact 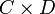 , la fonction continue
, la fonction continue 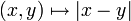 a un minimum strictement positif
a un minimum strictement positif 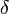 , réalisé en
, réalisé en 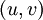 . Alors
. Alors ![w=\frac{u+v}{2}\in [a,b]\,](/pictures/frwiki/97/a2d52fa81df971ea87c28f86c13e26a0.png) . Mais
. Mais 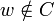 : sinon la distance de
: sinon la distance de 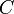 à
à 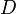 serait
serait 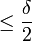 . De même,
. De même, 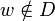 . On aboutit donc à une contradiction.
. On aboutit donc à une contradiction.Comme
![\R =\cup_{n\ge 1}[-n,n]\,](/pictures/frwiki/100/d8c6883b215e646f742051e0640f2228.png) , on en déduit que R est connexe, en tant que réunion de parties connexes dont l'intersection n'est pas vide.
, on en déduit que R est connexe, en tant que réunion de parties connexes dont l'intersection n'est pas vide.- Les parties connexes de
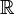 sont les intervalles. Un raisonnement analogue à celui montrant la connexité des nombres réels montre que les intervalles sont connexes. Considérons maintenant un ensemble A non vide qui ne soit pas un intervalle. il existe donc un élément a tel qu'il existe dans A au moins un élément plus petit et un élément plus grand que a. Alors
sont les intervalles. Un raisonnement analogue à celui montrant la connexité des nombres réels montre que les intervalles sont connexes. Considérons maintenant un ensemble A non vide qui ne soit pas un intervalle. il existe donc un élément a tel qu'il existe dans A au moins un élément plus petit et un élément plus grand que a. Alors ![]-\infty,a[](/pictures/frwiki/49/1c5b9412c130c8defab790b16ed84156.png) et
et ![]a,+\infty[](/pictures/frwiki/98/b945128804f9aaababab31442e9529d2.png) forment une partition en deux ouverts disjoints.
forment une partition en deux ouverts disjoints.
Par exemple
![[0,1] \cup [2,3] \,](/pictures/frwiki/52/42d5fc9b6e1f76ba5785f5e333018961.png) n'est pas connexe.
n'est pas connexe.Propriétés
Union, intersection, adhérence
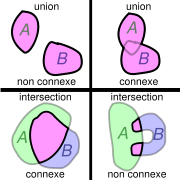
Si X et Y sont deux parties connexes d'un espace topologique E, en général l'union et l'intersection de X et Y ne sont pas connexes.
En revanche, l'union des deux parties connexes est connexe si elles ont un point commun. Plus généralement, si
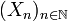 est une suite de parties connexes telle que chacune a un point commun avec la suivante :
est une suite de parties connexes telle que chacune a un point commun avec la suivante : 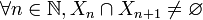 alors la réunion
alors la réunion 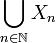 est connexe.
est connexe.Autre généralisation : la réunion d'une famille quelconque
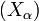 de parties connexes de E est connexe, si leur intersection est non vide. Exemple d'application : toute partie connexe par arcs est connexe.
de parties connexes de E est connexe, si leur intersection est non vide. Exemple d'application : toute partie connexe par arcs est connexe.Si
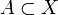 est connexe, toute partie B telle que
est connexe, toute partie B telle que 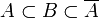 est connexe (on a désigné par
est connexe (on a désigné par 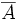 l'adhérence de A , qui dans ce cas est donc aussi connexe ).
l'adhérence de A , qui dans ce cas est donc aussi connexe ).Composantes connexes
Étant donné un point
 dans un espace topologique
dans un espace topologique  , on peut considérer la plus grande partie connexe contenant
, on peut considérer la plus grande partie connexe contenant  , qui est aussi l'union des parties connexes contenant
, qui est aussi l'union des parties connexes contenant 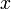 . On la note
. On la note 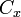 et on l'appelle composante connexe de
et on l'appelle composante connexe de  dans
dans  .
.Au minimum, on a Cx = {x} ; cela signifie que {x} est le seul sous-ensemble connexe de E contenant x mais pas forcément que x est un point isolé (cf. exemples).
Au maximum, on a Cx = E ; c'est le cas où E est connexe.
On définit une relation d'équivalence sur E de la manière suivante : on dit que x et y sont connectés si et seulement si
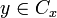 . Cette relation équivaut à
. Cette relation équivaut à 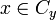 .
.Les classes d'équivalence pour cette relation sont appelées composantes connexes de E ; ainsi tout espace topologique se décompose en union disjointe de parties connexes (il n'y en a qu'une si l'espace est connexe !)
Exemples :
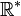 a deux composantes connexes :
a deux composantes connexes : 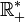 et
et 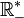 .
.- Dans
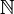 et plus généralement dans un espace muni de la topologie discrète, les composantes connexes sont les singletons.
et plus généralement dans un espace muni de la topologie discrète, les composantes connexes sont les singletons. - Dans
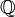 aucun point n'est isolé, mais les composantes connexes sont aussi les singletons. Le même phénomène se produit pour l'ensemble de Cantor.
aucun point n'est isolé, mais les composantes connexes sont aussi les singletons. Le même phénomène se produit pour l'ensemble de Cantor. - Le groupe
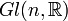 des matrices inversibles de taille n a deux composantes connexes, données par le signe du déterminant.
des matrices inversibles de taille n a deux composantes connexes, données par le signe du déterminant.
Un espace topologique dont les composantes connexes sont les singletons est dit totalement discontinu.
Connexité et continuité
On sait caractériser les espaces connexes par le fait que toute fonction continue à valeurs dans
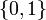 est constante.
est constante.En fait, on peut dire plus généralement que l'image d'un espace connexe par une application continue est toujours connexe. Plus précisément si
 est un espace connexe,
est un espace connexe,  un espace topologique et
un espace topologique et  une application continue, alors
une application continue, alors 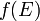 est une partie connexe de
est une partie connexe de  .
.Dans le cas où
 est
est  on obtient le théorème des valeurs intermédiaires : si
on obtient le théorème des valeurs intermédiaires : si  est un espace connexe et si une fonction continue
est un espace connexe et si une fonction continue 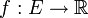 prend les valeurs a et b alors elle prend toute valeur c comprise entre
prend les valeurs a et b alors elle prend toute valeur c comprise entre 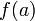 et
et 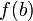 .
.Applications localement constantes
Définition
Soit X un espace topologique, et Y un espace séparé (par exemple un espace métrique).
Une application f de X dans Y est dite localement constante sur X si pour tout
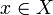 , il existe un voisinage de x sur lequel f est constante.
, il existe un voisinage de x sur lequel f est constante.Une fonction localement constante sur X n'est pas forcément constante sur X. Intuitivement, c'est le cas si l'ensemble X est « en un seul morceau », ce que montre le théorème suivant
Théorème
Si X est connexe, toute application localement constante sur X est constante.
Deux applications fondamentales à l'Analyse
Pour montrer qu'une propriété est vraie pour tous les points d'une partie que l'on sait connexe, on montre que l'ensemble des points qui la satisfait est ouvert et fermé. C'est ce qu'on fait pour le théorème d'unicité global des solutions d'une équation différentielle, et pour le principe du prolongement analytique.
Applications à la topologie
Les applications sont nombreuses. La droite
 et le plan
et le plan 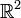 ne sont pas homéomorphes : si tel était le cas, la droite privée d'un point serait homéomorphe au plan privé d'un point. Mais le second espace est connexe, le premier ne l'est pas.
ne sont pas homéomorphes : si tel était le cas, la droite privée d'un point serait homéomorphe au plan privé d'un point. Mais le second espace est connexe, le premier ne l'est pas.Le même argument montre que le cercle S1 n'est pas homéomorphe à un intervalle.
Cet argument ne s'étend pas aux dimensions supérieures. Si on veut montrer en utilisant les mêmes idées que
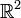 et
et 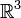 ne sont pas homéomorphes, il faut faire intervenir la connexité simple (c'est à dire la connexité par arcs de l'espace des chemins fermés). Le résultat est encore vrai pour les dimensions supérieures, mais fait appel pour la démonstration à outils plus puissant comme l'homologie.
ne sont pas homéomorphes, il faut faire intervenir la connexité simple (c'est à dire la connexité par arcs de l'espace des chemins fermés). Le résultat est encore vrai pour les dimensions supérieures, mais fait appel pour la démonstration à outils plus puissant comme l'homologie.On peut encore citer, comme application de la connexité, l'analyse de l'énigme des trois maisons. l'objet de cet énigme est de relier trois points du plan identifiés à des maisons à trois autres, identifiés à des fournisseurs (eau, gaz et électricité). Chaque maison doit être reliée aux trois fournisseurs et les liens ne doivent pas se croiser. La démonstration de l'impossibilité de résolution se fonde sur le théorème de Jordan, qui s'exprime en termes de connexité.
Voir aussi
- Portail des mathématiques
Catégorie : Topologie générale
Wikimedia Foundation. 2010.