Espace normé

Espace normé

Espace vectoriel normé

Un espace vectoriel normé est une structure mathématique qui développe des propriétés géométriques de distance compatible avec les opérations de l'algèbre linéaire. Développée notamment par David Hilbert et Stefan Banach, cette notion est très importante en analyse et plus particulièrement en analyse fonctionnelle avec l'utilisation d'espaces de Banach tels que les espaces Lp ou les espaces de Sobolev Wk, p.

Sommaire

Structure générale

Définition formelle

Article détaillé : Norme (mathématiques).

Soit K un corps muni d'une valeur absolue (par exemple le corps des réels ou des complexes).

Définition —  Un K-espace vectoriel E est dit normé E lorsqu'il est muni d'une norme, c'est-à-dire une application N de E dans les réels positifs satisfaisant les hypothèses suivantes :

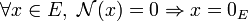  • séparation : \forall x \in E,\ \mathcal N(x)=0 \Rightarrow x=0_E  ;
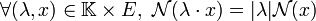  • homogénéité : \forall (\lambda, x)\in \mathbb K \times E, \ \mathcal N (\lambda \cdot x) = |\lambda| \mathcal N (x)  ;
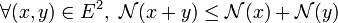  • sous-additivité : \forall (x,y) \in E^2,\ \mathcal N (x + y) \leq \mathcal N (x) + \mathcal N (y) .

S'il n'y a pas de risque d'ambiguïté, la norme d'un élément x est notée \|x\|.

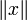La boule unité (fermée) de E est l'ensemble des vecteurs de norme inférieure ou égale à 1.

Sous-espace et espace produit

Tout sous-espace vectoriel d'un espace vectoriel normé est normé par la restriction de la norme.

Soit (E, NE) et (F, NF) deux espaces vectoriel normés, alors la norme NExF définie par l'égalité suivante, confère au produit ExF le statut d'espace vectoriel normé :

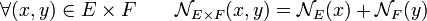
\forall (x,y) \in E\times F \qquad \mathcal N_{E\times F}(x,y) = \mathcal N_E(x) + \mathcal N_F(y)

Espace quotient

Soit F un sous-espace vectoriel de E un espace vectoriel normé. On définit l'application 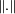\scriptstyle {\|.\|}E/F du quotient E/F par :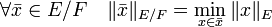

\forall \bar x \in E/F \quad \|\bar x\|_{E/F} = \min_{x\in \bar x} \|x\|_E

L'application est homogène, en effet :

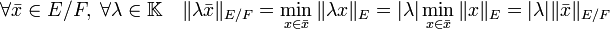
\forall \bar x \in E/F,\; \forall \lambda \in \mathbb K \quad \|\lambda \bar x\|_{E/F} = \min_{x\in \bar x}\|\lambda x\|_E = |\lambda | \min_{x\in \bar x} \|x\|_E=|\lambda |\|\bar x\|_{E/F}

Elle est de plus sous-additive, en effet :

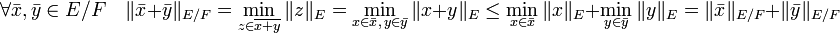
\forall \bar x, \bar y \in E/F \quad \|\bar x+\bar y\|_{E/F} = \min_{z\in \overline {x+y}}\|z\|_E = \min_{x\in \bar x,\, y \in \bar y} \|x + y\|_E \le \min_{x\in \bar x} \|x\|_E + \min_{y\in \bar y} \|y\|_E = \|\bar x\|_{E/F}+\|\bar y\|_{E/F}

Par défaut, l'espace vectoriel quotient est donc équipé d'une semi-norme. Si F n'est pas fermé, alors tout point adhérent à F est manifestement de semi-norme nulle dans l'espace quotient. En revanche, si F est fermé, la propriété de séparation est vérifiée. En effet, si F est fermé et si x n'est pas élément de F, alors il existe un scalaire ε strictement supérieur à zéro tel que tout point de F est à une distance supérieure à ε de x. Ce qui montre que la norme de la classe de x est au moins égale à ε, donc l'application 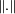\scriptstyle {\|.\|}E/F vérifie la propriété de séparation.

Propriété —  Le quotient E/F munis de l'application 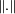\scriptstyle {\|.\|}E/F est un espace vectoriel normé si et seulement si F est fermé. Dans le cas contraire, l'application 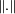\scriptstyle {\|.\|}E/F est une semi-norme.

Exemples fondamentaux

Soit X un espace mesuré.
L'espace Lp(X) des fonctions p-intégrables sur X presque partout définies à valeurs réelles ou complexes, muni de la norme p associée, ainsi que l'espace L∞(X) des fonctions presque partout définies et bornées sur X à valeurs réelles ou complexe, muni de la borne supérieure essentielle du module, sont des espaces vectoriels normés.

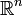  • Si X est un segment de \R ou plus généralement un compact de \R^n, muni de la mesure de Lebesgue, ces espaces induisent les normes usuelles sur les espaces de fonctions continues sur X ;
  • si X est un ensemble fini 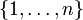\left\{1, \dots, n\right\} muni de la mesure de comptage, on retrouve les normes usuelles sur Kn ;
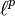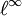  • si X est l'ensemble des entiers naturels muni de la mesure de comptage, on obtient les espaces de suites p-sommables \ell^p et l'espace des suites bornées \ell^{\infty}.

Explicitement, 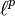\ell^p est l'ensemble des suites 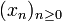(x_n)_{n\ge 0} de nombres complexes, muni de la norme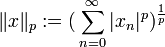

\Vert x\Vert_p:=\big(\sum_{n=0}^\infty \vert x_n\vert^p\big)^{\frac{1}{p}}

Remarque. Dans ces exemples, il n'est pas trop difficile de vérifier que la norme 1 ou 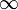\infty est bien une norme. Pour la norme 2, c'est une conséquence de l'inégalité de Cauchy-Schwarz. Pour p quelconque, l'inégalité triangulaire, qui porte le nom d'inégalité de Minkowski, est plus cachée.

Topologie

Equivalence des topologies

Comme le montre l'article norme, il existe une topologie induite par la norme et pour lequel l'addition et la multiplication externe sont continues.

Un sous-espace vectoriel F hérite donc de deux topologies, celle issue de sa norme (restriction de la norme sur l'espace entier) et celle induite par celle de l'espace vectoriel. Elles sont confondues, en effet, elles possèdent toutes les deux comme base de voisinages d'un point x de F l'intersection des boules ouvertes de centre x avec F. Or deux topologies ayant pour chaque point une même base de voisinages, sont confondus.

La configuration est la même pour le produit de deux espaces E1 et E2. Si x (resp. y) est un point de E1 (resp. E2), alors le produit des boules ouvertes de centres x et y forment une base de voisinages pour les deux topologies.

Elle reste analogue pour un quotient d'espace E/F. Montrons tout d'abord que la topologie induite par la norme est plus fine que celle issue de la topologie quotient. Soit φ est la projection canonique de E dans E/F , cette application est 1-Lipschitzienne elle est donc continue. Tout ouvert de E/F issue de la norme quotient admet donc un ensemble antécédent ouvert et par définition est un ouvert pour la topologie quotient.

Montrons ensuite que la topologie issue du quotient est plus fine que celle induite par la norme. Soit Ω un ouvert de E/F pour la topologie quotient contenant un point φ(x). Il est image d'un ouvert O par φ, par définition de la topologie quotient. L'image réciproque de Ω par φ est le cylindre O + F. Le point x de E est élément du cylindre, et comme O est ouvert, le cylindre l'est aussi. Il existe donc une boule ouverte B non vide de centre x dans le cylindre. Soit r son rayon. La borne supérieure de la distance entre un point de la boule de centre le vecteur nul et de rayon r et F est non nul (sinon F est égal à E et le quotient ne comporte qu'un point, les deux topologies sont alors trivialement confondues) et majoré par r (car le vecteur nul est élément de F). Soit S cette borne supérieure. Alors la boule de centre φ(x) et de rayon S est incluse dans Ω. Ceci montre que Ω est un ouvert pour la topologie induite par la norme et termine la démonstration.

Ainsi, les topologies induites par un sous-espace, un produit d'espaces ou un quotient sont confondues avec les topologies issues des normes.

Opérateur borné

Un opérateur borné est une application linéaire par laquelle l'image de la boule unité est incluse dans une boule de l'espace but.

L'ensemble des opérateurs bornés entre deux K-espaces vectoriels normés E et F se note parfois Lborné(E, F). C'est un sous-espace vectoriel de L(E, F) normé par la norme d'opérateur. Lorsque ces espaces vectoriels normés sont réels ou complexes, l'espace des opérateurs bornés s'identifie avec l'espace Lc(E,F) des applications linéaires continues.

Complétude

Article détaillé : Espace complet.

Un espace vectoriel normé n'est pas nécessairement complet, c'est à dire que les suites de Cauchy ne sont pas nécessairement convergentes. Tel est le cas, par exemple pour l'espace préhilbertien engendré par les polynômes trigonométriques. De manière plus générale :

proposition 1 —  Un espace vectoriel normé n'est jamais complet s'il admet une base infinie dénombrable.

En revanche, il existe un bon complété pour un espace vectoriel normé E :

proposition 2 —  Il existe un espace vectoriel normé complet F et une application linéaire injective J de E dans F tel que J est une isométrie de E dans F et l'image de J est dense dans F.

En général, J(E) est identifié à F. Ainsi, E apparait comme un sous-espace vectoriel de F, la norme sur E induite par la norme de F coïncide avec celle initiale car J est une isométrie. Un espace vectoriel normé complet porte le nom d'espace de Banach.

Si le corps n'est pas complet, l'espace F n'est plus de même nature. Ainsi un espace vectoriel de dimension un sur le corps des rationnels est isomorphe à l'espace vectoriel des nombres réels sur le corps des rationnels.

La complétude de F se transmet à celle de l'espace des applications linéaires dans K.

Proposition 3 —  Soit E et F deux espaces vectoriel sur un corps K. Si F est complet alors Lc(E, F) muni de la norme des opérateurs est un espace complet.

La complétude Ec d'un espace E de modifie pas la nature de l'espace des applications linéaires de E dans F si F est complet :

Proposition 4 —  Soit E un espace vectoriel de complété Ec et F un espace vectoriel complet. Alors, pour la norme des opérateurs, il existe un isomorphisme isométrique entre Lc(E, F) et Lc(Ec, F).


Démonstrations
  • Un espace vectoriel normé n'est pas complet s'il admet une base dénombrable :

Soit (en), où n est un entier strictement positif, une base de E. Quitte à effectuer une homothétie sur chaque vecteur, il est possible de choisir la norme de en égal à 1/n2. Considérons la série de terme générale en :

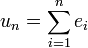
u_n = \sum_{i=1}^n e_i

La suite associée est bien de Cauchy :

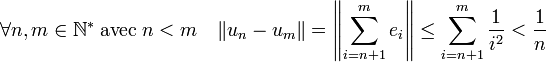
\forall n,m \in \mathbb N^* \; \text{avec}\; n < m \quad \|u_n -u_m\| = \left\|\sum_{i=n+1}^m e_i\right\| \le \sum_{i=n+1}^m \frac 1{i^2}<\frac 1n

Si cette suite convergeait vers une limite l, l'expression dans la base (en) serait :

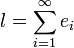
l = \sum_{i=1}^{\infty} e_i

Cette limite n'existe pas car l'expression dans la base d'un vecteur contient au plus un nombre fini de coefficients non nuls, ce qui n'est pas le cas ici.

  • Il existe un espace vectoriel normé complet F et une application linéaire injective J de E dans F tel que J est une isométrie de E dans F et l'image de J est dense dans F.

La démonstration se construit en plusieurs étapes :

Construction de F :

E est un espace métrique, il admet donc un complété F. C'est à dire qu'il existe une isométrie injective J de E dans F. Une esquisse de démonstration est donnée dans l'article détaillé. L'espace E est maintenant identifié à son image par J.

Il est nécessaire de munir F d'une structure d'espace vectoriel.

Prolongement de l'addition de E dans F :

L'addition est une application uniformément continue de ExE sur F (cf article Norme (mathématiques)). Elle se prolonge en une application continue de l'adhérence de l'ensemble de départ dans F car F est complet (cf l'article Continuité uniforme).

L'élément neutre de E est celui de F. En effet, soit x un élément de F, (xn) une suite de E convergeant vers x, alors la suite (0 + xn) converge aussi vers x.

Soit x un élément de F et (xn) une suite de E convergeant vers x. Soit notons y la limite de la suite (-xn) qui est manifestement de Cauchy. Comme la suite (xn - xn) est constante égale au vecteur nul, elle converge. La continuité de l'addition montre que y est l'inverse de x, ce qui montre que tout élément est inversible.

Soit x, (resp. y), (resp. z) un élément de F et (xn) (resp. (yn)), (resp. (zn)) une suite convergeant vers x, (resp. y), (resp. z). Les deux suites (xn + yn) + zn et xn + (yn + zn) sont égales car l'addition dans E est associative et de Cauchy car la somme de suites de Cauchy est de Cauchy. En conséquence, elle converge vers la même limite. Ceci démontre que l'addition dans F est associative.

La commutativité se démontre de manière analogue.

Prolongement de la multiplication externe de KxE dans F :

Soit M un réel strictement positif, sur la boule de rayon M, la multiplication externe est uniformément continue (cf l'article Norme (mathématiques)). Il est donc possible de prolonger la multiplication sur la boule de rayon M par continuité. Comme le prolongement par continuité est unique, il ne dépend pas de la valeur de M. Et comme tout scalaire et tout vecteur est inclus dans une boule, ce prolongement s'étend à tout scalaire et à tout vecteur de F.

Une approche analogue à l'addition montre que les axiomes définissant la multiplication externe d'un espace vectoriel sont tous vérifiés.

  • Soit E et F deux espaces vectoriel sur un corps K. Si F est complet alors Lc(E, F) muni de la norme des opérateurs est un espace complet.

Soit (un) une suite de Cauchy d'applications linéaires continues de E dans F et x un vecteur de E. La suite (un(x)) vérifie la propriété suivante :

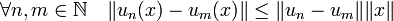
\forall n,m \in \mathbb N \quad \|u_n(x) - u_m(x)\| \le \|u_n-u_m \| \|x\|
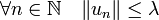Elle est donc de Cauchy, comme E est complet elle converge. Notons u(x) cette limite. Elle définit une fonction u de E dans F. Un passage à la limite montre que u est une application linéaire vers lequel la suite (un) converge simplement ; de plus, comme (un) est une suite de Cauchy, elle est bornée par un certain λ, d'où \forall n \in \mathbb N \quad \|u_n\| \le \lambda et donc par passage à la limite sur n, on obtient 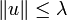\|u\| \le \lambda, ce qui montre la continuité de u. On montre enfin que (un) converge en u dans Lc(E, F) : pour ε > 0, il existe n0 dans 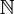\mathbb N tel que
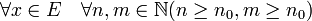
\forall x \in E \quad \forall n,m \in \mathbb N (n \geq n_0, m \geq n_0)
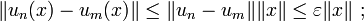
\|u_n(x) - u_m(x)\| \le \|u_n-u_m \| \|x\| \le \varepsilon \|x\| \text{ ;}
en passant à la limite sur m, on déduit
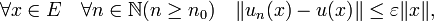
\forall x \in E \quad \forall n \in \mathbb N (n \geq n_0) \quad \|u_n(x) - u(x)\| \le \varepsilon \|x\| \text{,}
d'où
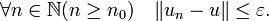
\forall n \in \mathbb N (n \geq n_0) \quad \|u_n - u\| \le \varepsilon \text{.}
Ceci achève la démonstration.

Théorème de Riesz

Article détaillé : Théorème de Riesz.

Ce théorème stipule que si la boule unité (fermée) d'un espace vectoriel réel ou complexe normé E est compacte, alors E est de dimension finie.

Autrement dit, la boule unité fermée d'un espace vectoriel normé de dimension infinie est toujours non compacte.
Cependant, la boule unité fermée de son dual topologique (de dimension infinie également) est faiblement compacte, c'est-à-dire compacte pour la topologie faible.

Cas particuliers

Espace préhilbertien

Article détaillé : Espace préhilbertien.

Un espace est dit préhilbertien s'il dispose d'une norme dérivée d'un produit scalaire. Ce type d'espace se caractérise par le fait qu'il est isométriquement isomorphe à un espace dense de son dual. Une propriété est manquante pour établir de nombreux théorèmes démontrables à l'aide du produit scalaire, la complétude. Il est possible de compléter un préhilbertien, soit à l'aide de la méthode explicité dans cet article soit en remarquant que le complété est isomorphe au dual.

Il existe une autre manière de caractériser un tel espace. Toute norme vérifiant l'identité du parallélogramme dérive d'un produit scalaire. Cette propriété est démontré dans l'article Espace euclidien pour le cas réel et étendu dans le cas complexe dans l'article Espace hermitien.

Dimension finie

Article détaillé : Topologie d'un espace vectoriel de dimension finie.

Soit E un espace vectoriel de dimension finie sur \R, sur \mathbb{C} ou sur un corps valué complet localement compact.

  • Il n'existe qu'une seule topologie sur E qui en fasse un espace vectoriel topologique séparé. En outre, l'espace E muni de cette topologie est normable.
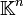  • Pour cette topologie, E est (uniformément) homéomorphe à \mathbb{K}^n.
  • En particulier, toutes les normes sur E sont équivalentes.
  • L'espace E est complet, c'est donc un espace de Banach.
  • Les parties compactes de E sont les fermés bornés.
  • La boule unité fermée de E est compacte.
  • Toute application linéaire de E dans un espace vectoriel normé quelconque est continue.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Espace vectoriel norm%C3%A9 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Espace normé de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • espace normé — normuotoji erdvė statusas T sritis fizika atitikmenys: angl. normalized space; normed space vok. normierter Raum, m rus. нормированное пространство, n pranc. espace normé, m …   Fizikos terminų žodynas

  • Norme d'operateur — Norme d opérateur En mathématiques, une norme d opérateur ou norme subordonnée est une norme définie sur l espace des opérateurs bornés, ie des opérateurs continus, entre deux espaces vectoriels normés. Soient E et F deux espaces vectoriels… …   Wikipédia en Français

  • Norme subordonnée — Norme d opérateur En mathématiques, une norme d opérateur ou norme subordonnée est une norme définie sur l espace des opérateurs bornés, ie des opérateurs continus, entre deux espaces vectoriels normés. Soient E et F deux espaces vectoriels… …   Wikipédia en Français

  • Espace vectoriel normé de dimension finie — Topologie d un espace vectoriel de dimension finie En mathématiques, la topologie d un espace vectoriel de dimension finie correspond à un cas particulier d espace vectoriel normé. Cette configuration se produit si la dimension est finie. Elle… …   Wikipédia en Français

  • Norme d'opérateur — En mathématiques, et plus particulièrement en analyse fonctionnelle, une norme d opérateur ou norme subordonnée est une norme définie sur l espace des opérateurs bornés entre deux espaces vectoriels normés. Entre deux tels espaces, les opérateurs …   Wikipédia en Français

  • Espace strictement convexe — En mathématiques, un espace strictement convexe est un espace normé dont la boule unité est strictement convexe dans le sens précisé ci dessous. Cette propriété de la norme est moins forte que celle possédée par la norme d un espace uniformément… …   Wikipédia en Français

  • Espace Préhilbertien — En mathématiques, un espace préhilbertien est défini comme un espace vectoriel réel ou complexe muni d un produit scalaire. Cette notion généralise celles d espace euclidien ou hermitien, en omettant l hypothèse de la dimension finie. Le cas… …   Wikipédia en Français

  • Espace Vectoriel Normé — Un espace vectoriel normé est une structure mathématique qui développe des propriétés géométriques de distance compatible avec les opérations de l algèbre linéaire. Développée notamment par David Hilbert et Stefan Banach, cette notion est très… …   Wikipédia en Français

  • Espace prehilbertien — Espace préhilbertien En mathématiques, un espace préhilbertien est défini comme un espace vectoriel réel ou complexe muni d un produit scalaire. Cette notion généralise celles d espace euclidien ou hermitien, en omettant l hypothèse de la… …   Wikipédia en Français

  • Espace vectoriel norme — Espace vectoriel normé Un espace vectoriel normé est une structure mathématique qui développe des propriétés géométriques de distance compatible avec les opérations de l algèbre linéaire. Développée notamment par David Hilbert et Stefan Banach,… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”