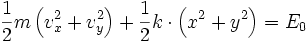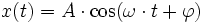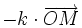Ellipse de hooke

L'ellipse de Hooke est la trajectoire d'un mobile élastiquement lié à un point fixe.

Historique

Robert Hooke (1635-1703) énonça sa « loi de Hooke » sur les ressorts en 1670 :

F = -k·Δl

F étant la force exercée par le ressort, Δl son allongement et k la constante de raideur. Il comprit que dans le cas du pendule sphérique (une petite masse pesante attachée par une ficelle de longueur l fixée en un point O), si l'on considérait seulement les petites oscillations, la force de rappel vers la position d'équilibre stable (la verticale descendante), composée du poids et de la tension du fil, s'écrivait

,

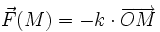avec k = m·(g/l), g étant l'accélération de la gravité.

Le théorème de l'énergie cinétique^[1] de Torricelli se muait dans ce cas en :

(l'énergie cinétique 1/2·m·v² varie à l'inverse de l'énergie potentielle élastique 1/2·k·OM²), où

• x et y sont les coordonnées cartésiennes du mobile M par rapport au point d'attache O ;
• v_x et v_y sont les composante du vecteur vitesse.

Cette équation différentielle de Newton, comme nous disons de nos jours, avait déjà été résolue le cas à une dimension (mouvement linéaire) par Huygens dans son Horologium ; Huygens avait trouvé intuitivement la solution :

trouvant ainsi la formule du pendule simple de Galilée :

.

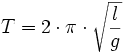Robert Hooke a simplement étendu cette solution au cas à deux dimensions (mouvement plan) : il remarqua qu'en prenant x(t) et y(t) sinusoïdales de même pulsation, le mouvement était une ellipse (dite de Lissajous en France). Ses connaissances en « calculus » étaient quasi-inexistantes ( ? ).

Newton, lui, écrivit (presque comme cela) :

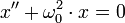
— et —

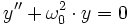
donc

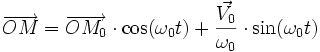
— et —

hodographe 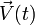invariant par la translation temporelle t → t + T/4

ce qui est la définition d'une ellipse par ses diamètres conjugués, bien connue en géométrie projective (voir cercle en perspective axonométrique) : la construction se fait aisément à la règle et au compas. (épure promise dès que je sais dessiner).

Les théorèmes d'Apollonius y retrouvent une interprétation physique simple (énergie E₀, moment cinétique L₀). De plus, il existe un invariant tensoriel supplémentaire, auquel correspond en mécanique quantique une dégénérescence des niveaux d'énergie (cf. symétrie).

Dans le cas d'une boule homogène, le champ de gravité interne est

avec

k = m·g/R

de sorte que la trajectoire interne d'une petite masse serait une ellipse de Hooke de période

,

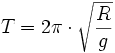qui est donc indépendante du rayon de la boule, mais seulement de sa masse volumique, résultat qui n'étonne pas celui qui connaît le théorème de Newton-Gauss sur les coques creuses :

la masse au-delà de l'apogée de la trajectoire est sans action de gravité.

Hooke avait-il intuité ce théorème avant Newton ? La destruction en 1703 des archives de Hooke par Newton à la Royal Society est bien du caractère de Newton, mais laisse peu de chance pour pouvoir conclure.

Le modèle de Thomson dit de l'électron lié élastiquement

En physique atomique, on utilise par commodité le modèle de Thomson : un électron se déplacerait dans une boule uniforme de charge opposée de rayon environ 0,1nm. Évidemment, on peut dire aussi que c'est l'enveloppe sphérique de l'électron « délocalisé » qui se déplace en bloc par rapport au noyau quasi-ponctuel (on fait de toute façon intervenir la masse réduite). Ce modèle a le bon goût de s'adapter à moult explications en physique atomique, et est donc très utilisé dans l'enseignement.

C'est donc la transposition exacte en électricité d'un écrit de Hooke de 1679.

Notes