Exégèse Des Principia

Les Principia sont une œuvre tellement indigeste qu'il convient de s'atteler à en faire la critique : cela ne remet aucunement en question l'imagination et la puissance de travail de Newton. Récemment une relecture des méthodes nouvelles de la mécanique céleste de Henri Poincaré a été effectuée, sans remettre en cause Poincaré. En 2005, une relecture de la littérature de la relativité restreinte autour de 1905 n'a pas été inutile, quand elle a été libérée de toute passion.

Il s'agit simplement de démystifier l'œuvre : il n'est pas bon en science de louer une œuvre et de ne pas aider à la faire lire. Cet article pourrait s'intituler : pour lire les Principia.

La notation utilisera celle usuelle : traduction de Cohen: "variorum" ou plus simplement "var" ; traduction Cotes-Cajori : "principles" ou plus simplement "princ" ; traduction de la marquise du Châtelet : "cat".

Sommaire 1 Pourquoi lire les Principia ? 2 Comment procéder ? 2.1 Un exemple : Lecture de la Proposition.VI 3 Quelques Corollaires 4 Corollaire sur la Transmutation de la force 5 Bibliographie 6 Voir aussi

Pourquoi lire les Principia ?

1. En France, la lecture du principe fondamental de la dynamique est légèrement différente de celle de l'Angleterre, pour des raisons historiques, qui remontent sans doute à Descartes versus Locke. Le De gravitatione de Newton en est une explication partielle par Newton, lui-même.
2. On sait que Newton a entretenu des rapports tendus avec Hooke. Sur la querelle Hooke-Newton, tout ou presque a été dit sur la fameuse lettre de novembre 1679, gràce à Koyré. Mais on connaît peu l'atmosphère intellectuelle 1684-1687. Et a-t-on examiné de près la revendication de Hooke sur la loi de la gravitation universelle ? et sur l'énoncé des « théorèmes remarquables » ( les théorèmes de Gauss-Newton)?
3. On sait que Newton a entretenu des rapports tendus avec Huygens. Le principe du « bateau de Huygens » défendu plus tard par McLaurin n'a jamais été intégré dans les Principia, créant un obstacle épistémologique pour étudier le principe de Relativité Galiléenne : ce qui explique peut-être le caractère très tardif de l'expérience de Foucault ( 1851).
4. Lors des éditions successives(1687, 1713, 1726), des modifications subtiles se sont produites: quels glissements représentaient-ils réellement dans la pensée de Newton et celle des mécaniciens de l'époque (Huygens, Leibniz, Hermann, Jean Bernouilli, Varignon) ?
5. En France, nous restons grandement marqués par l'influence d'Alexandre Koyré ; il convient là encore de se démarquer de ce géant, sans le renier : beaucoup d'études anglaises ont eu lieu ; il convient de les intégrer dans notre culture, particulièrement les études magistrales de Whiteside et de Bernard Cohen.
6. La thèse de François de Gandt a apporté un souffle novateur encore peu exploité : Archimède, disait le Trio de Torricelli, a démontré la formule de l'aire de la surface de la sphère par le calculus (interdit en Grèce) et a donc dû reformuler sa démonstration pour qu'elle soit acceptée. De même, de Gandt soutient que, le temps de réception du calculus ne s'étant pas écoulé, Newton a reformulé son De Motu en langage géométrique (plus la limite de l'ultime raison (le 0/0, pour dire bref)), puis a demandé du temps pour écrire proprement les Principia. Le très beau livre de Chandrasekhar explique un peu cela, mais reste peu diffusé en France (mais ce n'est pas du tout un livre d'histoire des sciences). De même que le Dana Densmore (Newton's principia : the central argument, (ISBN 1-888-009-00-4)).

Comment procéder ?

Un exemple : Lecture de la Proposition.VI

Soit une trajectoire (T) d'un point matériel P, de masse m, sous l'action d'un champ central de centre O.

Problème : trouver la force m a, agissant en ce point P.

Réponse : Prendre le point Q voisin de P dans le temps ultérieur [dt]. Tracer la demitangente en P ; puis la parallèle à OP, menée de Q, qui vient couper la tangente en R.

Graphiquement, tracer par exemple le segment OP "vertical", P: (x=0;z=10), la portion de tangente PR vers la droite, disons R :(x= 2;z= 8). tracer le segment vertical "descendant" RQ ( Q :(x=2;z=7) ). Fermer le trapèze OPRQ en traçant la droite QO. Finir la figure en traçant l'arc ( ~ parabolique) de la courbe (T), soit arc PQ.

La figure ressemble alors à celle de Torricelli, en 1641(?), dans son livre de Motu, présenté à Castelli, puis envoyé à Galilée.

Le raisonnement va être pratiquement le même, à ceci près que Newton possède une horloge QUI n'EST PAS l'ABSCISSE de R (ou de Q), car le champ est CENTRAL ( or Newton a déjà repéré ce piège en 1679 ( cf déviation vers l'Est) : cette horloge est la LOI des AIRES : aire OPQ = C .dt.

Le raisonnement ensuite est identique : PR = V(P).dt et la chute est RQ: = h = 1/2 a(P). [dt]²:= 1/2 . g .[dt]²

Alors, QUEL QUE SOIT PR , a(P) = 2 RQ / (aire/C)² ; a(P) ne dépend pas de la vitesse V(P)! En prenant des notations à la Torricelli , obtenir alors la formule très simple à retenir :

h := RQ = 1/2. g(P) . [dt]² = 1/2. g(P) . [aire/C]²

Selon les cas, cette aire sera exprimée par 1/2 x(Q).OP, ou via la podaire, comme 1/2 . p.PQ .

Ce théorème est relativement peu connu en France, malgré sa relative simplicité !

Remarquons tout de suite le scaling de la formule : si la courbe est la spirale équiangulaire de Torricelli-Bernouilli, alors h/aire² varie comme 1/r³ ~ g(r) ! c'est la proposition 9 (cf aussi Spirale logarithmique de Newton)!

Quelques Corollaires

Corollaire  : le premier qui vient à l'esprit est de vérifier au moins le cas du cercle, de rayon r, de centre O, c’est-à-dire la formule de Huygens ( Horologium 1657).

On trouve aisément a(P) = 2 C² RQ/(aire)² = .

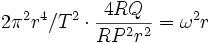C'est initialement cette formule qui donne la troisième loi de Kepler pour une force en 1/r² [ et d'une manière générale 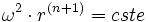pour une loi en 1/r^n ] .

Aussi bien, Newton ne revendiqua-t-il jamais l'antériorité sur la loi en 1/r², mais par contre, les "théorèmes remarquables" de la loi d'attraction universelle sont bien de lui et non de Hooke !

Corollaire, proposition 7 : la trajectoire est un cercle de rayon a, le centre de force sur la circonférence. Faire la figure et déduire immédiatement que h/(aire)² varie comme 1/r^5. (cf Force centrale en 1/r⁵)

Corollaire, la proposition 10, variorum115 : la loi de Hooke en -k/m r donne bien une ellipse de Hooke:

démonstration: h /(aire)² = r/(2p².OD²), avec OD longueur du demi-diamètre conjugué, et p la longueur podaire. Or le théorème VII.31 d'Apollonius (géométrie affine de l'ellipse) dit que l'aire du parallélogramme construit sur 2 demi-diamètres conjugués est constante : p.OD = cste = a.b ; donc g(r) = k r ;CQFD.

Remarque : la symétrie de Corinne donne immédiatement la solution dans le cas répulsif : une hyperbole de centre O.

Remarque 2 : Hooke avait sans doute l'antériorité sur ce problème (< 1684?), via une méthode discrète ( cf mécanique newtonienne discrète )

Corollaire, la proposition 11, variorum125 : la loi en 1/r² redonne bien les lois de Kepler:

C'est ce qui a fait la gloire de Newton dans le deMotu de 1684. Plus exactement, Newton démontre que si (T) est une ellipse de Kepler, alors g(r) = k/r². Il démontrera la réciproque (édition 1713, proposition 17) en utilisant intuitivement le théorème de Cauchy : les deux C.I.(conditions initiales) position, vitesse déterminent une unique ellipse. Attention : chausse-trappe dans le cas de la spirale, et Newton l'évite !

Il faut donc démontrer que le rapport chute/(aire)² ~1/r² : cf mouvement keplerien

Corollaire sur la Transmutation de la force

Célèbre théorème où Newton montre que n'importe quelle trajectoire de champ central S peut être une trajectoire de champ central de centre Q, avec une loi de force différente bien sûr. En particulier, on peut transmuter la loi de Hooke avec centre au centre de l'ellipse, en une loi en 1/ FP², avec pour centre de force le foyer F de l'ellipse : ce théorème fut un féroce pied-de-nez à Hooke, qui ne put jamais s'en remettre : à tout jamais, il fut celui qui n'avait su passer que des ellipses de Hooke aux elliptoïdes; il ne possédait pas la puissance mathématique de Newton, et s'il était très doué en dessin, cela ne lui permettait évidemment pas de passer à la "limite de l'ultime quotient 0/0" !

Rappelons cet énoncé :

• Énoncé : Soit un champ central de centre S de force F(r) produisant un mouvement de trajectoire (T), décrit selon la loi des aires (deuxième loi de Kepler).

Alors, cette même trajectoire (T) existe comme solution d'un problème de champ central de centre S' quelconque (mais dans la concavité de (T), certes), de force F'(r') différente évidemment :

F'(r') = F(r). (facteur de transmutation)

Ce facteur de transmutation vaut : SG^3/(r. r'²), où SG est le segment parallèle au vecteur S'M, situé entre S et la tangente-en-M à la trajectoire (T).

Rappelons la conséquence historique de 1684 : Hooke ⇒ Kepler.

En effet soit S = O centre de l'ellipse et F(r) = - k r (loi dite de Hooke);

Et soit S' = F foyer de la même ellipse, alors SG = cste = a,

le facteur de transmutation devient a³/ (r . r'²) et donc la force centrale de Foyer F est -k a³/r'² en 1/r'² .

Bibliographie

• Brackenridge, Key to Newton's dynamics, 1995, u California p, (ISBN 0-520-20065-9)
• Cohen & Whitman, The Principia: Mathematical Principles of Natural Philosophy, u California p, (ISBN 0-520-08816-6)
• Cordani, The Kepler problem, 2003, ed Birkhauser, (ISBN 3-7643-6902-7)
• Densmore, Newton's Principia, 1995, ed Green Lion Press, (ISBN 1-888009-01-2)
• Guicciardini, Reading the Principia, 1999, CUP, (ISBN 0-521-64066-0)
• Voir aussi les ouvrages de Cohen, Whiteside, Biarnais et De Gandt

Voir aussi

• Force centrale
• Méthode des indivisibles
• Mouvement à force centrale
• Mouvement central discret
• Mouvement keplerien
• Philosophiae Naturalis Principia Mathematica
• Principia et Calculus
• Spirale logarithmique de Newton
• Temps newtonien
• Transmutation de la force

• Portail de la physique