Condensateur (électricité)

Condensateurs électrochimiques (électrolytiques aluminium). Le 1^er est de 1 000 µF pour une tension de service de 35 V (modèle axial), le 2^e est de 10 µF pour 160 V (modèle radial).

Un condensateur est un composant électronique ou électrique élémentaire, constitué de deux armatures conductrices (appelées « électrodes ») en influence totale et séparées par un isolant polarisable (ou « diélectrique »). Sa propriété principale est de pouvoir stocker des charges électriques opposées sur ses armatures. La valeur absolue de ces charges est proportionnelle à la valeur absolue de la tension qui lui est appliquée. Le condensateur est caractérisé par le coefficient de proportionnalité entre charge et tension appelé capacité électrique et exprimée en farads (F). La relation caractéristique d'un condensateur idéal est :

où :

• i est l'intensité du courant qui traverse le composant, exprimée en ampère (symbole A) ;
• u est la tension aux bornes du composant, exprimée en volt (symbole V) ;
• C est la capacité électrique du condensateur, exprimée en farad (symbole F).
• est la dérivée de la tension par rapport au temps.

Les signes sont tels que l'électrode par laquelle entre le courant (dans le sens conventionnel du courant) voit son potentiel augmenter.

Le condensateur est utilisé principalement pour :

• stabiliser une alimentation électrique (il se décharge lors des chutes de tension et se charge lors des pics de tension) ;
• traiter des signaux périodiques (filtrage…) ;
• séparer le courant alternatif du courant continu, ce dernier étant bloqué par le condensateur ;
• stocker de l'énergie, auquel cas on parle de supercondensateur.

Loi de comportement du condensateur

Symbole d'un condensateur non polarisé dans un circuit.

On définit la capacité par la relation :

où :

• Q est la charge stockée sur sa borne positive et s'exprime en Coulombs;
• U est la tension aux bornes du composant ;
• C est la capacité électrique du condensateur.

Expression algébrique de la loi de comportement du condensateur :

Les indices 1 et 2 repérant chacune des bornes. Q_k étant la charge de la borne k et V_k son potentiel électrique (k = 1 ou 2). La borne au potentiel le plus élevé (borne positive) est donc chargée positivement. La charge « totale » d'un condensateur Q_t = Q₁ + Q₂ est donc nulle. Procédant par influence électrostatique, le courant « pénétrant » par une borne ressort à l'identique par l'autre borne, bien que les armatures soient séparées par un isolant.

Si l'on oriente la branche de circuit contenant le condensateur dans le sens : borne 1 → borne 2, fixant ainsi le sens positif du courant i, on définit alors algébriquement la tension u dans le sens opposé (convention récepteur)

u = V₁ − V₂

Il devient alors possible de définir algébriquement une relation entre le courant circulant dans la branche et la dérivée temporelle de la tension :

La valeur de la tension aux bornes du condensateur en régime transitoire en fonction du temps pour un système du premier ordre est définie par la relation suivante:

, V₀ est la tension initiale et est la tension en régime permanent

et τ est la constante de temps qui équivaut à

dans un circuit ayant un condensateur en série avec une résistance. En connaissant les valeurs de tension initiales et finales, on peut en déduire le temps t.

Composant électrique ou électronique

Plusieurs types de condensateurs. De gauche à droite : céramique multicouche, céramique disque, film polyester multicouche, céramique tubulaire, polystyrène, film polyester métallisé, électrolytique aluminium. Unité de mesure en centimètres.

Le mot condensateur peut désigner spécifiquement un composant électrique ou électronique conçu pour pouvoir emmagasiner une charge électrique importante sous un faible volume ; il constitue ainsi un véritable accumulateur d'énergie.

En octobre 1745, Ewald Georg von Kleist de Poméranie inventa le premier condensateur. Le physicien hollandais Pieter van Musschenbroek le découvrit de façon indépendante en janvier 1746. Il l'appela la bouteille de Leyde car Musschenbroek travaillait à l'université de Leyde.

• Un condensateur est constitué fondamentalement de deux conducteurs électriques, ou « armatures », très proches l'un de l'autre, mais séparés par un isolant, ou « diélectrique ».

La charge électrique emmagasinée par un condensateur est proportionnelle à la tension appliquée entre ses deux armatures. Aussi, un tel composant est-il principalement caractérisé par sa capacité, rapport entre sa charge et la tension.

La capacité électrique d'un condensateur se détermine essentiellement en fonction de la géométrie des armatures et de la nature du ou des isolants ; la formule simplifiée suivante est souvent utilisée pour estimer sa valeur :

avec S : surface des armatures en regard, e distance entre les armatures et ε la permittivité du diélectrique.

• L'unité de base de capacité électrique, le farad représente une capacité très élevée, rarement atteinte (à l'exception des supercondensateurs) ; ainsi, de très petits condensateurs peuvent avoir des capacités de l'ordre du picofarad.
• Une des caractéristiques des condensateurs est leur tension de service limite, qui dépend de la nature et de l'épaisseur de l'isolant entrant dans leur constitution. Cet isolant présente une certaine rigidité diélectrique, c'est-à-dire une tension au-delà de laquelle il peut apparaître un violent courant de claquage qui entraîne une destruction du composant (sauf pour certains d'entre eux, dont l'isolant est dit auto-cicatrisant).

La recherche de la plus forte capacité pour les plus faibles volume et coût de fabrication conduit à réduire autant que possible l'épaisseur d'isolant entre les deux armatures ; comme la tension de claquage diminue également dans la même proportion, il y a souvent avantage à retenir les meilleurs isolants.

Désignation	Capacité	Champ électrique	Représentation
Condensateur plan
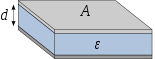
Condensateur cylindrique
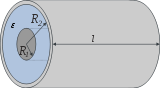
Condensateur sphérique
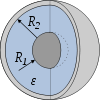
Sphère	C = 4πε0εrR1

où ε₀ représente la permittivité relative du vide (8,84 10-12 Fm-1) et ε_r la permitivité relative de l'isolant.

Les différentes catégories de condensateurs

De nombreuses techniques, souvent issues de la chimie, ont permis d'améliorer sensiblement les performances des condensateurs, que l'on relie à la qualité du diélectrique employé. C'est donc la nature du diélectrique qui permet de classer les condensateurs :

• les condensateurs non polarisés, de faible valeur (nanofarad ou microfarad) sont essentiellement de technologie « mylar » ou « céramique » ;
• les condensateurs dits polarisés sont sensibles à la polarité de la tension électrique qui leur est appliquée : ils ont une borne négative et une positive. Ce sont les condensateurs de technologie « électrolytique » (également appelée, par abus de langage, « chimique ») et « tantale ». Une erreur de branchement ou une inversion accidentelle de la tension conduit généralement à leur destruction, qui peut être très brutale, voire explosive ;
• les supercondensateurs ((en)) non polarisés ont une énorme capacité mais une faible tenue en tension (quelques volts). Ils ont été développés suite aux recherches effectuées pour améliorer les accumulateurs. La capacité qui peut dépasser la centaine de farads est obtenue grâce à l'immense surface développée d'électrodes sur support de charbon actif ;
• les condensateurs à capacité variable, employés par exemple pour la réalisation des filtres RLC réglables.

Quand on rapproche les plaques, la capacité augmente rapidement, de même que le gradient de tension (c'est-à-dire le champ électrostatique). Par exemple, le champ dans un condensateur soumis à seulement 5 volts et dont les plaques sont distantes de 5 micromètres est de 1 million de volts par mètre. L'isolant joue donc un rôle capital. L'isolant idéal aurait une résistance infinie et une transparence totale au champ, n'aurait aucun point d'éclair (gradient de champ où apparaît un arc), n'aurait aucune inductance (qui limite la réaction aux hautes fréquences : un condensateur idéal laisserait passer la lumière par exemple), etc. On doit donc choisir un isolant selon le but recherché, c’est-à-dire l'usage qu'on veut faire du condensateur.

Les condensateurs électrolytiques

Utilisation

Les condensateurs électrolytiques sont utilisés :

• quand on a besoin d'une grande capacité de stockage ;
• quand on n'a pas besoin d'avoir un condensateur parfait ;
  • grande résistance en série,
  • mauvaise réponse aux hautes fréquences,
  • grande tolérance.

Fabrication

Contrairement à tout autre condensateur, lorsqu'on les fabrique, on ne met pas d'isolant entre les deux conducteurs. D'ailleurs, un électrolytique neuf conduit le courant continu. En fait, un des conducteurs est métallique, l'autre est une gelée conductrice : le conducteur métallique est simplement inséré dans la gelée. Lorsqu'on applique une tension pour la première fois, une réaction chimique (appelée électrolyse, d'où le nom) a lieu, ce qui crée une interface isolante à la surface du métal. Évidemment, sitôt formée, cette couche empêche le courant de passer et donc sa propre formation. Il en résulte une couche isolante très mince (quelques molécules d'épaisseur) d'où la très grande capacité des condensateurs électrolytiques en fonction de leur volume. D'où aussi leur tension maximale limitée (quelques centaines de volts). Cependant, la gelée n'est pas aussi bonne conductrice qu'un métal : un condensateur électrolytique a donc une résistance série non négligeable qui crée un « zéro » au sens des fonctions de transfert (filtre passe-bas) avec la capacité. De plus, un courant alternatif passant dans la gelée déforme les orbitales des électrons des couches de valence qui lient la gelée, créant une petite vibration mécanique dans la gelée, d'où :

• un effet d'inertie (inductance) important ;
• une mauvaise réponse aux hautes fréquences.

À l'origine, ces condensateurs n'étaient pas conçus pour servir à des fins de découplage ou de filtrage de signaux. Ils sont principalement utilisés dans la partie filtrage des circuits d'alimentation.

Les condensateurs au tantale

Il existe deux technologies de condensateurs au tantale :

Les condensateurs au tantale à électrolyte solide : ce sont des condensateurs où la première électrode est le tantale, et la seconde du dioxyde de manganèse MnO₂. Le contact avec le dioxyde de manganèse est assuré par une couche de métallisation à base d'argent. Cette technologie apporte les avantages suivants :

• résistance série (ESR) réduite ;
• faibles inductances série ;
• faibles résonances ;
• pas de dégradation dans le temps, en stockage ou en utilisation ;
• coût faible.

Les condensateurs au tantale à électrolyte liquide (WET Tantalum) : ce sont des condensateurs où la première électrode est le tantale, et la seconde un gel conducteur.

• plus de résistance série (ESR) que les modèles « solides » ;
• faibles inductances série ;
• faibles résonances ;
• capacité d'auto-cicatrisation élevée, d'où une grande fiabilité ;
• coût plus élevé.

En effet, l'électrolyte liquide est capable d'oxyder le tantale en cas de défaut dans la couche d'oxyde, cette régénération en fait des condensateurs de grande fiabilité, ils sont souvent choisis pour des applications où la fiabilité est un critère déterminant ; exemple : utilisation dans un satellite. Par contre, cette possibilité signifie qu'un courant de fuite plus élevé est possible, à prendre en compte dans la conception.

Les condensateurs à électrolyte liquide sont plus coûteux, en raison des matériaux utilisés : argent ou encore tantale massif pour le boîtier (à cause de l'électrolyte acide), ainsi que des procédés de fabrication plus complexes (assemblage étanche), ils sont de fait réservés à des applications « haut de gamme ».

Les condensateurs au tantale solide présentent une résistance série extrêmement faible, ce qui en fait un composant préférentiel pour les découplages d'alimentation sur les cartes.

Les condensateurs au tantale ont toutefois un défaut : il présentent une légère non-linéarité, c'est pourquoi ces condensateurs sont déconseillés pour la transmission de signaux (création d'harmoniques paires) sauf lorsqu'ils sont associés à d'autres condensateurs non électrolytiques pour former un condensateur composite.

Les condensateurs au tantale solide ont également un autre défaut : le tantale risque de prendre feu en cas de dépassement du courant ou en cas de défaillance. C'est pourquoi ils sont peu utilisés dans des applications où cela présente un danger pour l'utilisateur (automobile par exemple).

Modélisation

Un condensateur électrolytique se modélise de façon plus ou moins réaliste.

• En première approximation, on décrit les caractéristiques essentielles du composant :
  • la valeur de la capacité ;
  • la résistance série ;
  • l'inductance série ;
  • la résistance parallèle ;
• En faisant une modélisation plus sophistiquée, on accède à des caractéristiques plus fines :
  • l'hystérésis de charge ;
  • l'effet de batterie ;
  • autres (influence de la température, le vieillissement des matériaux, etc.).

L'hystérésis de charge est un effet qui fait que, en deçà d'une tension seuil (faible), la gelée ne laisse pas passer de courant (par exemple, un gros condensateur électrolytique de 1 farad soumis à une tension de 5 microvolts n'accumulera pas une charge de 5 microcoulombs). Il en résulte donc que les faibles signaux alternatifs en ressortent avec une distorsion qui ressemble à celle d'un amplificateur classe B pure, quoique beaucoup moindre.

L'effet de batterie, moins négligeable, est dû à l'existence d'une réaction d'électrolyse et une d'électrosynthèse parasites qui ont lieu en présence d'un signal alternatif ou d'une tension continue. Cette charge et décharge de batterie est à ne pas confondre avec une charge et décharge de condensateur, car sa constante de temps est beaucoup plus grande. Pour l'observer, on peut charger un condensateur électrolytique, le laisser chargé quelques minutes (ce qui provoque le phénomène) puis le décharger brusquement en le court-circuitant pendant un court moment. Au moyen d'un voltmètre, on observera alors aux bornes la réapparition d'une tension : c'est la charge de batterie.

Un autre effet de cette technologie est que la couche isolante n'a pas toujours la même épaisseur, même pour un même modèle. L'épaisseur dépend de plusieurs facteurs : la température, les micro-aspérités microscopiques du métal, les vibrations, l'humidité lors de la fabrication, l'âge du condensateur, l'usage auquel il a été soumis, etc. C'est pourquoi la capacité des électrolytiques est toujours présentée avec une grande tolérance (typiquement –20 % à +100 % pour les gros), ce qui en fait des mauvais candidats pour faire des filtres précis ou des bases de temps.

Les condensateurs à isolant

Ils sont fabriqués selon la définition classique du condensateur : un conducteur métallique séparé d'un isolant. Comme toujours, l'isolant, choisi en fonction de l'usage qu'on veut en faire, déterminera la nature du condensateur.

Air

Cette catégorie comprend les condensateurs variables/ajustables et certaines capacités de faible valeur réalisées à l'aide du circuit imprimé lui-même. Ses caractéristiques d'isolation sont relativement faibles et sensibles à l'humidité ambiante.

Exemple :

• condensateur ajustable à air (utilisés dans les postes récepteurs de radio pour le choix des stations).

Ils sont constitués d'armatures mobiles l'une par rapport à l'autre ; les surfaces en regard déterminent la valeur du condensateur.

Céramique

La céramique présente :

• les avantages d'une inductance extrêmement faible et d'une très grande résistance série, c'est pourquoi les condensateurs à isolant de céramique sont largement utilisés :
  • dans les applications haute fréquence (jusqu'à des centaines de gigahertz) ;
  • dans les applications haute tension (circuits à valves (tubes) par exemple) ;
  • pour les composants de surface, car ils se prêtent bien à une miniaturisation.

• les inconvénients :
  • d'être mécaniquement fragile ;
  • d'avoir un champ d'éclair pas très élevé. Ils nécessitent une certaine distance entre les plaques et se prêtent donc mal aux grandes capacités (ce qui n'a pas d'importance dans les hautes fréquences) ;
  • ils ont une légère hystérésis de charge et génèrent un tout petit peu de bruit lorsque le dV/dt (courant donc) est élevé (grande amplitude de signal ou très haute fréquence). Ce bruit étant un bruit blanc a peu d'effet sur les circuits haute fréquence, ceux-ci étant généralement accordés (syntonisés) sur une bande étroite.

Plusieurs classes de céramiques sont définies selon leur tenue en température^[1] :

• les céramiques C0G ou NP0 présentent une grande stabilité et sont utilisées pour les applications de haute fréquence, et chaque fois que l'on exige une bonne stabilité en température. Malheureusement, ces céramiques ne présentent pas une très grande constante diélectrique, ce qui limite la valeur de la capacité : classiquement quelques nanofarads au maximum, pour les composants de surface ;
• les céramiques X7R, de stabilité moindre : environ 10 % de variation entre -10 °C et +60 °C. On réserve ces céramiques aux applications n'exigeant pas une haute stabilité. La constante diélectrique est plus élevée, ce qui permet d'atteindre en standard CMS des capacités de quelques centaines de nanofarads ;
• les céramiques Y4T et Z5U, ont des dérives en température de l'ordre de 50 % dans les gammes citées plus haut, et sont donc réservées aux fonctions de découplage. Par contre on peut obtenir des capacités en composants de surface, de plusieurs microfarads ;
• les céramiques particulières pour les hyperfréquences, de très haute stabilité et de très faible facteur de perte. Ces céramiques ont un coût nettement supérieur, mais sont indispensables pour certaines applications.

Condensateurs film à base de matériaux synthétiques

Les condensateurs à isolant plastique (polyéthylène, polystyrène et polypropylène sont les plus courants) ont été conçus spécifiquement pour fins de découplage de signaux et d'utilisation dans des filtres^[2]. Leur hystérésis de charge est très faible (nul pour le polypropylène) et, de ce fait, ils sont précieux pour le traitement de très faibles signaux (radiotélescopes, communications spatiales et… audio de référence). Le polystyrène et le polypropylène n'ont pas d'effet de batterie (le polyéthylène en a un très faible).

Construction

Deux méthodes sont utilisées : soit par l'utilisation de feuilles conductrices et isolantes (film/foil construction), soit par dépôt d'aluminium sur le diélectrique (metallized film capacitor). La deuxième méthode diminue le coût, le volume, le poids des condensateurs, mais diminue également le courant admissible^[3].

Polyester

Le polyester est principalement utilisé sous deux de ses formes : le polyéthylène téréphtalate (PET), et le polyéthylène naphtalate (PEN)^[4]

L'avantage du polyéthylène est qu'il peut être étiré (ou laminé) très mince et peut donc permettre des capacités appréciables dans un petit volume (pas comparables aux électrolytiques, cependant). Il est facile à manufacturer et à former, et ces condensateurs sont donc peu coûteux. Les condensateurs à polyéthylène sont très employés dans les circuits audio de moyenne à bonne qualité et dans des circuits demandant une faible variation de capacité avec l'âge et l'humidité.

Polystyrène

Le polystyrène n'est pas aussi facile à fabriquer avec précision que le polyéthylène. Il n'est pas coûteux en soi (des emballages sont faits de polystyrène) mais difficile à laminer précisément en couches minces. Pour cette raison, les condensateurs en polystyrène sont relativement encombrants pour une capacité donnée (un 0,01 µF étant aussi volumineux qu'un électrolytique de 200 µF). Ils sont aussi nettement plus coûteux que les polyéthylènes.

Le grand avantage des condensateurs en polystyrène est leur qualité. Ils sont très stables. Pour cette raison, ils sont employés là où la précision est requise : circuits syntonisés à bande étroite, bases de temps, etc. Leur bruit est pratiquement indécelable et très proche de la limite théorique (limite de Johnson). Ils sont très peu sensibles à la température et à l'âge et, pour autant qu'on reste en deçà des limites de courant et tension du manufacturier, insensibles à l'usage. Leur inductance parasite dépend du montage : certains sont faits de deux feuilles de métal et deux feuilles de polystyrène enroulées en spirale : ceux-là présentent une bonne précision de la capacité au prix d'une certaine inductance parasite (faible). D'autres sont faits de plaques moulées dans un bloc de polystyrène : ils sont moins précis pour la capacitance (ce qui n'est pas un problème pour les circuits de précision qui ont toujours un élément ajustable) mais ont une inductance parasite extrêmement faible.

Polypropylène

Les condensateurs polypropylène (PP) sont très utilisés en audio et dans les applications impulsionnelles (alimentations à découpage, circuits d'aide à la commutation, etc.) car ils sont caractérisés par une résistance série très faible et admettent donc des courants efficaces importants. Ils sont aussi moins chers que les condensateurs au polystyrène (le polypropylène est très connu des manufacturiers de plastique : beaucoup de jouets, de meubles, boîtiers divers, pièces automobiles, téléphones portables et autres accessoires, même les sacs d'épicerie, sont faits de polypropylène). Ils sont aussi stables que le polystyrène. Ils sont moins précis en valeur nominale que les condensateurs au polystyrène (ils ne sont pas utilisés dans les circuits de référence comme par exemple les bases de temps précises). Ils sont aussi assez volumineux pour leur capacité, le polypropylène se prêtant mal, lui aussi, à un laminage très fin.

Mica

Ces condensateurs, généralement de faible valeur, sont utilisés en haute fréquences et en moyenne et haute tension. Ils ont une bonne stabilité (étalon de mesure, etc.), mais ils coûtent environ deux fois plus cher qu'un condensateur céramique de tension et capacité égale par exemple.

Autres matériaux

On trouve également du polyphénylène sulfide (PPS), polycarbonate (PC) (condensateurs de précision), polyimide (PI), téflon (Polytetrafluoroéthylène PTFE)^[5].

Papier

Les condensateurs à film papier ont été utilisés dans les anciens récepteurs radio. Ils ont été abandonnés du fait de leur mauvais vieillissement, entraînant un important courant de fuite. On peut souvent en trouver chez des luthiers, les guitaristes adeptes de son vintage les utilisent parfois sur les guitares électriques.

Verre

Les condensateurs multicouches avec un diélectrique en verre sont utilisés pour leur stabilité en température et en durée de vie^[6].

Séries de valeurs normales

La liste des valeurs disponibles est définie par la norme CEI 60063.

Tension de claquage

Lorsqu’on maintient une tension u entre les bornes d’un condensateur plan, il s’établit entre ses armatures, distantes de d, un champ électrique uniforme Е perpendiculaire aux armatures. Chaque diélectrique est caractérisé par un champ électrique qu’il peut supporter. Ce champ, appelé champ disruptif constitue la limite au-delà de laquelle une étincelle jaillit entre les deux armatures provoquant la décharge du condensateur accompagné généralement de sa détérioration : c’est le claquage du condensateur.

Marquage

La valeur des condensateurs électroniques est marquée sur leurs boîtiers sous quatre formes principales. Elle est en clair sur les condensateurs de grosseur suffisante pour accueillir l'inscription (exemple : 10 µF). Le caractère µ est parfois transformé en la lettre u comme dans 10 uF. Le fabricant peut utiliser le code de couleurs CEI 60757 relativement peu employé sauf sur certains condensateurs en boîtier plastique. Le plus souvent sur les condensateurs de taille modeste et de précision normale, la valeur est notée en picofarads (pF) dans le format XXY où XX correspond aux deux premiers chiffres de la valeur et Y à la valeur de l'exposant de dix en notation scientifique^[7]. Par exemple, un marquage de 474 signifie 47×10⁴ pF ( 47×10⁴ x 1×10^-12 F = 47×10^-8 F), soit 470 nF. Autres exemples : 101 correspond à 100 pF, 220 à 22 pF ; 684 signifie 680 000 pF soit 680 nF ou 0,68 µF. La dernière manière de marquer la valeur capacitive sur les condensateurs ressemble à la première, elle est en "clair" pour autant que l'on sache que l'unité de lecture est le microfarad [µF]. S'il est marqué d'un 4,7 cela signifie 4,7  µF, autres exemples : 68 correspond à 68 µF ou encore 0,022 correspond à 22 nF en d'autres termes, si la valeur marquée est décimale ou d'un nombre à 2 chiffres, la valeur se lit en microfarad.

Calcul des circuits comportant un ou des condensateur(s)

L'intensité qui circule dans la branche où est présent un condensateur, ne dépend pas directement de la tension aux bornes de ce condensateur, mais de la variation de cette tension. Ainsi, on écrit généralement l'équation (en convention récepteur, q étant la charge de l'armature sur laquelle arrive i) :

q étant la charge de l'armature en coulomb.

C étant la capacité du condensateur en farad.

On peut ainsi en déduire l'impédance du condensateur alimenté par une tension fonction sinusoïdale du temps  :

où U et I sont les valeurs efficaces des grandeurs u et i

La transformation complexe appliquée à la tension et à l'intensité permet de déterminer l'impédance complexe :

Ces relations montrent bien qu'un condensateur se comporte comme un circuit ouvert (impédance infinie) pour une tension continue et tend à se comporter comme un court-circuit (impédance nulle) pour les hautes fréquences. Pour ces raisons, ils sont utilisés pour réaliser des filtres, parfois en association avec des inductances.

Énergie stockée - puissance échangée

Un condensateur stocke de l'énergie sous forme électrique.

Cette énergie E (Joule) s'exprime en fonction de sa capacité C (Farad) et de sa charge q (Coulomb) (ou de sa tension u) selon :

On remarque que cette énergie est toujours positive (ou nulle) et qu'elle croît comme le carré de la charge ou de la tension.

Ces propriétés sont analogues à celles de l'énergie cinétique d'une masse m animée d'une vitesse v.

Démonstration

On sait que q = Cu

Une autre façon de voir en calculant directement l’Énergie :

Avec :

u[0] = 0

on obtient aussi le résultat escompté :

 

La puissance électrique P reçue par le condensateur est la dérivée par rapport au temps de cette énergie.

On reconnaît dans la dernière égalité, l'expression générale de la puissance électrique reçue par un dipôle (en convention récepteur).

Si la puissance est positive (puissance reçue) cette énergie augmente, le condensateur se charge. Inversement lorsque le condensateur se décharge, l'énergie diminue, la puissance est négative : elle est cédée par le condensateur au monde extérieur.

Il en résulte qu'il est difficile de faire varier rapidement la tension aux bornes d'un condensateur et ceci d'autant plus que la valeur de sa capacité sera élevée. Cette propriété est souvent utilisée pour supprimer des variations de tension non désirées (filtrage).

Inversement, une décharge très rapide d'un condensateur dans une utilisation de faible résistance électrique est possible. Une énergie importante est délivrée dans un temps très court (donc avec une très forte puissance). Cette propriété est entre autres exploitée dans les flashs électroniques et dans les alimentations de lasers pulsés.

Il est préférable de parler de puissance reçue (ou cédée) plutôt que de puissance consommée.

Ce dernier qualificatif laisse à penser que la puissance reçue est « perdue » ou du moins dissipée. Ce qui est le cas d'une résistance qui « consomme » de la puissance électrique, toujours positive par effet Joule, la puissance Joule « consommée » s'écrivant :

Lois d'association

Association en parallèle

Lorsque deux condensateurs sont placés en parallèle, donc soumis à la même tension, le courant à travers cet ensemble est la somme des courants à travers chacun des condensateurs. Ceci a pour conséquence que la charge électrique totale stockée par cet ensemble est la somme des charges stockées par chacun des condensateurs qui le composent :

donc :

Ce raisonnement est généralisable à n condensateurs en parallèle : le condensateur équivalent à n condensateurs en parallèle a pour capacité la somme des capacités des n condensateurs considérés.

La tension maximale que peut supporter l'ensemble est celle du condensateur dont la tension maximale est la plus faible.

Association en série

Lorsque deux condensateurs sont en série, donc soumis au même courant, il en résulte que la charge stockée par chacun d'eux est identique.

ou

d'où

Ce raisonnement étant généralisable à n condensateurs, on en déduit que le condensateur équivalent à n condensateurs en série a pour inverse de sa capacité la somme des inverses des capacités des n condensateurs considérés.

Cette association est généralement une association de n condensateurs identiques ayant pour but d'obtenir un ensemble dont la tension maximale qu'il peut supporter est égale à n fois celle des condensateurs utilisés, ceci au prix d'une division de la capacité par n.

Modélisation en haute fréquence

Les condensateurs sont très souvent utilisés dans les circuits de hautes fréquences. Sur ces fréquences, les éléments parasites peuvent changer notablement les valeurs calculées. En général, jusqu'aux fréquences de quelques gigahertz, deux éléments parasites doivent être pris en compte : L'inductance du boîtier et la résistance équivalente série. L'introduction de ces deux éléments parasites est indispensable, notamment pour la simulation des circuits au-delà de quelques centaines de MHz.

On peut considérer aujourd'hui que l'immense majorité des condensateurs utilisés en hautes fréquences sont en céramique et en composants de surface. C'est donc surtout ce type de condensateur qui est envisagé ici.

Le modèle d'un condensateur CMS sera donc constitué par trois éléments en série : la capacité nominale C, la résistance équivalente série Rs et l'inductance du boîtier L.

La résistance Rs est constituée non seulement de la résistance ohmique, mais aussi de la résistance série fictive représentant les pertes diélectriques. Pour les condensateurs avec céramique NP0, la valeur de cette résistance sera comprise en général entre 0,1 et 1 ohm. Si on veut des résistances rs plus faibles, notamment pour réduire les pertes des filtres en VHF et UHF, on devra utiliser les condensateurs dits « high Q », et au-delà de 2 ou 3 GHz, il faudra utiliser uniquement des condensateurs spécifiés pour hyperfréquences… ou des condensateurs répartis réalisés avec le circuit imprimé lui-même.

L'inductance série va varier avec le boîtier (elle est augmentée aussi de l'inductance des pistes, dont on ne parle pas ici…). Pour les boîtiers CMS 1206, cette inductance est de l'ordre de 2 nH. Pour un boîtier 0603, elle sera plutôt de l'ordre de 0,5 nH. Pour se convaincre de l'importance de cette inductance, il suffit de vérifier qu'à 1,5 GHz, un condensateur de 10 pF en boîtier 1206 n'est plus une capacité mais une inductance.

Une modélisation plus fine consiste à modéliser le condensateur et sa piste comme une ligne plutôt qu'une inductance. On devra alors calculer l'impédance caractéristique de la ligne, fonction de la largeur du condensateur et de la piste, et de l'épaisseur du substrat sur lequel il est posé.

Innovations et prospective

Un nouveau condensateur cylindrique (40 mm de diamètre, 110 mm de long, pour une tension de 3,8 V à 2,2 V ) au lithium, produit par le japonais Shin-Kobe Electric Machinery offre selon le fabricant une faible auto-décharge (2% en 1 000 heures à 60 °C), pour une densité énergétique de 10,1 Wh/l (équivalent à une capacité de 1,37 Wh) en pouvant être traversé par des courants élevés (jusqu'à 300 A). Sa température de fonctionnement est comprise entre -20 °C et +80 °C^[8].

Notes et références

Bibliographie

• (en) Principles and Applications of Electrical Engineering (voir formule 1.1)

Voir aussi

Articles connexes

• Capacité électrique
• Nanocondensateur
• Supercondensateur
• Circuit RC
• Circuit LC
• Circuit RLC
• Décharge d'un condensateur
• Coltan

• Portail de l’électricité et de l’électronique