Circuit RC

Pour les articles homonymes, voir RC.

Un circuit RC est un circuit électrique, composé d'une résistance et d'un condensateur montés en série ou en parallèle. Dans leur configuration série, les circuits RC permettent de réaliser des filtres électroniques passe-bas ou passe-haut. La constante de temps $τ$ d'un circuit RC est donnée par le produit de la valeur de ces deux éléments qui composent le circuit.

Circuit série

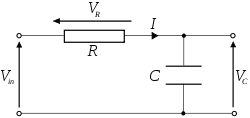
Circuit RC série

Fonctions de transfert

Soit $Z C (ω)$ l'impédance du condensateur :

$Z_C(\omega) = \frac {1}{jC\omega}$

La tension aux bornes de la résistance ou du condensateur peut se calculer en considérant le montage comme un diviseur de tension non chargé :

$V_C(\omega) = \frac {Z_C(\omega)}{Z_C(\omega) + R} V_{in}(\omega) = \frac {1}{1+jRC\omega} V_{in}(\omega)$

$V_R(\omega) = \frac {R}{Z_C(\omega) + R} V_{in}(\omega) = \frac {jRC\omega}{1+jRC\omega} V_{in}(\omega)$ .

On notera $H C$ la fonction de transfert obtenue en considérant la tension aux bornes du condensateur comme tension de sortie et $H R$ si on utilise celle aux bornes de la résistance. $H C$ et $H R$ s'obtiennent respectivement grâce aux expressions de $V C$ et $V R$ :

$H_C(\omega) = { V_C(\omega) \over V_{in}(\omega) } = { 1 \over 1 + jRC\omega }$

$H_R(\omega) = { V_R(\omega) \over V_{in}(\omega) } = { jRC\omega \over 1 + jRC\omega }$

Pour un dipôle, on peut écrire la fonction de transfert sous la forme $H(\omega) = G e^{j \varphi}\,$ , où $G\,$ est le gain du dipôle et $\varphi\,$ sa phase. Ainsi :

$H_C(\omega) = G_C e^{j \varphi_C}$

avec

$G_C = \frac{1}{\sqrt{1 + \left(\omega RC\right)^2}}$

$\varphi_C = \arctan \left(-\omega RC\right)$

De même pour $H R$ :

$H_R(\omega) = G_R e^{j \varphi_R}$

avec

$G_R = \frac{\omega RC}{\sqrt{1 + \left(\omega RC\right)^2}}$

$\varphi_R = \arctan \left(\frac{1}{\omega RC}\right)$ ,

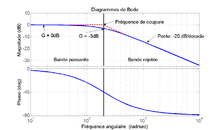
Analyse fréquentielle

Lieux de Bode de

H C

Une analyse fréquentielle du montage permet de déterminer quelles fréquences le filtre rejette ou accepte. Pour les basses fréquences, $H C$ a un module proche de un et une phase proche de zéro . Plus la fréquence augmente, plus son module diminue pour tendre vers zéro et sa phase de $- π / 2$ . A contrario, $H R$ possède un module proche de zéro aux basses fréquences et une phase proche de $π / 2$ et lorsque la fréquence augmente, son module tend vers un et sa phase vers zéro.

Quand $\omega \to 0$ :

$G_C \to 1$ et $\varphi_C \to 0$ .

$G_R \to 0$ et $\varphi_R \to 90^{\circ} = \pi/2$ .

Quand $\omega \to \infty$ :

$G_C \to 0$ et $\varphi_C \to -90^{\circ} = -\pi/2$

$G_R \to 1$ et $\varphi_R \to 0$ .

Ainsi, lorsque la sortie du filtre est prise sur le condensateur le comportement est du type filtre passe-bas : les hautes fréquences sont atténuées et les basses fréquences passent. Si la sortie est prise sur la résistance, l'inverse se produit et le circuit se comporte comme un filtre passe-haut.

La fréquence de coupure $f c$ du circuit qui définit la limite à 3 dB entre les fréquences atténuées et celles qui ne le sont pas est égale à :

$f_c = \frac{1}{2\pi RC}$ (en Hz)

Analyse temporelle

Pour des raisons de simplicité, l'analyse temporelle s'effectuera en utilisant la transformée de Laplace p. En supposant que le circuit est soumis à un échelon de tension d'amplitude V en entrée ( $V_{in} = 0\,$ pour $t = 0\,$ et $V_{in} = V\,$ sinon) :

$V_{in}(p) = \frac{V}{p}$

$V_C(p) = H_C(p)V_{in}(p) = \frac{1}{1 + pRC} \frac{V}{p}$

$V_R(p) = H_R(p)V_{in}(p) = \frac{pRC}{1 + pRC}\frac{V}{p}$ .

La transformée de Laplace inverse de ces expressions donne :

$V_C(t) = V\left(1 - e^{-t/RC}\right)$

$V_R(t) = Ve^{-t/RC}\,$ .

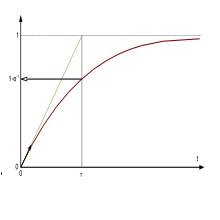
Dans ce cas, le condensateur se charge et la tension à ses bornes tend vers V, tandis que celle aux bornes de la résistance tend vers 0.

Détermination graphique de

τ

par l'observation de

V C (t)

Le circuit RC possède une constante de temps, généralement notée $\tau = RC\,$ , représentant le temps que prend la tension pour effectuer 63 % ( $1 - e - 1$ ) de la variation nécessaire pour passer de sa valeur initiale à sa valeur finale.

Il est également possible de dériver ces expressions des équations différentielles décrivant le circuit :

$\frac{V_{in} - V_C}{R} = C\frac{dV_C}{dt}$

$V_R = V_{in} - V_C\,$ .

Les solutions sont exactement les mêmes que celles obtenues par la transformée de Laplace.

Intégrateur

À haute fréquence, c’est-à-dire si $\omega >> \frac{1}{RC}$ , le condensateur n'a pas le temps de se charger et la tension à ses bornes reste faible.

Ainsi :

$V_R \approx V_{in}$

et l'intensité dans le circuit vaut donc :

$I \approx \frac {V_{in}}{R}$ .

Comme,

$V_C = \frac{1}{C}\int_{0}^{t}Idt$

on obtient :

$V_C \approx \frac{1}{RC}\int_{0}^{t}V_{in}dt$ .

La tension aux bornes du condensateur intègre donc la tension d'entrée et le circuit se comporte comme un montage intégrateur, c'est-à-dire comme un filtre passe-bas.

Dérivateur

À basse fréquence, c’est-à-dire si $\omega << \frac{1}{RC}$ , le condensateur a le temps de se charger quasiment complètement.

Alors,

$I \approx \frac{V_{in}}{1/j\omega C}$

$V_{in} \approx \frac{I}{j\omega C} \approx V_C$

Maintenant,

$V_R = IR = C\frac{dV_C}{dt}R$

$V_R \approx RC\frac{dV_{in}}{dt}$ .

La tension aux bornes de la résistance dérive donc la tension d'entrée et le circuit se comporte comme un montage dérivateur, c'est-à-dire comme un filtre passe-haut.

Intensité

L'intensité du courant est la même dans tout le circuit, puisqu'il s'agit d'un circuit série :

$I(\omega) = \frac{V_{in}(\omega) }{R+Z_C} = { jC\omega \over 1 + jRC\omega } V_{in}(\omega)$

Réponse impulsionnelle

La réponse impulsionnelle est la transformée de Laplace inverse de la fonction de transfert correspondante et représente la réponse du circuit à une impulsion.

Pour le condensateur :

$h_C(t) = {1 \over RC} e^{-t / RC} u(t) = { 1 \over \tau} e^{-t / \tau} u(t)$

où $u(t)\,$ est la fonction de Heaviside et $\tau \ = \ RC$ est la constante de temps.

Pour la résistance :

$h_R(t) = - {1 \over RC} e^{-t / RC} u(t) = - { 1 \over \tau} e^{-t / \tau} u(t)$

Circuit parallèle

Circuit RC parallèle

Le circuit RC parallèle est généralement d'un intérêt moindre que le circuit RC série : la tension de sortie étant égale à la tension d'entrée, il ne peut être utilisé comme filtre qu'alimenté par une source de courant.

Les intensités dans les deux dipôles sont :

$I_R = \frac{V_{in}}{R}$

$I_C = j\omega CV_{in}\,$ .

Le courant dans le condensateur est déphasé de 90° par rapport au courant d'entrée (et de la résistance).

Soumis à un échelon de tension, le condensateur se charge rapidement et peut être considéré comme un circuit ouvert, le circuit se comportant dès lors comme une simple résistance.

Voir aussi

Sur les autres projets Wikimedia :

« Étude des systèmes électriques », sur Wikiversity (communauté pédagogique libre)

Portail de la physique
Portail de l’électricité et de l’électronique

Catégorie :

Circuit électrique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Circuit RC de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

circuit — [ sirkɥi ] n. m. • 1257; circuite n. f. 1220; lat. circuitus, de circuire, circumire « faire le tour » 1 ♦ Vieilli Distance à parcourir pour faire le tour d un lieu. ⇒ contour, périmètre, pourtour, 3. tour. Le parc a quatre kilomètres de circuit … Encyclopédie Universelle
Circuit — may mean: In science and technology Circuit theory, the theory of accomplishing work by routing electrons, gas, fluids, or other matter through a loop Pneumatic circuit Hydraulic circuit Boolean circuit circuit (computer theory) Integer circuit a … Wikipedia
Circuit — Cir cuit, n. [F. circuit, fr. L. circuitus, fr. circuire or circumire to go around; circum around + ire to go.] 1. The act of moving or revolving around, or as in a circle or orbit; a revolution; as, the periodical circuit of the earth round the… … The Collaborative International Dictionary of English
Circuit TI — Circuit international d Okayama 34°54′54″N 134°13′16″E / 34.915, 134.22111 … Wikipédia en Français
circuit — cir·cuit n 1 a: a route formerly taken by traveling judges b: a district established within a state or the federal judicial system see also the judicial system in the back matter 2 cap: the court of appeals for a circuit in the federal judicial… … Law dictionary
circuit — CIRCUÍT, circuite, s.n. 1. Ansamblu de fire şi dispozitive bune conducătoare de electricitate care, împreună cu sursa curentului, formează un traseu închis pentru trecerea unui curent. ♢ (electron.; în sintagma) Circuit imprimat = circuit… … Dicționar Român
circuit — CIRCUIT. sub. mas. (Ce mot est de trois syllabes.) Enceinte, tour. Le circuit de la Ville. Faire le circuit des murailles. Le circuit d une Province. Un grand circuit. Un long circuit. Cette Ville a une grande lieue de circuit. [b]f♛/b] On dit… … Dictionnaire de l'Académie Française 1798
circuit — CIRCUIT. s. m. Enceinte, tour. Le circuit de la ville. faire le circuit des murailles. le circuit d une Province. un grand circuit. un long circuit. cette ville a une grande lieüe de circuit. On dit fig. Circuit de paroles, & cela se prend pour… … Dictionnaire de l'Académie française
circuit — UK US /ˈsɜːkɪt/ noun [C] ► IT a path for an electric current to flow through: »The most advanced chip technology, which uses circuits 65 nanometers apart, loses almost half of its power to leakage. »an electrical/electronic circuit → See also… … Financial and business terms
circuit — [sʉr′kit] n. [ME < OFr < L circuitus, a going around, circuit < circumire < circum (see CIRCUM ) + ire, to go: see YEAR] 1. the line or the length of the line forming the boundaries of an area 2. the area bounded 3. the act of going… … English World dictionary
circuit — (n.) late 14c., from O.Fr. circuit (14c.), from L. circuitus a going around, from stem of circuire, circumire go around, from circum round (see CIRCUM (Cf. circum )) + ire to go (see ION (Cf. ion)). Electrical sense is from 1 … Etymology dictionary

Dictionnaires et Encyclopédies sur 'Academic'

Circuit RC

Sommaire