Spectroscopie RMN

Pour les articles homonymes, voir RMN.

Spectromètre RMN 200 MHz avec passeur automatique d'échantillons utilisé en chimie organique pour la détermination des structures chimiques.

La spectroscopie RMN est le nom donné à une technique qui exploite les propriétés magnétiques de certains noyaux atomiques. Elle est basée sur le phénomène de résonance magnétique nucléaire^{[note 1]}, exploité également en imagerie médicale sous le nom d' IRM. Les applications les plus importantes pour la chimie organique sont la RMN du proton et du carbone-13 effectuée sur des solutions liquides. Mais la RMN est aussi applicable à tout noyau possédant un spin non nul, que ce soit dans les solutions liquides ou dans les solides.

Contrairement à la spectroscopie RMN des solutions qui est utilisée de manière routinière dans les laboratoires académiques ou industriels, la RMN des solides reste légèrement moins abordable sans une connaissance plus approfondie du phénomène RMN.

Certains gaz comme le xénon peuvent aussi être mesurés lorsqu'ils sont adsorbés dans des matériaux poreux par exemple.

Historique

La spectroscopie RMN est née en 1946 lorsque Felix Bloch et Edward Mills Purcell, de manière indépendante, réalisèrent les premières mesures du magnétisme nucléaire par induction magnétique. Ils ont reçu pour cette invention le prix Nobel de physique en 1952^[1]. Les développements ont été ensuite conséquents: En 1950, Erwin L. Hahn découvre les échos de spin à la base des nombreuses techniques multi-impulsionnelles utilisées de nos jours^[2]. La même année, W. Proctor et W. Dickinson découvrent indépendamment le phénomène de déplacement chimique, découverte fondamentale pour l'essor des applications de la RMN en chimie organique^[3],[4]. En 1959, E.R. Andrew démontre que la rotation d'un échantillon autour d'un axe particulier, l'angle magique, permet l'obtention de spectres résolus en RMN des solides (RMN MAS)^[5]. Enfin, une étape majeure dans le développement de la mesure du phénomène RMN est la conception de la spectroscopie RMN par transformée de Fourier par Richard R. Ernst en 1966. Il a reçu le prix Nobel de chimie en 1991 pour cette découverte et les développements de la RMN multidimensionnelle que cette technique a permis^[6].

Principes de base

La spectroscopie RMN repose sur la détection du phénomène RMN, qui se produit lorsque des noyaux atomiques de spin non nuls sont placés dans un champ magnétique externe généralement uniforme et qu'ils sont excités par un rayonnement radiofréquence accordé sur les différences d'énergie entre les différents états possibles du spin nucléaire.

La fréquence de résonance ν₀ (appelée fréquence de Larmor) est en première approximation directement proportionnelle au champ appliqué B₀:

ν₀ = γB₀

où γ = 2πγ est le rapport gyromagnétique (ou magnétogyrique).

Le fait que chaque isotope possède un rapport gyromagnétique unique permet à la technique RMN de pouvoir être réglée sur un élément particulier. Il suffit d'ajuster la fréquence d'excitation et d'observation sur le noyau ciblé.

La fréquence de résonance des noyaux dépend aussi de leur environnement, les spins étant en interaction avec celui-ci. Ces interactions sont appelées interactions internes par opposition aux interactions externes des spins avec le champ magnétique externe et le rayonnement radiofréquence. Ces interactions intra- ou intermoléculaires peuvent être magnétiques comme c'est le cas pour le déplacement chimique et les couplages dipolaires, encore ou électriques, ce qui est le cas de l'interaction quadripolaire. L'interprétation et la mesure de ces interactions permettent d'avoir des informations précieuses sur :

• la nature et le nombre d'atomes voisins des noyaux étudiés,
• la liaison chimique,
• la conformation moléculaire,
• les distances interatomiques,
• la mobilité moléculaire,
• etc.

Le déplacement chimique

Origine du déplacement chimique

Quand une molécule est placée dans le champ magnétique externe B₀, des champs magnétiques locaux sont créés par la circulation des électrons induite dans les diverses orbitales moléculaires sous l'action du champ. Ces champs locaux vont la plupart du temps s’opposer proportionnellement à l’action du champ magnétique B₀. Le champ réellement « ressenti » localement par les noyaux n'est donc plus exactement le champ appliqué, mais se trouve diminué. Cet effet s'appelle le diamagnétisme en physique (appelé parfois « blindage » dans le cas de la RMN)

D'autres effets peuvent intervenir qui sont également susceptibles de modifier le champ local, comme le paramagnétisme électronique, lorsqu’il y a des électrons délocalisés (noyaux aromatiques, liaisons chimiques fortement polarisées, électrons non appariés…) ou non appariés qui vont au contraire augmenter le champ ressenti par les noyaux. C'est alors un effet paramagnétique (appelé parfois « déblindage » dans le cas de la RMN).

La façon dont la fréquence de résonance de chaque noyau est affectée par ces champs locaux est caractérisée par une constante d'écran, σ, qui contient les contributions dia- et paramagnétiques :

ν_L = ν₀(1 − σ)

La différence de fréquence δ induite par les différents environnements électroniques est généralement appelée déplacement chimique, et il est pratique de la définir par rapport à une référence arbitraire et de l'exprimer en ppm en utilisant la relation suivante :

La référence choisie dépend de l'isotope étudié. Par exemple pour le ¹H, ¹³C et ²⁹Si, le tétraméthylsilane (ou TMS) est choisi en général.

Le tableau suivant présente les références utilisées pour d'autres noyaux^[7].

Les interactions dipolaires magnétiques

Représentation de l'interaction magnétique dipôle-dipôle ou couplage dipolaire pour une paire de spins nucléaires.

Représentation de l'interaction de couplage scalaire

Les interactions dipolaires magnétiques entre deux spins couplés donnent lieu à une variation d'énergie de leurs états quantiques respectifs, et par conséquent modifient leurs résonances.

Cette interaction peut exister soit directement à travers l'espace (couplage dipolaire direct), soit par l'intermédiaire des électrons situés dans les orbitales moléculaires de liaison (appelé couplage dipolaire indirect, scalaire ou encore couplage J)^[8].

Les couplages dipolaires directs

Le couplage dipolaire direct dépend de la distance r_ij entre deux noyaux i et j en interaction et de leurs rapports gyromagnétiques, γ_i et γ_j.

L'intensité du couplage (souvent appelée constante dipolaire) peut être définie (en Hz) par :

où μ0 est la perméabilité magnétique du vide.

Par exemple, deux protons séparés de 20Å présentent une constante dipolaire de -15kHz^[9].

Le déplacement des niveaux d'énergie produit un éclatement dipolaire, c'est-à-dire l'apparition d'un doublet à la place d'une résonance unique pour chacun des spins. La valeur de l'éclatement est donnée par :

Δν_ij = kD_ij(3cos ²β_ij − 1)

où β_ij est l'orientation du vecteur internucléaire ,c'est-à-dire reliant les deux noyaux, par rapport au champ appliqué B₀.

k vaut 3/2 si les deux noyaux sont identiques, par exemple deux protons (couplage homo-nucléaire). Il vaut 1 dans le cas de deux noyaux différents (couplage hétéro-nucléaire).

Si les réorientations moléculaires sont très rapides comme dans les liquides, l'éclatement disparait, car la moyenne s'annule.

Dans les solides, la mesure de l'interaction dipolaire est un moyen puissant d'obtenir les distances interatomiques^[10].

Les couplages dipolaires indirects ou scalaires

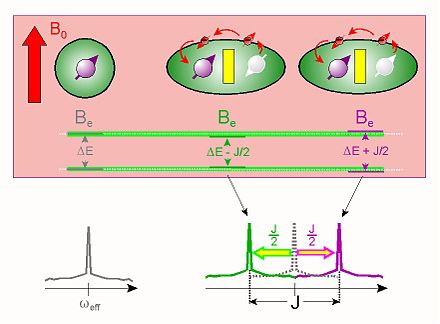
Les couplages dipolaires directs (à travers l'espace) sont annulés dans les liquides, mais lorsqu'une liaison chimique existe les spins sont tous de même couplés via les électrons^[11]. Ce couplage indirect qui résiste aux réorientations moléculaires est donc souvent appelé couplage scalaire(c'est-à-dire indépendant de l'orientation). Il se nomme aussi couplage « J » en spectroscopie RMN en référence à la constante J_ij qui en définit l'intensité.

Le couplage dipolaire scalaire est un excellent indicateur de la présence de liaison chimique et une aide précieuse dans la détermination des structures de molécules organiques.

L'interaction quadripolaire

L'interaction quadripolaire^[12] ne concerne que les isotopes atomiques de spin égal ou supérieur à 1. Ceux-ci représentent environ les 3/4 des isotopes observables en RMN, parmi lesquels des atomes très importants en chimie comme l'oxygène (¹⁷O), l'azote (¹⁴N), le Chlore(³⁵Cl,³⁵Cl)…

La principale caractéristique qui les distingue des noyaux de spin 1/2 comme l'hydrogène (¹H) ou le carbone (¹³C), c'est la présence d'un moment quadripolaire électrique^[13] en plus du moment magnétique nucléaire. Ce moment est dû à une distribution anisotrope des charges dans le noyau. Ce moment quadripolaire électrique est susceptible d'interagir avec tous gradients de champ électrique non nul au niveau du noyau. Cette interaction quadripolaire est susceptible de modifier très fortement l'énergie des états quantiques et donc influence la fréquence de résonance et la relaxation.

Les effets sur la fréquence de résonance disparaissent dans les liquides à cause des réorientations rapides des molécules. L'interaction quadripolaire devient nulle également si le noyau dans un solide est localisé dans un environnement très symétrique (symétrie sphérique du gradient de champ électrique).

L'anisotropie des interactions

Représentation du tenseur de constantes d'écran par un ellipsoïde

Dans la majeure partie des cas, les électrons n'ont pas une distribution sphérique autour du noyau. Cette distribution dépend beaucoup de la géométrie de la molécule, il en résulte que les interactions internes sont en général anisotropes.

Dans les solutions liquides, ce n'est pas important, car on n'observe qu'une valeur moyenne à cause des rapides réorientations moléculaires (mouvement brownien). Dans les solides par contre, la position des raies de résonance est alors fortement modifiée suivant l'orientation de la molécule, du cristal ou plus généralement de la cristallite.

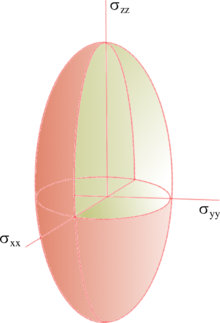
Dans le cas du déplacement chimique par exemple, la constante d'écran ne sera plus représentée par un simple scalaire σ, mais par un tenseur du second ordre, qui définit les composantes de la constante d'écran selon les différentes directions de l'espace. Il existe toujours trois directions particulières orthogonales, c'est-à-dire un système d'axes principaux, qui peuvent être choisies comme référentiel pour décrire l'interaction de telle sorte que le tenseur soit diagonal dans ce système d'axes. Ainsi :

Les trois scalaires σ_xx, σ_yy et σ_zz, correspondent à la valeur de la constante d'écran selon les trois directions principales. Ce tenseur peut se représenter sous forme d'un ellipsoïde dont la forme dépend de la symétrie de l'interaction. Notamment, si l'interaction est de symétrie axiale (σ_xx = σ_yy < σ_zz), l'ellipsoïde est un ellipsoïde de révolution. Si les trois valeurs sont égales, le système est isotrope et peut alors être décrit par une seule constante d'écran σ = σ_xx = σ_yy = σ_zz.

La fréquence de résonance de chaque noyau dépendra directement du tenseur d'écran et pourra s'écrire :

où les angles α et β sont les coordonnées angulaires sphériques donnant l'orientation de l'axe principal z par rapport au champ magnétique B₀, et ν₀ est la fréquence de Larmor, ν₀ = − γB₀

Les échantillons solides sont souvent analysés sous forme de poudre, c'est-à-dire qu'ils contiennent un ensemble de cristallite dont les orientations sont aléatoires. Le spectre de résonance observé correspondra alors à la superposition des résonances de toutes les cristallites présentes. Un tel spectre est appelé spectre de poudre et présente des formes caractéristiques de la symétrie du tenseur d'écran.

L'anisotropie de déplacement chimique est en général désignée par l'acronyme anglais CSA (pour chemical shift anisotropy).

L'interaction dipolaire est aussi anisotrope dans les solides, mais a la particularité d'être de symétrie axiale.

Séquences d'impulsion

relaxation: La relaxation (généralement exponentielle) longitudinale (le long de l'axe z est décrite par une constante de temps appelée T₁, celle dans le plan x-y est décrite par la constante de temps T₂

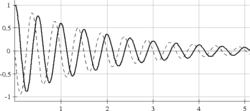
La technique la plus simple pour obtenir un spectre RMN consiste en l'application d'une impulsion de champ radiofréquence optimisée. Cette impulsion a une durée permettant d'obtenir le signal maximum dans la bobine de détection. Ceci est obtenu lorsque la direction de l'aimantation nucléaire est amenée dans le plan perpendiculaire au champ B₀. A la suite de cette impulsion, le signal est mesuré tandis qu'il diminue du fait de la relaxation. Deux types de relaxation peuvent être différentiés. L'un, la relaxation T₂ représente la décroissance de l'aimantation dans le plan perpendiculaire à B₀, tandis que l'autre, la relaxation T₁, représente le recouvrement de l'aimantation le long de B₀ (voir figure ci-contre).

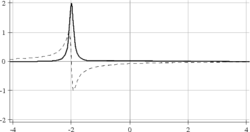
Le signal mesuré est souvent appelé FID (d'après l'anglais Free Induction Decay) et se présente comme une sinusoïde ou une superposition de sinusoïdes selon qu'il y a une ou plusieurs résonances présentes dans le spectre RMN. Afin de connaître le signe de la fréquence de résonance, il est nécessaire de faire une détection synchrone en quadrature, c'est-à-dire la mesure de deux signaux décalés temporellement d'un quart de période de Larmor (traits plein et pointillé sur la figure ci-dessous).

Une transformée de Fourier de ce signal mesuré produit un spectre RMN en fréquence.

La décroissance apparente du FID est due à la relaxation T₂, mais aussi à des effets expérimentaux liés par exemple à inhomogénéité des champs magnétiques utilisés et aux différences de susceptibilités magnétiques internes à l'échantillon. Ceci fait que la relaxation apparente est souvent plus rapide que la relaxation physique des spins. La constante de temps décrivant cette décroissance sera plutôt nommée T pour la différencier du « vrai » T₂. Plus la constante T est faible, plus le FID est court et plus le signal transformé en fréquence est large. C'est donc un facteur important dans la résolution spectrale: Il est primordial de préparer des échantillons les plus homogènes possible et d'utiliser des aimants pour produire le champ magnétique externe les plus homogènes et stables possible. La géométrie de la bobine utilisée pour produire les impulsions de champs radiofréquence est aussi d'une importance cruciale.

Si la séquence d'impulsion la plus simple se résume à une seule impulsion suivie de la mesure du FID résultant, la spectroscopie RMN moderne fait aussi largement appel à des séquences d'impulsions beaucoup plus sophistiquées, c'est-à-dire des enchainements d'impulsions qui permettent une manipulation à volonté des spins nucléaires. Une extension importante de ces séquences d'impulsion est la spectroscopie 2D (à deux dimensions) et même nD (multidimensionnelle) qui permettent en particulier d'établir des corrélations entre différentes résonances.

Écho de spin

Mesure de la relaxation

Transfert de polarisation

RMN à deux dimensions (2D)

Principe

COSY

RMN multiquanta

Mesure de distance

La RMN en chimie organique

L'échantillon est préparé puis placé dans un tube en verre (Tube RMN).

La spectroscopie RMN est un des outils d'analyse les plus utilisés en chimie organique.^{[réf. souhaitée]}

Les noyaux les plus souvent étudiés sont l'¹H, le ¹³C, le ³¹P et le ¹⁹F de spin nucléaire égal à 1/2. Sont étudiés également l'¹⁷O de spin 5/2 et Le ¹⁴N de spin 1.

L'échantillon à analyser est généralement mis en solution dans un solvant, souvent du chloroforme deutéré, (CDCl₃).^{[réf. souhaitée]} Ce solvant est 100% enrichi en Deuterium (²D, un isotope de l'¹H) afin qu'il soit invisible en RMN du proton. Le deutérium a effectivement une fréquence de résonance bien différente de celle de l'hydrogène, son rapport gyromagnétique valant 6,54 au lieu de 42,58 MHz/T pour l'hydrogène.

La réalisation d'un spectre RMN du ¹H est généralement rapide (quelques minutes d'acquisition). Grâce à l'analyse des déplacements chimiques de chaque résonance et de leur structure fine (multiplet) due aux couplages scalaires, il est possible de déterminer la structure de beaucoup de molécules organiques. Cette détermination est facilitée en utilisant aussi en parallèle la spectroscopie RMN du ¹³. L'acquisition d'un spectre est cependant plus longue compte tenu de l'abondance naturelle très faible de cet isotope du carbone (~ 1.1%).

Les techniques de spectroscopie RMN multidimensionnelle sont utilisées pour faciliter l'interprétation de spectres complexes.

L'interprétation des spectres RMN simples

spectre RMN ¹H de l'éthanol

L'analyse d'un spectre RMN fait appel à trois opérations:

• L'attribution des résonances en fonction des déplacements chimiques (détermination des groupes fonctionnels)
• L'intégration des différentes résonances ou groupes de résonances (détermination de la proportion de chaque groupe)
• La détermination de la multiplicité du signal et éventuellement des constantes de couplages (détermination du nombre de voisins de chaque noyau / détermination de la structure)

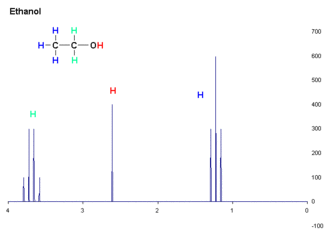
La détermination du déplacement chimique permet de déduire une grande partie des informations structurales sur la molécule étudiée. Par exemple, le spectre RMN de l'éthanol (CH₃CH₂OH), montre trois groupes de signaux spécifiques à trois déplacements chimiques différents (3,8, 2,6 et 1,3 ppm). La comparaison de ces déplacements avec des tables de déplacements chimiques^{[14][réf. insuffisante]} que les trois groupes peuvent être attribué aux groupes CH₂, OH et CH₃, respectivement.

L'analyse de l'aire des différents groupes permet de confirmer cette attribution, puisqu'ils sont approximativement dans le rapport 2:1:3. les logiciels d'analyse moderne ^{[réf. souhaitée]} permettent l'intégration des différentes résonances, mais ce paramètre doit être utilisé avec précaution, car de nombreux paramètres peuvent influencer sur l'intensité des résonances surtout dans les expériences complexes faisant intervenir plusieurs impulsions.

Une des informations les plus utiles en spectroscopie RMN pour la détermination de la structure de molécules organiques vient du couplage scalaire (ou couplage J, un cas particulier du couplage dipolaire) entre noyaux de spin non nul. Ce couplage résulte de l'interaction de différents états de spin à travers les liaisons chimiques d'une molécule. Il s'accompagne de l'éclatement signaux de RMN en multiplets dépendant du nombre de voisins (de spin non nul). Ce couplage fournit un aperçu détaillé de la connectivité des atomes dans une molécule.

L'analyse des multiplets peut être parfois simple, notamment si les couplages sont du premier ordre):

• Si un noyau est couplé à n noyaux de spin 1/2, sa résonance se divise en un multiplet composé de n + 1 avec des ratios d'intensité qui peuvent être déterminé assez souvent suivant le triangle de Pascal:
• S’il y a d'autres couplages avec des noyaux non équivalents aux premiers, cela amènera d'autres séparations. Si le couplage a lieu entre des noyaux qui sont chimiquement équivalents (c'est-à-dire qui ont le même déplacement chimique), cela n'a pas d'effet sur les spectres RMN.

Par exemple, dans le spectre de protons de l'éthanol, le groupe CH₃ est divisé en un triplet avec un rapport d'intensité de 1:2:1 par les deux voisins protons CH₂. De même, le CH₂ est divisé en un quartet avec un ratio d'intensité de 1:3:3:1 par les trois voisins protons CH₃. En principe, les deux protons CH₂ devraient être également divisée à nouveau en un doublet pour former un doublet de quartets à cause du couplage avec le proton hydroxyle, mais l'échange intermoléculaire du proton hydroxyle acide entraîne l'annulation de ce couplage.^{[réf. souhaitée]}

La description ci-dessus suppose que la constante de couplage est faible en comparaison avec la différence de fréquences de déplacement chimique entre les spins non équivalents. Sinon, les intensités des multiplets sont modifiées et donc moins faciles à analyser (surtout si plus de deux spins sont impliqués)^{[réf. souhaitée]}.

Spectroscopie RMN de corrélation

La spectroscopie de corrélation est un type de spectroscopie 2D (bidimensionnelle) ou parfois nD (multidimensionnelle). Ce type de technique RMN est souvent désigné par son acronym COSY (en)^{[réf. souhaitée]}. Les autres types de spectroscopie 2D sont par exemple, la spectroscopie J-résolue (J-resolved)^{[réf. souhaitée]}, la spectroscopie d'échange (EXSY)^{[réf. souhaitée]}, la spectroscopie d’effet Overhauser (NOESY (en))^{[réf. souhaitée]}, les spectroscopies hétéronucléaires (qui concernent 2 isotopes différents) tel que HSQC (en)^{[réf. souhaitée]}, HMQC (en)^{[réf. souhaitée]} et HMBC (en)^{[réf. souhaitée]}.

Les spectres à deux dimensions (2D) donnent plus informations que les spectres classiques à une dimension et sont particulièrement utiles pour déterminer la structure d'une molécule, particulièrement celles qui sont trop complexes à étudier à l'aide la spectroscopie 1D.^{[réf. souhaitée]}

La RMN en biologie structurale

À côté de la radiocristallographie, la RMN est devenue une méthode d'étude des macromolécules biologiques en solution. Elle ne nécessite pas l'obtention de monocristaux et permet d'étudier des protéines, des acides nucléiques à des concentrations millimolaires. Les techniques de RMN multidimensionnelles conduisent à corréler les fréquences de plusieurs spins et de résoudre les ambiguïtés liées aux superpositions spectrales. Des protéines de masse moléculaire de 10 à 30 kDa peuvent être analysées ainsi que des oligonucléotides de plusieurs dizaines de paires de bases.

RMN homonucléaire sans marquage isotopique

Historiquement, les protéines ont été étudiées par la RMN du proton (isotope ¹H) présent en abondance.

Une première étape consiste à attribuer les résonances, c'est-à-dire à établir une corrélation entre les signaux du spectre et les atomes d'hydrogène de la molécule. Deux expériences clefs sont utilisées, l'expérience de corrélation par les couplages scalaires (HOHAHA ou TOCSY) et l'expérience de corrélation à travers l'espace par effet Overhauser (NOESY). Cette attribution est dite séquentielle, car elle opère par positionnement relatif d'un noyau par rapport à ses voisins en utilisant l'information de la séquence peptidique. Ce processus d'attribution (semblable à un puzzle) devient de plus en plus complexe à mesure que la taille de la protéine augmente; de plus, l'effet Overhauser se transmet à travers l'espace et ne permet pas de distinguer des noyaux proches dans la séquence peptidique et ceux proches dans l'espace. Des erreurs sont donc possibles qui ne se détectent qu'à la fin du processus, lorsque certaines pièces du puzzle restent sur le tapis.

Une fois les spectres attribués, les informations sont alors utilisées de manière quantitative : les couplages scalaires renseignent sur les angles dièdres et les effets Overhauser sur des distances interatomiques (jusqu'à 4-6 angströms). Ces informations sont introduites dans des programmes de modélisation moléculaire, pour rechercher une ou plusieurs conformations de la molécule compatibles avec les données. La stratégie est comparable à celle du géomètre qui mesure des distances et des angles entre bâtiments et recalcule un plan de ville. Sauf que la portée des distances mesurées en RMN est faible par rapport aux objets évalués; l'accumulation des erreurs expérimentales et/ou le faible nombre de données conduisent à des structures localement mal définies.

Deux difficultés limitent la taille des macromolécules accessibles à la technique : la complexité des spectres et la largeur individuelle de chaque signal. Si la taille de la protéine double, le nombre de résonances du spectre va doubler sans que la dispersion (c'est-à-dire la largeur spectrale) n'augmente. Une solution consiste à recourir à un spectromètre RMN à plus haut champ et donc beaucoup plus coûteux. Si la taille double, la masse moléculaire augmente et la protéine tourne plus lentement sur elle-même par mouvement diffusif. Cela conduit à des signaux plus larges, car la relaxation transversale devient plus performante. L'augmentation du champ magnétique est sans effet et il faut trouver une autre parade au problème (réduction de la viscosité, réduction du nombre de protons voisins…).

RMN hétéronucléaire avec marquage isotopique

Afin de résoudre les superpositions spectrales dans les grosses molécules, il s'avérait nécessaire de passer de la RMN 2D à la RMN 3D. Des essais peu fructueux ont été faits au début des années 1990 pour combiner les séquences HOHAHA et NOESY dans une expérience tridimensionnelle. Si on dispose d'une protéine entièrement enrichie en ¹⁵N et en ¹³C, on peut concevoir des expériences de corrélation entre spins, uniquement fondées sur des couplages scalaires et permettant de relier tout le squelette peptidique ainsi que les chaînes latérales. Les isotopes naturellement abondants sont respectivement le ¹⁴N (noyau quadripolaire) et le ¹²C (noyau invisible en RMN), mais la plupart des protéines étant obtenues par surexpression bactérienne, il est possible de faire des cultures sur des milieux enrichis isotopiquement.

Cette nouvelle stratégie fait appel à une série d'expériences 3D triple résonance: 3D car un spectre tridimensionnel est obtenu, triple résonance car les fréquences de trois noyaux différents sont détectées. Pour des raisons de sensibilité, toutes ces séquences partent du ¹H (noyau au rapport gyromagnétique élevé) et se terminent par la détection du même noyau. Dans l'expérience HNCO, on établit donc une corrélation entre le proton amide (^HN), son azote (N) et le carbonyle (CO) de l'acide aminé précédent. Les couplages scalaires utilisés pour les transferts de cohérence sont des couplages ¹J (à une liaison) et donc relativement importants (¹JNH = 90 Hz et ¹JNCO=15Hz). Cela assure donc une grande efficacité de transfert même dans le cas de protéines de masse élevées (largeur de raie). À noter que cette expérience HNCO permet de relier par couplage scalaire des acides aminés, ce que la stratégie homonucléaire ne permettait pas (absence de couplage scalaire 3J à travers la liaison peptidique)

La RMN des solides

La rotation à l'angle magique

Principe de la rotation à l'angle magique (MAS) d'un échantillon solide

Dans les liquides, les mouvements browniens entrainent des réorientations très rapides de molécules, de sorte que seule la moyenne des interactions prise sur l'ensemble des orientations est mesurée. Dans les solides, ce n'est pas le cas puisque les mouvements des molécules sont souvent beaucoup plus lents que la mesure du signal RMN. Les spectres de poudres sont parfois très larges si le milieu est très anisotrope; les spectres se superposent et la séparation d'espèces chimiques différentes en fonction de leur déplacement chimique par exemple n'est donc pas aussi facile que dans les liquides.

Dans les années 1960, Andrew^[15] a montré cependant qu'il était possible d'obtenir des spectres correspondant à la moyenne isotrope des interactions en faisant tourner l'échantillon autour d'un axe incliné de θ = 54.74° par rapport au champ magnétique. Cet angle est appelé, l’angle magique, et la technique de rotation à l'angle magique est en général désignée par son acronyme anglais: MAS (pour magic angle spinning)

Une condition essentielle pour que cette technique MAS soit réellement efficace est que la vitesse de rotation soit au moins de l'ordre de grandeur de l'amplitude de l'anisotropie. Ainsi pour moyenner efficacement l'interaction dipolaire entre un atome de ¹³C et un proton, la vitesse ou plutôt la fréquence de rotation doit être de l'ordre de 30 kHz (c'est-à-dire 30000 tours par seconde). Ce sont des vitesses très importantes qui ne peuvent être obtenues qu'en plaçant l'échantillon dans de petits conteneurs cylindriques (le rotor) placés en rotation dans une turbine à coussins d'air. Les vitesses actuellement atteintes avec ces systèmes avoisinent les 90 kHz.

Applications en sciences des matériaux

Polymères

Solides cristallins

Verres

Matériaux poreux

Autres applications

Notes et références

Notes

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « NMR_spectroscopy » (voir la liste des auteurs)

Références

Bibliographie

Ouvrages de base recommandés

• (en) M. H. Levitt, Spin Dynamics: Basics of Nuclear Magnetic Resonance, Wiley, 2008, 2^e éd. (ISBN 9780470511176) 
• Daniel Canet, Le RMN : concepts et méthodes, Paris, Interéditions, 1991 (ISBN 978-2-7296-0375-5) 
• (en) James Keeler, Understanding NMR Spectroscopy, Chichester, Wiley, 2010, poche (ISBN 978-0-470-01787-6) (LCCN 2005022612) 

Autres Ouvrages

Généraux

• (en) A. Abragam, The Principles of Nuclear Magnetism, Oxford, Oxford University Press, 1994, reprint^e éd., poche (ISBN 978-0-19-852014-6) (LCCN 61002889) , La « bible » (difficile)
• (en) C. P. Slichter, Principles of Magnetic Resonance (Springer Series in Solid-State Sciences), Berlin, Springer, 1989, 3^e éd. (ISBN 978-3-540-50157-2) 
• (en) M. Mehring, Principles of High Resolution Nmr in Solids, Berlin, Springer-Verlag, 1983, 2 Rev Enl^e éd. (ISBN 978-0-387-11852-9) (LCCN 82010827) 
• (en) Richard R. Ernst, Geoffrey Bodenhausen, Alexander Wokaun, Principles of Nuclear Magnetic Resonance in One and Two Dimensions, Oxford, Oxford University Press, USA, 1990, poche (ISBN 978-0-19-855647-3) (LCCN 85026014) 
• (en) Eiichi Fukushima, Stephen B.w. Roeder, Experimental Pulse NMR: A Nuts and Bolts Approach, Reading, Westview Press, 1993, 7^e éd., poche (ISBN 978-0-201-62726-8) (LCCN 81007901) 

RMN en chimie organique

• (en) Harald Günther, NMR Spectroscopy: Basic Principles, Concepts, and Applications in Chemistry, 2nd Edition, Chichester, Wiley, 1995, 2^e éd., poche (ISBN 978-0-471-95201-5) (LCCN 94023084) 

RMN en Biochimie

• (en) John Cavanagh, Wayne J. Fairbrother, Arthur G. Palmer III, Nicholas J. Skelton, Mark Rance, Protein NMR Spectroscopy, Second Edition: Principles and Practice, Amsterdam, Academic Press, 2006, 2^e éd. (ISBN 978-0-12-164491-8) (LCCN 2006021096) 
• (en) Gordon S. Rule, T. Kevin Hitchens, Fundamentals of Protein NMR Spectroscopy, Dordrecht, Springer, 2005, 1^re éd. (ISBN 978-1-4020-3499-2) (LCCN 2008447860) 

RMN du solide

• (en) Melinda J. Duer, Introduction to Solid-State NMR Spectroscopy, Malden, Wiley-Blackwell, 2005, 1^re éd., poche (ISBN 978-1-4051-0914-7) (LCCN 2003063027) 
• (en) Robin K. Harris, Roderick E. Wasylishen, Melinda J. Duer, NMR Crystallography, Chichester, Wiley, 2010, First Edition^e éd. (ISBN 978-0-470-69961-4) (LCCN 2009031427) 
• (en) Klaus Schmidt-Rohr, Hans Wolfgang Spiess, Multidimensional Solid-State NMR and Polymers, London, Academic Press, 1994 (ISBN 978-0-12-626630-6) 

Encyclopédies

(en) Encyclopedia of Nuclear Magnetic Resonance, eds. D.M. Grant, R. K. Harris (ISBN 0470847840) 

Voir aussi

Articles connexes

• Résonance magnétique nucléaire
• Imagerie par résonance magnétique

Liens externes

• (en) Recommendations IUPAC 1997
• (en) NMR Wiki (Open NMR project), un wiki consacré à la RMN

• Portail de la physique
• Portail de la chimie