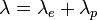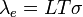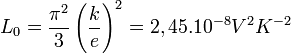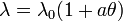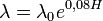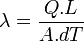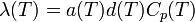- Watt par mètre-kelvin
-
Conductivité thermique
La conductivité thermique est une grandeur physique caractérisant le comportement des matériaux lors du transfert thermique par conduction. Cette constante apparaît par exemple dans la loi de Fourier (voir l’article Conduction thermique). Elle représente la quantité de chaleur transférée par unité de surface et par une unité de temps sous un gradient de température.
Sommaire
Généralités
Dans le système international d’unités, la conductivité thermique est exprimée en watts par mètre par kelvin, (W·m-1·K-1) où :
- le watt est l’unité de puissance
- le mètre est l’unité de longueur
- le kelvin est l’unité de température
La conductivité dépend principalement de :
-
- La nature du matériau,
- la température.
- D’autres paramètres comme l’humidité, la pression interviennent également.
En général, la conductivité thermique va de pair avec la conductivité électrique. Par exemple, les métaux, bons conducteurs d'électricité sont aussi de bons conducteurs thermiques. Il y a des exceptions, la plus exceptionnelle est celle du diamant qui a une conductivité thermique élevée, entre 1000 et 2600 W·m-1·K-1, alors que sa conductivité électrique est basse.
D’un point de vue atomique, la conductivité thermique est liée à deux types de comportements :
-
- le mouvement des porteurs de charges, électrons ou trous.
- l’oscillation des atomes autour de leur position d’équilibre.
Dans les métaux, le mouvement des électrons libres est prépondérant alors que dans le cas des non-métaux, la vibration des ions est la plus importante.
La conductivité thermique est donc liée d’une part à la conductivité électrique (mouvement des porteurs de charge) et d'autre part à la structure même du matériau (vibrations des atomes). En effet dans un solide, les vibrations des atomes ne sont pas aléatoires et indépendantes les unes des autres, mais correspondent à des modes propres de vibration, aussi appelés « phonons » (on peut faire par exemple l’analogie avec un pendule ou une corde de guitare, dont la fréquence de vibration est fixée. Ces modes propres de vibration correspondent à des ondes qui peuvent se propager dans le matériau, si sa structure est périodique (organisée). Cette contribution sera donc plus importante dans un cristal, ordonné, que dans un verre, désordonné (d’où par exemple la différence de conductivité thermique entre le diamant ci-dessus et le verre dans le tableau).
Mathématiquement, la conductivité thermique λ peut donc s'écrire comme la somme de deux contributions :
où
-
- λe est la contribution des porteurs de charge (électrons ou trous)
- λp est la contribution des vibrations des atomes (phonons)
La contribution des porteurs de charge est liée à la conductivité électrique σ du matériau par la relation de Wiedemann-Franz :
où L est appelé « Facteur de Lorentz ». Ce nombre L dépend des processus de diffusion des porteurs de charge (ce qui correspond plus ou moins à la façon dont ils sont gênés par des obstacles lors de leurs déplacements, voir aussi diffusion des ondes) ainsi que de la position du niveau de Fermi. Dans les métaux, il est égal au nombre de Lorentz L0, avec :
où
-
- k est la constante de Boltzmann
- e est la charge de l'électron
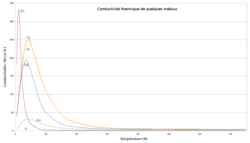
Ordres de grandeur des conductivités thermiques de quelques matériaux
Matériaux Conductivité thermique
(W·m-1·K-1)
Valeurs pour une température de 20 °CAcier doux 46 Acier inoxydable (18% Chrome, 8% Nickel) 26 Adobe (terre crue) 0,32 Air (100 kPa) 0,0262 Aluminium (pureté de 99,9%) 237 Al-SiC 150-200 Amiante 0,168 Ardoise (parallèle) 2,50 à 95°C[1] Ardoise (perpendiculaire) 1,4 à 95°C[1] Argent 418[2] Asphalte (2,1 g/cm³) 0,06[1] Bakélite (1,3 g/cm³) 1,4[1] Basalte 2[1] Béton 0,92[2] Bois de chêne 0,16[1] Bois de noyer (0,65 g/cm³) 0,14[1] Bois de pin (parallèle aux fibres) 0,36 Bois de pin (perpendiculaire aux fibres) 0,15 Brique (terre cuite) 0,84[2] Caoutchouc vulcanisé (EPDM) 0,36 à 0,40 Calcaire (2 g/cm³) 1[1] Carbone 129 Carton Charbon de bois (0,2 g/cm³) 0,055[1] Contreplaqué 0,11[1] Craie 0,92[1] Cuivre 390[2] Diamant 1000-2600 Dihydrogène (gaz) 0,18 Dioxygène (gaz) 0,027 Eau 0,6[2] Epoxy 0,25 Étain 66,6 Fer 80[3] Fonte 100 Granite (2,8 g/cm³) 2,2[1] Grès (2,2 g/cm³) 1,3[1] Hélium (gaz) 0,14[3] Houille (1,35 g/cm³) 0,26[1] Laine 0,05 Laine de roche (150 à 175 kg/m³) 0,045[4] Laine de verre 0,04[2] Liège 0,04[2] Marbre 0,30[2] Mortier de chaux 0,87 Mousse de Polyuréthane rigide 0,025 Or 317 Ouate de cellulose 0,041 Paille (perpendiculaire aux fibres) 0,04 perlite 0,038 Platine 71,6 Plomb 35[3] Polystyrène expansé 0,036 Pouzzolane Quartz 6,8-12 Roseau (en panneau) 0,056 Schiste Silicium 149 Nitrure de silicium (Sialon) 20-65 Terre (sèche) 0,75 Titane 20 Verre 1,2[2] Zinc 116 Si le diamant a une conductivité thermique très élevée, celle du diamant bleu naturel l’est encore plus. On peut donc examiner des gemmes pour déterminer si elles sont de véritables diamants en utilisant un appareil de contrôle de la conductivité thermique, un des instruments standard utilisé en gemmologie. Les diamants de n'importe quelle taille paraissent toujours très froids au toucher en raison de leur effusivité thermique élevée.
À densité et humidité égales, le bois résineux est plus conducteur que le bois feuillu. Plus un bois est dense et plus il est humide, plus il est conducteur.
Évolution avec la température
La conductivité thermique évolue avec la température.
Pour les solides, elle répond à la loi suivante :
où
-
- λ0 est la conductivité thermique du matériau à 0 K
- a est un coefficient caractéristique de chaque matériau
- θ est la température en Kelvin
a est positif pour les isolants thermiques et négatif pour les conducteurs thermiques.
Quand la température augmente, un isolant perd de sa capacité d'isolation et inversement un conducteur perd de sa capacité de conduction.
ATTENTION: équation non valide pour les hautes températures
Évolution avec l'humidité
Pour les matériaux de construction, il est courant d’utiliser la relation suivante :
où
-
- λ0 est la conductivité thermique du matériau sec
- H est l’humidité relative en pourcentage.
- e représente la fonction exponentielle
Mesure de la conductivité thermique
Mesure à l'état stationnaire
Le principe de la détermination de la conductivité thermique d’un matériau repose sur le lien entre le flux de chaleur qui traverse ce matériau et le gradient de température qu’il génère. Il est illustré sur la figure suivante :
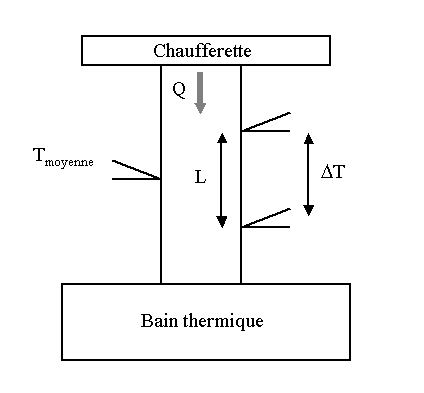
L’une des extrémités de l’échantillon de section A est fixée à un doigt froid (bain thermique) dont le rôle est d'évacuer le flux thermique traversant l'échantillon, et l’extrémité opposée à une chaufferette dissipant dans l’échantillon une puissance électrique Q obtenue par effet Joule, de manière à produire un gradient thermique suivant la longueur de l’échantillon. Des thermocouples séparés par une distance L mesurent la différence de température dT le long de l’échantillon. Un troisième thermocouple, calibré, est également fixé à l’échantillon pour déterminer sa température moyenne (la température de mesure). La conductivité thermique est alors donnée par :
Si dT n’est pas trop important (de l'ordre de 1 °C), la conductivité thermique mesurée est celle correspondant à la température moyenne mesurée par le troisième thermocouple. Le principe de la mesure repose alors sur l’hypothèse que la totalité du flux de chaleur passe par l’échantillon. La précision de la mesure dépend donc de la capacité à éliminer les pertes thermiques, que ce soit par conduction thermique par les fils, convection par le gaz résiduel, radiation par les surfaces de l’échantillon ou pertes dans la chaufferette : la mesure s'effectue donc dans des conditions adiabatiques. Pour assurer la meilleure précision possible, l’échantillon dont on souhaite mesurer la conductivité thermique est donc placé dans une chambre de mesure sous vide (pour minimiser la convection). Cette chambre est elle-même enveloppée dans plusieurs boucliers thermiques dont la température est régulée (afin de minimiser les effets radiatifs). Enfin, les fils des thermocouples sont choisis de manière à conduire le moins possible la chaleur.
Etant donné qu’il est d'autant plus difficile de minimiser les pertes thermiques que la température augmente, cette technique ne permet la mesure de la conductivité thermique qu’à des températures inférieures à la température ambiante (de 2 kelvins à 200 kelvins sans difficultés, et jusqu’à 300 kelvins (27 °C) pour les meilleurs appareils de mesure).
Mesure par la méthode dite « Laser Flash »
Pour les températures supérieures à la température ambiante, il devient de plus en plus difficile d’éliminer ou de tenir compte des pertes thermiques par radiation (conditions adiabatiques), et l’utilisation de la technique à l’état stationnaire présentée ci-dessus n’est pas recommandée. Une solution est de mesurer la diffusivité thermique en lieu et place de la conductivité thermique. Ces deux grandeurs sont en effet liées par la relation :
où
-
- λ(T) est la conductivité thermique en mW.cm-1.K-1
- a(T) est la diffusivité thermique en cm2.s-1
- d(T) est la masse spécifique en g.cm-3
- Cp(T) est la chaleur spécifique en J.g-1.K-1
Si l’on suppose que la masse spécifique ne varie pas avec la température, il suffit de mesurer la diffusivité thermique et la chaleur spécifique pour obtenir une mesure de la conductivité thermique à haute température.
La figure suivante schématise l’appareillage utilisé pour la mesure de conductivité thermique par la méthode dite « laser flash » :
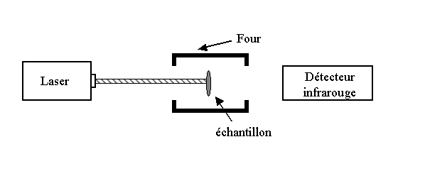
Un échantillon cylindrique dont l’épaisseur d est nettement plus faible que son diamètre est placé dans un porte-échantillon qui se trouve à l’intérieur d’un four maintenu à température constante. Une de ses faces est illuminée par des pulses (de l’ordre de la milliseconde) émis par un laser, ce qui assure un chauffage uniforme de la face avant. La température de la face arrière est mesurée, en fonction du temps, à l’aide d’un capteur de mesure infrarouge. En l’absence de pertes thermiques de l’échantillon, la température devrait augmenter de manière monotone. Dans une situation réelle, l’enregistreur mesurera un pic de température suivi d’un retour à la température du four. Le temps t nécessaire pour que la face arrière atteigne la moitié de la température de pic (par rapport à la température du four), permet de déterminer la diffusivité thermique suivant :
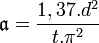
Il est alors possible de calculer la conductivité thermique grâce à la masse spécifique et la chaleur spécifique.
La difficulté de cette technique réside dans le choix des paramètres de mesure optimums (puissance du laser et épaisseur de l'échantillon).
Normes et règlements
En France, ont été promulguées des normes successives pour inciter les bâtisseurs à une isolation thermique maximale des bâtiments. Par exemple la norme RT 2000 puis la norme RT 2005.
Notes et références
- ↑ a , b , c , d , e , f , g , h , i , j , k , l , m et n Handbook of Chemistry & Physics
- ↑ a , b , c , d , e , f , g , h et i Thermodynamique, fondements et applications, J.Ph. Pérez, A.M. Romulus, p155 édition Masson
- ↑ a , b et c Harris Benson. Physique 1 : mécanique. 3e édition. Éditions du Renouveau Pédagogique, Saint-Laurent, Québec, 2004, p. 519.
- ↑ NBN B 62-002/A1"
Articles connexes
- Portail de la physique
Catégories : Grandeur physique | Propriété chimique | Transfert thermique | Science des matériaux
Wikimedia Foundation. 2010.