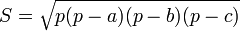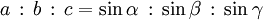Théorème du sinus

Loi des sinus

Fig. 1 - Notations usuelles dans un triangle quelconque.

En trigonométrie, la loi des sinus est une relation de proportionnalité entre les longueurs des côtés d'un triangle et les sinus des angles respectivement opposés.

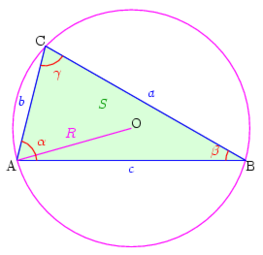
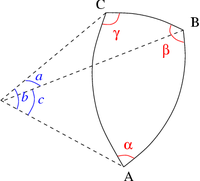
On considère un triangle quelconque ABC, représenté sur la Fig. 1 ci-contre, où les angles sont désignés par les minuscules grecques et les côtés opposés aux angles par la minuscule latine correspondante :

a = BC et α = angle formé par [AB] et [AC] ;
b = AC et β = angle formé par [BA] et [BC] ;
c = AB et γ = angle formé par [CA] et [CB].

Alors,

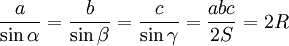$\,\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma} = \frac{abc}{2 S} = 2R$ ,

où R est le rayon du cercle circonscrit au triangle ABC et

$S = \sqrt{p(p-a)(p-b)(p-c)}$

est l'aire du triangle donnée à partir du demi-périmètre p par la formule de Héron.

La relation de proportionnalité est parfois résumée ainsi :

$\,a\,:\,b\,:\,c = \sin\alpha\,:\,\sin\beta\,:\,\sin\gamma$

Fig. 2 - Résolution d'un triangle par la loi des sinus

Le théorème peut être utilisé

pour déterminer le rayon du cercle circonscrit
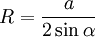
$\,R = \frac{a}{2\sin\alpha}$
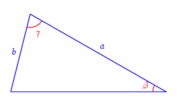
pour résoudre un triangle dont on connaît un angle, un côté adjacent à l'angle et un côté opposé (cf. Fig. 2 ci-contre)
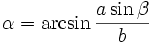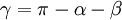$\alpha = \arcsin \frac{a\sin\beta}{b}$ et donc $\,\gamma = \pi - \alpha -\beta$ .

Sommaire

1 Généralisation aux géométries non euclidiennes
- 1.1 Géométrie sphérique
- 1.2 Géométrie hyperbolique
2 Généralisation à l'espace euclidien
3 Voir également
4 Bibliographie

Généralisation aux géométries non euclidiennes

Fig. 3 - Triangle sphérique : dimensions réduites a, b et c ; angles α, β et γ.

Pour une surface non euclidienne de courbure K, on note ρ le rayon de courbure. Il vérifie

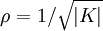$\,\rho = 1/\sqrt{|K|}$ .

On définit alors les dimensions réduites du triangle :

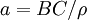$\,a = BC/\rho$ ,

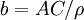$\,b = AC/\rho$ ,

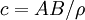$\,c = AB/\rho$ .

Dans le cas d'un triangle sphérique, a, b et c correspondent à la mesure angulaire des segments de grand arc [BC], [AC] et [AB] (voir Fig. 3).

Géométrie sphérique

Dans un triangle sphérique ABC dessiné sur la sphère de centre O et de rayon ρ (Fig. 3), la loi des sinus s'écrit

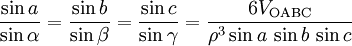$\frac{\sin a}{\sin\alpha} = \frac{\sin b}{\sin\beta} = \frac{\sin c}{\sin\gamma} = \frac{6 V_{\mathrm{OABC}}}{\rho^3\sin a\,\sin b\,\sin c}$ ,

où V_OABC est le volume du tétraèdre OABC.

Géométrie hyperbolique

Dans un triangle hyperbolique, la loi des sinus s'écrit

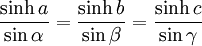$\frac{\sinh a}{\sin\alpha} = \frac{\sinh b}{\sin\beta} = \frac{\sinh c}{\sin\gamma}$ .

Généralisation à l'espace euclidien

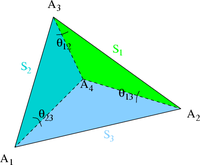
On considère un tétraèdre A₁A₂A₃A₄ de l'espace euclidien. La figure 3 ci-contre présente les notations concernant les sommets, faces et angles dans le tétraèdre :

Fig. 3 - Tétraèdre : faces et angles diédraux.

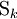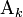$\,\mathrm S_k$ la face opposée opposée au sommet $\mathrm A_k\$ ;
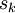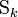$\,s_k$ la surface de $\mathrm S_k\$ ;
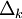$\,\Delta_k$ le plan dans lequel 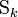$\mathrm S_k\$ est plongée ;
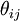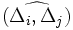$\,\theta_{ij}$ l'angle diédral $\widehat{(\Delta_i, \Delta_j)}$ .

On définit le sinus de l'angle triédral formé par les sommets $A 1$ , etc. comme suit

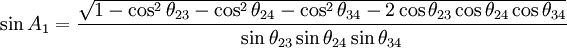$\sin A_1 = \frac{\sqrt{1-\cos^2\theta_{23}-\cos^2\theta_{24}-\cos^2\theta_{34}-2\cos\theta_{23}\cos\theta_{24}\cos\theta_{34} }}{\sin\theta_{23}\sin\theta_{24}\sin\theta_{34}}$ ;
etc.

Alors

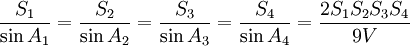$\frac{S_1}{\sin A_1} = \frac{S_2}{\sin A_2} = \frac{S_3}{\sin A_3} = \frac{S_4}{\sin A_4} = \frac{2S_1S_2S_3S_4}{9V}$ ,

où V est le volume du tétraèdre.

Voir également

Bibliographie

Loi des sinus sur le site Math World (en anglais)
Loi des sinus généralisée sr le site Math World (en anglais)

Portail de la géométrie

Ce document provient de « Loi des sinus ».

Catégories : Trigonométrie | Mathématiques élémentaires | Géométrie du triangle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème du sinus de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Theoreme d'Al-Kashi — Théorème d Al Kashi Fig. 1 Notations usuelles dans un triangle quelconque. Le théorème d Al Kashi, en France, ou loi des cosinus, dans les autres pays francophones et dans d autres langues, est un théorème de géométrie du triangle couramment… … Wikipédia en Français
Théorème d'Al-kashi — Fig. 1 Notations usuelles dans un triangle quelconque. Le théorème d Al Kashi, en France, ou loi des cosinus, dans les autres pays francophones et dans d autres langues, est un théorème de géométrie du triangle couramment utilisé en trigonométrie … Wikipédia en Français
Théorème d'Al Kashi — Fig. 1 Notations usuelles dans un triangle quelconque. Le théorème d Al Kashi, en France, ou loi des cosinus, dans les autres pays francophones et dans d autres langues, est un théorème de géométrie du triangle couramment utilisé en trigonométrie … Wikipédia en Français
Théorème d'al-kashi — Fig. 1 Notations usuelles dans un triangle quelconque. Le théorème d Al Kashi, en France, ou loi des cosinus, dans les autres pays francophones et dans d autres langues, est un théorème de géométrie du triangle couramment utilisé en trigonométrie … Wikipédia en Français
Théorème de Pythagore généralisé — Théorème d Al Kashi Fig. 1 Notations usuelles dans un triangle quelconque. Le théorème d Al Kashi, en France, ou loi des cosinus, dans les autres pays francophones et dans d autres langues, est un théorème de géométrie du triangle couramment… … Wikipédia en Français
Théorème du cosinus — Théorème d Al Kashi Fig. 1 Notations usuelles dans un triangle quelconque. Le théorème d Al Kashi, en France, ou loi des cosinus, dans les autres pays francophones et dans d autres langues, est un théorème de géométrie du triangle couramment… … Wikipédia en Français
Theoreme de Morley — Théorème de Morley Le théorème de Morley, découvert par Frank Morley en 1898, est un théorème de géométrie plane. Il s énonce comme suit : « Les intersections des trissectrices des angles d un triangle forment un triangle… … Wikipédia en Français
Théorème de morley — Le théorème de Morley, découvert par Frank Morley en 1898, est un théorème de géométrie plane. Il s énonce comme suit : « Les intersections des trissectrices des angles d un triangle forment un triangle équilatéral » Le triangle… … Wikipédia en Français
Théorème de Céva — Théorème de Ceva Pour les articles homonymes, voir Ceva (homonymie). Les droites (AD), (BE) et (CF) sont concourantes ou parallèles si et seulement si … Wikipédia en Français
Théorème de ceva — Pour les articles homonymes, voir Ceva (homonymie). Les droites (AD), (BE) et (CF) sont concourantes ou parallèles si et seulement si … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème du sinus

Loi des sinus

Sommaire