Théorème de Bernoulli

Pour les articles homonymes, voir Loi de Bernoulli.

Le théorème de Bernoulli qui a été établi en 1738 par Daniel Bernoulli exprime le bilan hydraulique simplifié d'un fluide dans une conduite. Il a posé les bases de l'hydrodynamique et, d'une façon plus générale, de la mécanique des fluides.

Formulation usuelle

Pour un écoulement^[1]

d'un fluide incompressible (on peut considérer que la masse volumique reste constante)
irrotationnel (le rotationnel de la vitesse du fluide est nul, ce qui traduit un écoulement non tourbillonnaire, ce qui revient à dire que le champ de vitesse dérive d'un potentiel) ou dans le cas d'un fluide dont le rotationnel n'est pas nul, si l'on se place le long d'une même ligne de courant.
d'un fluide parfait (les effets visqueux sont négligeables et pas de perte de charge)

Alors, en régime permanent, si l'on néglige les transferts de chaleur, on vérifie :

$\frac{v^2}{2 \cdot g} + z +\frac{p}{\rho \cdot g} = \mathrm{constante}$ ^[2]

où :

$p\,$ est la pression en un point (en Pa ou N/m²)

$\rho\,$ est la masse volumique en un point (en kg/m³)

$v\,$ est la vitesse du fluide en un point (en m/s)

$g\,$ est l'accélération de la pesanteur (en N/kg ou m/s²)

$z\,$ est l'altitude (en m)

La constante intervenant dans le second membre de l'équation n'est pas universelle mais propre à l'écoulement, il s'agit d'une constante le long d'une ligne de courant, appelée charge. Avec ce choix de normalisation, elle est homogène à une longueur.

Interprétation

Cette équation traduit en fait le bilan de l'énergie le long d'une ligne de courant :

$e_c = \tfrac1V \cdot \tfrac12 \cdot m \cdot v^2 = \tfrac12 \cdot \rho \cdot v^2$ est la densité volumique d'énergie cinétique (énergie cinétique par unité de volume, m étant la masse du volume V de fluide) ;
$e_z = \tfrac1V \cdot m \cdot g \cdot z = \rho \cdot g \cdot z$ est la densité volumique d'énergie potentielle de gravité ;
$e_p = \tfrac1V \cdot p \cdot V = p$ est la densité volumique d'énergie élastique.

La loi de bilan s'écrit donc

$e c + e z + e p = c o n s t a n t e$

ce qui amène à l'équation ci-dessus en divisant par ρ·g.

Formulations étendues

On trouve souvent d'autres formulations du théorème de Bernoulli dans des contextes plus généraux.

Pour des fluides compressibles :

Lorsque les effets de compressibilité dans un fluide ne sont plus négligeables (vitesse des particules de fluide comparable à la vitesse du son dans le fluide), il devient nécessaire d'apporter une correction au terme caractérisant l'énergie potentielle élastique du fluide, dans le cas idéal d'un gaz parfait on a :

$\frac {v^2}{2 \cdot g} + z +\left(\frac {\gamma}{\gamma-1}\right)\frac {p}{\rho \cdot g} = \mathrm{constante}$ ^[3]

où $\gamma\,$ est le rapport des capacités calorifiques du fluide : $\frac{C_{p}}{C_{v}}$ .

Formulation thermodynamique :

$\frac {v^2}{2 \cdot g} + z + \frac{h}{g} = \mathrm{constante}$ ^[4]

où $h$ désigne l'enthalpie spécifique (i.e. par unité de masse). $h=u+\frac{p}{\rho}$ , où $u$ désigne l'énergie interne spécifique du fluide.

échange d'énergie :

Dans le cas d'un écoulement d'un point A vers un point B avec échange d'énergie (présence d'une pompe ou d'une turbine), l'expression devient :

$\frac {1}{2} \rho \cdot v_A^2 + p_A + \rho \cdot g \cdot z_A +\frac {P}{Q_V} = \frac {1}{2} \rho \cdot v_B^2 + p_B + \rho \cdot g \cdot z_B$

$Q V$ représente le débit-volume du fluide (en m3/s)

$P$ représente la puissance (en watt) de la machine. $P$ > 0 dans le cas d'une pompe (la puissance est reçue par le fluide) et $P$ < 0 dans le cas d'une turbine (la puissance est fournie par le fluide).

Démonstrations

Équation de Bernoulli pour les fluides incompressibles

L'équation de Bernoulli pour les fluides incompressibles peut être démontrée par intégration des équations d'Euler du mouvement, qui dans les hypothèses du théorème se ramènent à l'équation de Navier-Stokes.

On peut également appliquer le principe de conservation de l'énergie le long d'une ligne de courant, en négligeant les effets thermiques, de viscosité, de compressibilité.

C'est ce second point de vue que l'on suit ici.

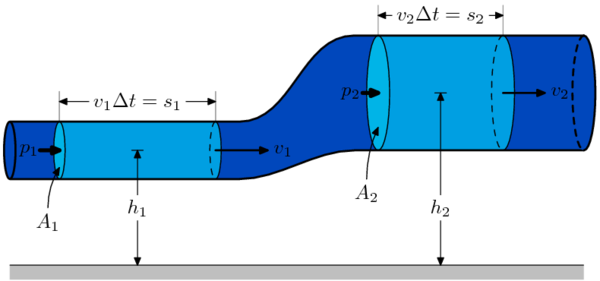
Tube de courant du fluide. On indique les pressions (p), altitudes (h), vitesses (v), longueurs (s) et sections (A).

Soit le système fermé contenu à l'instant $t$ entre $x 1$ et $x 2$ et à $t + Δ t$ entre $x 1 + v 1 .Δ t$ et $x 2 + v 2 .Δ t$ .

Le fluide est incompressible, la masse $Δ m$ contenue entre $x 1$ et $x 1 + v 1 .Δ t$ doit être identique à la masse contenue entre $x 2$ et $x 2 + v 2 .Δ t$ .

Ce que l'on peut ramener ici à la conservation du débit massique : $Δ t . v 1 . A 1 .ρ = Δ t . v 2 . A 2 .ρ$ .

Toutes les forces qui s'exercent (forces pressantes et poids) sont conservatives (il n'y a pas d'effet visqueux). On peut donc appliquer le théorème de conservation de l'énergie mécanique au système :

Δ E p p + Δ E k = W

où

$\Delta E_{k}=\Delta m(v^{2}_{2}- v^{2}_{1})/2$ est la variation d'énergie cinétique du système.

$Δ E p p = Δ m g h 2 - Δ m g h 1$ est la variation d'énergie potentielle de pesanteur du système.

$W = p 1 A 1 .(v 1 Δ t) - p 2 A 2 .(v 2 Δ t)$ est le travail des forces de pressions.

Soit :

$\frac{1}{2}\Delta mv_{2}^{2}- \frac{1}{2}\Delta mv_{1}^{2} + \Delta mgh_{2} -\Delta mgh_{1}= p_{1}A_{1}.(v_{1}\Delta t) - p_{2}A_{2}.(v_{2}\Delta t)$

D'où, en divisant par $Δ m$ :

$\frac{v_{1}^{2}}{2}+g h_{1}+\frac{p_{1}}{\rho}=\frac{v_{2}^{2}}{2}+g h_{2}+\frac{p_{2}}{\rho}$

Et donc :

$\frac{v^{2}}{2}+g h+\frac{p}{\rho}=C$

On peut remarquer que la démonstration est faite dans le contexte particulier d'un écoulement obéissant à la géométrie de la figure. Cependant, pour un écoulement quelconque en régime permanent, on pourra toujours définir au voisinage d'une ligne de courant une section sur laquelle la vitesse est homogène, et raisonner comme précédemment.

Équation de Bernoulli pour les fluides compressibles

La démonstration est identique à celles pour les fluides incompressibles : elle s'appuie sur la conservation du débit et de l'énergie.

Mais on doit prendre en compte dans la variation d'énergie du système la variation d'énergie interne du fluide entre $t$ et $t + Δ t$ .

La conservation de l'énergie appliquée au système devient alors :

$\frac{1}{2}\Delta mv_{2}^{2}- \frac{1}{2}\Delta mv_{1}^{2} + \Delta mgh_{2} -\Delta mgh_{1} + \Delta mu_{2} - \Delta mu_{1} = p_{1}A_{1}.(v_{1}\Delta t) - p_{2}A_{2}.(v_{2}\Delta t)$

D'où :

$\frac{v_{1}^{2}}{2}+g h_{1}+ u_{1} + \frac{p_{1}}{\rho}=\frac{v_{2}^{2}}{2}+g h_{2}+ u_{2}+\frac{p_{2}}{\rho}$

Si on note l'enthalpie spécifique $ω$ , dans le cas d'un gaz parfait, on vérifie $\gamma = \frac{\omega}{u}$ .

Comme $\omega = u + \frac{p}{\rho}$ , on a $\omega = \frac{\gamma}{\gamma -1}.\frac{p}{\rho}$

Donc dans ce cas,

$\frac{v^{2}}{2}+g h+ \frac{\gamma}{\gamma -1}.\frac{p}{\rho}= constante$

Applications

À vitesse nulle (v = 0), on retrouve la loi de la statique des fluides.

Effet Venturi :

Supposons maintenant que la vitesse ne soit pas nulle, mais que l'on reste toujours à la même altitude (z constant).

Si un liquide s'écoule dans une canalisation, alors comme il est incompressible, son débit (volume transitant à travers une surface par unité de temps) est constant. Si la canalisation s'élargit, alors la vitesse diminue (puisque le débit est le produit de la vitesse par la section, les deux varient à l'inverse). Le théorème de Bernoulli nous indique alors que la pression augmente. À l'inverse, si la canalisation se rétrécit, le fluide accélère et sa pression diminue. On qualifie ce dispositif expérimental de tube de Venturi.

Ce résultat est assez peu intuitif car on s'attendrait à ce que la pression augmente lorsque la section diminue.

Effet Magnus :

Si maintenant la conduite reste de section constante mais que l'on met un obstacle à l'intérieur ; l'obstacle diminue la section, on a donc le même effet. Si cet obstacle est un cylindre tournant, d'axe perpendiculaire à l'axe de la canalisation, alors le frottement accélère le fluide d'un côté et le ralentit de l'autre. On a donc une diminution de pression d'un côté et une augmentation de l'autre, le cylindre subit une force : c'est l'effet Magnus (l'on considère souvent l'effet Magnus dans l'air, qui est un fluide compressible, mais le principe général reste le même).

Si la canalisation a une section constante, et qu'elle ne présente pas d'obstacle, alors la vitesse est constante. Si l'altitude varie, alors l'équation de Bernoulli nous indique que la pression varie à l'opposé de l'altitude.

On peut évaluer alors la pression dynamique : $q = \tfrac12 \cdot \rho \cdot v^2$

Tube de Pitot :

Cet appareil de mesure permet d'évaluer la vitesse d'écoulement d'un fluide en mesurant la différence de pression entre deux points A et B de l'écoulement joint par une ligne de courant. Au point A, le fluide est supposé être à vitesse (quasi) nulle, on cherche la vitesse en B. Les points étant sensiblement à la même altitude, on peut appliquer le théorème de Bernoulli sous sa forme usuelle entre A et B.

Approche historique

La première formulation du théorème de Bernoulli apparaît dans Hydrodynamica - De viribus et motibus fluidorum commentarii de Daniel Bernoulli (première édition en 1738)^[5] . Pour d'Alembert, ce texte est l'œuvre fondatrice de l'hydrodynamique en tant que discipline physique moderne^[6].

Il est alors formulé comme un bilan macroscopique global et une méthode de calcul, dans le cadre de la résolution d'un problème technique : la détermination de la durée de vidange des vases munis d'un orifice.

La justification réside dans l'égalité de la montée potentielle et de la descente actuelle^[7]. Il s'agit d'une transposition aux fluides de la conservation des forces vives, déjà connue en mécanique, et qui est en fait l'ancêtre du principe de conservation de l'énergie dans le domaine de la physique classique.

C'est seulement en 1755, avec les travaux d'Euler^[8], que le théorème apparaît sous la forme d'un bilan local plus proche des formulations contemporaines.

Voir aussi

Notes et références

↑ (fr)Mécanique des fluides sur www.ac-nancy-metz.fr. Consulté le 3 octobre 2010.
↑ Bruhat, G., Mécanique, 6^e édition, Masson, 1967
↑ Clancy, L.J., Aerodynamics, Section 3.11, Pitman Publishing, London, 1975
↑ Van Wylen, G.J., and Sonntag, R.E., Fundamentals of Classical Thermodynamics, Section 5.9, John Wiley and Sons Inc., New York, 1965
↑ Service Commun de la Documentation - Patrimoine numérisé
↑ Jean Le Rond d'Alembert, article Hydrodynamique de l'Encyclopédie (Tome VIII), 1765 [1]
↑ traduction de Jean Peyroux, 2004
↑ Leonhard Euler, Principes Généraux du mouvement des fluides, 1755 [2]

v · Mécanique des fluides
Fluides	Fluide caloporteur • Fluide de Stokes • Fluide hydraulique • Fluide incompressible • Fluide parfait • Fluide électrorhéologique
Écoulements	Écoulement complexe • Écoulement de Couette • Écoulement de Poiseuille • Écoulement incompressible • Écoulement laminaire • Écoulement torrentiel • Écoulement polyphasique
Équations	Équations de Navier-Stokes • Théorème de Bernoulli •Équation de Darcy-Weisbach • Équation de Prony • Équation de Rankine-Hugoniot • Équation de Schlichting • Écoulement de Stokes • Équations d'Euler • Équation de continuité • Équations primitives atmosphériques
Nombres	Nombre d'Archimède • Nombre capillaire • Nombre d'Ekman • Nombre d'Ellis • Nombre de Bond • Nombre de Bulygin • Nombre de Cameron • Nombre de Fedorov • Nombre de Froude • Nombre de Galilée • Nombre de Grashof • Nombre de Goucher • Nombre de Hartmann • Nombre de Hedström • Nombre de Hersey • Nombre de Karlovitz • Nombre de Kutateladze • Nombre de Lewis • Nombre de Mach • Nombre d'Ohnesorge • Nombre de Prandtl • Nombre de Rayleigh • Nombre de Reech • Nombre de Reynolds • Nombre de Rossby • Nombre de Rouse • Nombre de Schmidt • Nombre de Stewart • Nombre de Strouhal • Nombre de Taylor • Nombre de Weber

Portail de la physique

Catégories :

Mécanique des fluides
Théorème de physique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Bernoulli de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Theoreme de Bernoulli — Théorème de Bernoulli Pour les articles homonymes, voir Loi de Bernoulli. Le théorème de Bernoulli qui a été établi en 1738 par Daniel Bernoulli exprime le bilan hydraulique simplifié d un fluide dans une conduite. Il a posé les bases de l… … Wikipédia en Français
Théorème de bernoulli — Pour les articles homonymes, voir Loi de Bernoulli. Le théorème de Bernoulli qui a été établi en 1738 par Daniel Bernoulli exprime le bilan hydraulique simplifié d un fluide dans une conduite. Il a posé les bases de l hydrodynamique et, d une… … Wikipédia en Français
théorème de Bernoulli — ● théorème de Bernoulli Théorème dû à Daniel Bernoulli et exprimant la conservation de l énergie mécanique dans l écoulement d un fluide incompressible parfait … Encyclopédie Universelle
Theoreme de Kutta-Jukowski — Théorème de Kutta Jukowski Le théorème de Kutta Jukowski est un théorème fondamental d aérodynamique qui concerne la portance d un profil d aile . C est le fruit de la recherche au début du vingtième siècle de deux aérodynamiciens, Martin Wilhelm … Wikipédia en Français
Théorème de Kutta-Joukowsky — Théorème de Kutta Jukowski Le théorème de Kutta Jukowski est un théorème fondamental d aérodynamique qui concerne la portance d un profil d aile . C est le fruit de la recherche au début du vingtième siècle de deux aérodynamiciens, Martin Wilhelm … Wikipédia en Français
Théorème de kutta-jukowski — Le théorème de Kutta Jukowski est un théorème fondamental d aérodynamique qui concerne la portance d un profil d aile . C est le fruit de la recherche au début du vingtième siècle de deux aérodynamiciens, Martin Wilhelm Kutta, allemand, et… … Wikipédia en Français
Théorème de Kutta-Jukowski — Le théorème de Kutta Jukowski, théorème fondamental d aérodynamique, est le fruit de la recherche au début du XXe siècle de deux aérodynamiciens, Martin Wilhelm Kutta, allemand, et Nikolaï Joukovski (ou Jukowski ou Zhukovsky), russe. En… … Wikipédia en Français
Bernoulli — Famille Bernoulli Les Bernoulli qui se sont illustrés dans les mathématiques et la physique, sont issus de Nicolas Bernoulli (1623 1708), descendant d une famille ayant émigré d Anvers à Bâle à la fin du XVIe siècle. Les représentants les… … Wikipédia en Français
Theoreme isoperimetrique — Théorème isopérimétrique En géométrie, un théorème isopérimétrique traite d une question concernant les compacts d un espace métrique muni d une mesure. Un exemple simple est donné par les compacts d un plan euclidien. Les compacts concernés sont … Wikipédia en Français
Theoreme de Weierstrass-Casorati — Théorème de Weierstrass Casorati En mathématiques, et plus particulièrement en analyse complexe, le théorème de Weierstrass Casorati décrit une propriété topologique des voisinages d une singularité essentielle d une fonction holomorphe. Il est… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de Bernoulli

Sommaire

Formulation usuelle

Interprétation

Formulations étendues

Démonstrations

Applications

Approche historique

Voir aussi

Articles connexes

Notes et références

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Théorème de Bernoulli

Sommaire

Formulation usuelle

Interprétation

Formulations étendues

Démonstrations

Applications

Approche historique

Voir aussi

Articles connexes

Notes et références

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link