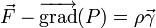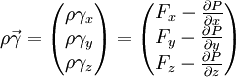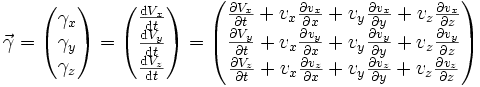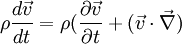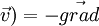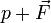Equations d'Euler
- Equations d'Euler
-
Équations d'Euler
L'équation d'Euler (établie par Euler en 1755) s'applique dans le cas d'un fluide parfait, c’est-à-dire un fluide non visqueux et sans conductivité thermique. Le fluide peut être incompressible ou compressible. Complétée par d'autres équations tirées de la dynamique des fluides parfaits, elle permet de caractériser un mouvement du fluide en calculant par exemple sa pression motrice.
Une intégration le long d'une ligne de courant de cette équation permet d'obtenir l'équation de Bernoulli.
L'équation d'Euler dérive de la relation fondamentale de la dynamique, appliquée à une particule fluide :
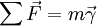
Faisons le bilan des forces appliquées à un élément de volume :
- les forces de volume
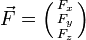 , proportionnelles à l'élement de volume considéré ;
, proportionnelles à l'élement de volume considéré ;
- les forces de pression, proportionnelles à l'élement de surface considéré ;
- les forces d'inertie, proportionnelles à l'accélération
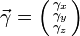 et au volume du fluide ;
et au volume du fluide ;
on obtient donc :
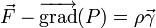
C'est la forme condensée de l'équation d'Euler.
En développant, on a :
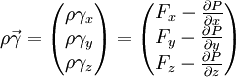
Une autre forme de l'équation d'Euler (les équations, dans ce cas) s'écrit :
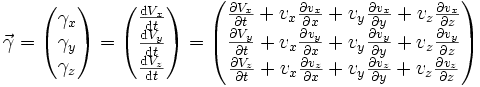
c'est à dire, 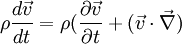
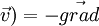
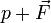
 Portail de la physique
Portail de la physique
Catégorie : Mécanique des fluides
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Equations d'Euler de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Équations d'Euler — Ne pas confondre avec l équation d Euler pour un polyèdre et diverses autres équations nommées d après Euler. L équation d Euler (établie par Leonhard Euler en 1755) s applique dans le cas d un fluide parfait, c’est à dire un fluide non… … Wikipédia en Français
Équations d'Euler-Lagrange — Équation d Euler Lagrange Pour les articles homonymes, voir Lagrange. L’équation d Euler Lagrange est un résultat mathématique qui joue un rôle fondamental dans le calcul des variations. On retrouve cette équation dans de nombreux problèmes réels … Wikipédia en Français
Euler — Leonhard Euler « Euler » redirige ici. Pour les autres significations, voir Euler (homonymie). Leonhard Euler … Wikipédia en Français
Équations de Navier-Stokes — Pour les articles homonymes, voir Stokes. En mécanique des fluides, les équations de Navier Stokes sont des équations aux dérivées partielles non linéaires qui décrivent le mouvement des fluides « newtoniens » (visqueux) dans… … Wikipédia en Français
Équations primitives atmosphériques — Les équations primitives atmosphériques sont une version simplifiée des équations de Navier Stokes. Elles sont applicables dans le cas d’un fluide à la surface d’une sphère en posant comme hypothèses que la composante verticale du mouvement est… … Wikipédia en Français
Équations de Hamilton-Jacobi — En mécanique hamiltonienne, les équations de Hamilton Jacobi sont des équations associées à une transformation du hamiltonien dans l espace des phases, et qui permettent de simplifier la résolution des équations du mouvement. Sommaire 1… … Wikipédia en Français
EULER (L.) — Avec Joseph Louis Lagrange, son émule plus jeune, Leonhard Euler est l’un des deux géants mathématiques qui ont dominé la science du XVIIIe siècle. Ses travaux, d’une abondance inégalée, couvrent tout le champ des mathématiques, de la mécanique… … Encyclopédie Universelle
Euler–Mascheroni constant — Euler s constant redirects here. For the base of the natural logarithm, e ≈ 2.718..., see e (mathematical constant). The area of the blue region is equal to the Euler–Mascheroni constant. List of numbers – Irrational and suspected irrational… … Wikipedia
ÉQUATIONS ALGÉBRIQUES — Dès la plus haute antiquité, on rencontre, à l’occasion de problèmes concrets, des exemples de résolution d’équations du premier et du second degré, et, jusqu’au début du XIXe siècle, l’étude des équations constitue l’unique préoccupation des… … Encyclopédie Universelle
Equations de Navier-Stokes — Équations de Navier Stokes Pour les articles homonymes, voir Stokes. En mécanique des fluides, les équations de Navier Stokes sont des équations aux dérivées partielles non linéaires qui décrivent le mouvement des fluides dans l approximation des … Wikipédia en Français
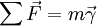
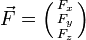 , proportionnelles à l'élement de volume considéré ;
, proportionnelles à l'élement de volume considéré ;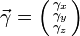 et au volume du fluide ;
et au volume du fluide ;