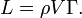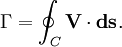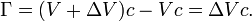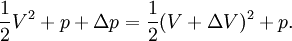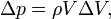- Théorème de Kutta-Joukowsky
-
Théorème de Kutta-Jukowski
Le théorème de Kutta-Jukowski est un théorème fondamental d'aérodynamique qui concerne la portance d'un profil d'aile . C'est le fruit de la recherche au début du vingtième siècle de deux aérodynamiciens, Martin Wilhelm Kutta, allemand, et Nikolaï Joukovski (ou Jukowski ou Zhukovsky), russe.
En introduisant la notion de circulation il permet d'échapper au paradoxe de d'Alembert selon lequel la force s'exerçant sur un corps quelconque en mouvement à vitesse constante sur une trajectoire rectiligne dans un fluide incompressible et parfait est égale à zéro.
Sommaire
Expression du théorème
Le théorème est généralement utilisé pour calculer la portance par unité d'envergure
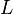d'un cylindre à section circulaire ou d'un profil d'aile d'envergure infinie. La formule fait intervenir la vitesse relative du cylindre 
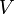, la masse volumique du fluide 
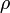et la circulation 
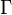:La circulation se calcule comme l'intégrale curviligne de la vitesse du fluide le long d'une courbe fermée entourant le cylindre :
Elle peut s'interpréter comme l'effet d'un tourbillon d'axe situé dans le profil.
Argument heuristique
Ce résultat se démontre rigoureusement mais il peut être approché par le raisonnement simplifié qui suit. Si l'incidence de l'écoulement par rapport au profil d'aile de corde
est telle que la vitesse soit 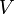sur l'extrados et 
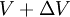sur l'intrados, la circulation peut se calculer commeLa différence de pression
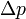entre les deux côtés se déduit du théorème de Bernoulli :En négligeant le second ordre,
ce qui conduit à la formule annoncée.
Condition de Kutta
Cette condition, parfois appelée condition de Joukowski, détermine la circulation autour d'un profil d'aile et permet donc d'en déduire sa portance.
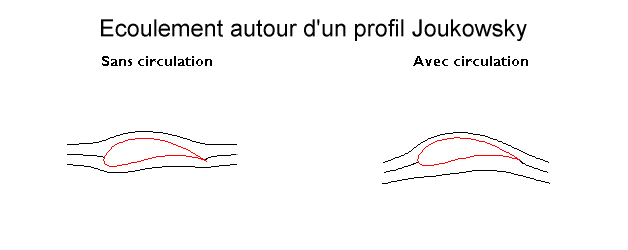
Quand un corps symétrique à forme lisse, comme un cylindre à section ovale, se déplace dans un fluide avec une incidence positive il y a deux points d'arrêt sur une section du corps, près du bord d'attaque sur l'intrados et du bord de fuite sur l'extrados. La circulation est nulle et il n'y a pas de portance.
Si un profil avec un bord de fuite aigu démarre avec une incidence positive, les deux points d'arrêt se trouvent au début dans les mêmes positions que précédemment. Quand l'air qui passe sous l'intrados atteint le bord de fuite il doit contourner celui-ci pour aller vers le point d'arrêt supérieur. À cause du rayon de courbure nul, la vitesse devrait être localement infinie. À défaut de vitesse infinie, il y a une vitesse importante qui crée sur l'extrados, près du bord de fuite, un tourbillon appelé tourbillon initiateur (starting vortex en anglais).
La circulation de ce tourbillon est équilibrée par celle du tourbillon attaché au profil. Lorsque la première croît, la seconde croît dans les mêmes proportions, ce qui déplace le tourbillon initiateur vers le bord de fuite où il quitte le profil avant d'être dissipé par viscosité. À ce stade, le positionnement du point d'arrêt au bord de fuite, qui constitue la condition de Kutta, a stabilisé l'écoulement.
La circulation restante autour du profil se traduit alors par des vitesses plus élevées (donc des pressions plus faibles selon le théorème de Bernoulli) sur l'extrados que sur l'intrados, donc par une portance calculable par le théorème de Kutta-Jukowski.
Cette portance est intimement liée au caractère anguleux du bord de fuite qui présente par ailleurs des inconvénients en termes de fabrication et de résistance.
Le schéma ci-après illustre, dans le cas d'un profil Joukowski, la création de la circulation, donc de la portance.
Voir aussi
Portail de la physique
Catégories : Aérodynamique | Théorème de physique
Wikimedia Foundation. 2010.
