- Théorie des groupes
-
La théorie des groupes est une discipline mathématique, c'est la partie de l'algèbre générale qui étudie les groupes, des structures algébriques. Le développement de la théorie des groupes est issu de la théorie des nombres, de la théorie des équations algébriques et de la géométrie.
Sommaire
Histoire
L'une des origines de l'idée de groupe est l'étude des équations algébriques par Joseph-Louis Lagrange (1771). La terminologie de « groupe » est mise en évidence pour la première fois par Évariste Galois (1830), qu'il rédigea la nuit précédant son duel : on peut « grouper » les automorphismes du corps de décomposition d'un polynôme séparable. L'idée de groupe tient aussi ses sources de l'étude de nouvelles géométries, Felix Klein (1872), et de la théorie des nombres : Leonhard Euler, Carl Friedrich Gauss.
Applications
La théorie des groupes est très utilisée en chimie. Elle sert par exemple à simplifier l'écriture de l'hamiltonien d'une molécule en exploitant ses symétries. Elle permet de calculer les orbitales moléculaires comme somme d'orbitales atomiques et de prédire le type de déformation que va subir une molécule en spectroscopie infrarouge (IR). En spectroscopie, elle permet de savoir si une transitions sera visible dans un spectre infrarouge et/ou dans un spectre Raman, selon la symétrie de sa déformation.
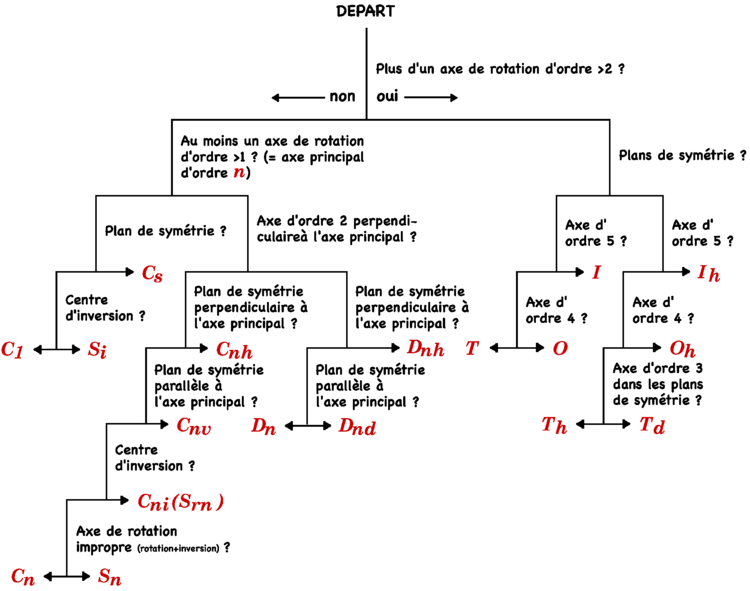
Chaque molécule possède une symétrie qui peut être déterminée à l'aide du synoptique dans la boîte déroulante ci-dessous. Une fois le groupe ponctuel de symétrie trouvé, on utilise la table de caractères correspondante[1].
Pour déterminer le groupe de symétrie d'une molécule
Dans les structures élémentaires de la parenté l’ethnologue Claude Lévi-Strauss, aidé du mathématicien André Weil, dégage le concept de structure élémentaire de parenté en utilisant la notion de groupe (en particulier le groupe de Klein)[2].
La théorie des groupes est aussi très utilisée en physique théorique, notamment pour le développement des théories de jauge.
Notes et références
- Tables de caractères des principaux groupes ponctuels de symétrie sur scienceamusante.net
- Paul Jolissaint Notes de lecture : Groupes et ethnologie
Articles connexes
Wikimedia Foundation. 2010.
