Théorèmes d'isomorphisme

Théorèmes d'isomorphisme

En mathématiques, les trois théorèmes d'isomorphisme fournissent l'existence d'isomorphismes dans le cadre de la théorie des groupes.

Ces trois théorèmes d'isomorphisme sont généralisables à d'autres structures que les groupes. Voir notamment à Algèbre universelle.

Sommaire

Premier théorème d'isomorphisme

Le premier théorème d'isomorphisme affirme qu'étant donné un morphisme de groupes f:G\to G', on peut rendre f injectif en quotientant G par son noyau.

Intuitivement, quotienter un groupe G par un sous-groupe H revient à « annuler » les éléments de H. En quotientant par le noyau de f, on fait donc en sorte que f(x) = 1 ne soit vrai que pour x = 1, ce qui est équivalent à l'injectivité de f.

Pour pouvoir parler de morphisme de groupes G/\operatorname{Ker} f\to G', il faut d'abord s'assurer que le quotient est muni d'une structure de groupe.

Proposition —  Soient G et G' deux groupes et soit f:G\rightarrow G' un morphisme de groupes. Alors \operatorname{Ker} f est un sous-groupe normal de G.

Démonstration

Notons \cdot les lois de G et G', ainsi que e et e' leurs éléments neutres, et vérifions que \operatorname{Ker} f est stable par conjugaison, c'est-à-dire que x\cdot h\cdot x^{-1}\in\operatorname{Ker} f pour tout x\in G et tout h\in\operatorname{Ker} f.

On a f(x\cdot h\cdot x^{-1}) = f(x)\cdot f(h)\cdot f(x^{-1}). Comme h est dans \operatorname{Ker} f, c'est-à-dire que f(h) = e', on en déduit que f(x\cdot h\cdot x^{-1}) = f(x)\cdot f(x^{-1}) = f(x\cdot x^{-1}) = f(e) = e'. Ainsi, x\cdot h\cdot x^{-1} est dans \operatorname{Ker} f et \operatorname{Ker} f est donc un sous-groupe normal de G.

Le fait que \operatorname{Ker} f soit un sous-groupe normal de G permet de définir sur le groupe quotient G / \operatorname{Ker} f une loi de groupe compatible avec celle de G. Grâce à cette compatibilité, le morphisme de groupes f : G \rightarrow G' induit un morphisme \widehat f : G / \operatorname{Ker} f \rightarrow \operatorname{Im} f.

On peut maintenant énoncer le théorème.

Premier théorème d'isomorphisme —  Soient G et G' deux groupes, et soit f:G \rightarrow G' un morphisme de groupes. Alors f induit un isomorphisme de G/\operatorname{Ker} f vers f(G).

Démonstration

Notons H le noyau de f. On définit \hat f en posant

\widehat f(xH) = f(x).
  • La fonction \widehat f est bien définie, c'est-à-dire que \widehat f(xH) ne dépend que de la classe xH et pas du représentant particulier x.

En effet, si y\in G est un autre représentant de xH, c'est-à-dire si xH = yH, alors xy^{-1}\in H=\operatorname{Ker} f donc f(x) = f(y), d'où \widehat f(xH)=\widehat f(yH).

  • Par définition de la loi de groupe quotient, \widehat f est un morphisme de groupes.
  • Le morphisme \widehat f est surjectif :

pour tout y\in f(G), il existe x\in G tel que f(x) = y ; mais alors \widehat f(xH)=f(x)=y.

  • Le morphisme \widehat f est injectif.

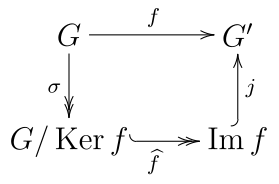
En effet, soit xH un élément de son noyau. Alors e'=\widehat f(xH)=f(x), c'est-à-dire que x est dans le noyau H de f. Mais alors xH = H, qui est l'élément neutre de G / H.

Une autre formulation possible du théorème précédent est que le morphisme f se factorise par la surjection et l'injection canoniques, c'est-à-dire que le diagramme qui suit est commutatif.

Diagramme commutatif de la factorisation canonique d'un homomorphisme
Factorisation d'un morphisme

Deuxième théorème d'isomorphisme

Deuxième théorème d'isomorphisme —  Soient G un groupe, N un sous-groupe normal de G et H un sous-groupe de G. Alors N \cap H est un sous-groupe normal de H, et on a l'isomorphisme suivant :

H/(H\cap N)\simeq HN/N.
Démonstration
  • Pour pouvoir parler du groupe HN / N, il faut d'abord montrer que HN est un groupe et que N en est un sous-groupe normal.

Soient hn et h'n' deux éléments de HN. On a hnh'n' = hh'(h' − 1nh')n', avec hh'\in H, h'^{-1}nh'\in N (puisque N est normal dans G) et n'\in N, donc hnh'n' est dans HN, ce qui montre que HN est stable par multiplication. On démontre facilement qu'il est stable par inverses, et non vide.

D'autre part, on a les inclusions de groupes N\subset HN\subset G, et N est normal dans G, donc il est également normal dans HN.

  • Pour établir l'isomorphisme, nous allons utiliser le premier théorème d'isomorphisme.

On dispose d'un morphisme injectif j:H\hookrightarrow HN définie par j(h) = h, et de la surjection canonique \sigma:HN\twoheadrightarrow HN/N (l'ensemble à l'arrivée est un groupe, puisque N est normal dans G). En composant ces deux morphismes, on obtient un nouveau morphisme f=\sigma\circ j:H\to HN/N défini par f(h) = hN.

  • Le morphisme f est surjectif.

En effet, soit (hn)N\in HN/N, avec h\in H et n\in N. Puisque n est dans N, hnN = hN, donc hnN = f(h).

  • Le noyau de f est H\cap N.

En effet, f(h) = hN est l'élément neutre N de HN / N si, et seulement si, h est dans N. Comme h est déjà dans H, cela revient à dire que h est dans N\cap H.

  • Le premier théorème d'isomorphisme assure alors que N\cap H est un sous-groupe normal de H, et que le morphisme induit \widehat f:H/(N\cap H)\to HN/N est un isomorphisme.

La conclusion de ce théorème reste vraie si l'on suppose seulement que le normalisateur de N contient H (au lieu de le supposer égal à G tout entier).


Troisième théorème d'isomorphisme

Troisième théorème d'isomorphisme — Soient G un groupe et N et M deux sous-groupes normaux de G tels que M soit inclus dans N. Alors N / M est un sous-groupe normal de G / M et on a l'isomorphisme suivant :

(G/M)/(N/M)\simeq G/N.
Démonstration

Le morphisme

G/M\to G/N,~gM\mapsto(gM)N=g(MN)=gN

est surjectif et de noyau N / M.

Voir aussi

Théorème de factorisation.

Référence

Serge Lang, Algèbre [détail des éditions] chapitre I, § 4


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorèmes d'isomorphisme de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Théorèmes d'isomorphismes — Théorèmes d isomorphisme En mathématiques, les trois théorèmes d isomorphisme fournissent l existence d isomorphismes dans le cadre de la théorie des groupes. Ces trois théorèmes d isomorphisme sont généralisables à d autres structures que les… …   Wikipédia en Français

  • Isomorphisme — Pour l isomorphisme en chimie, voir Isomorphisme (chimie). Pour l isomorphisme institutionnel, voir Isomorphisme institutionnel. En mathématiques, un isomorphisme entre deux ensembles structurés est une application bijective qui préserve la… …   Wikipédia en Français

  • Theoremes de Sylow — Théorèmes de Sylow En théorie des groupes, les théorèmes de Sylow forment une réciproque partielle du théorème de Lagrange, d après lequel, si H est sous groupe d un groupe fini G, alors l ordre de H divise l ordre de G. Un théorème de Sylow… …   Wikipédia en Français

  • Théorèmes de sylow — En théorie des groupes, les théorèmes de Sylow forment une réciproque partielle du théorème de Lagrange, d après lequel, si H est sous groupe d un groupe fini G, alors l ordre de H divise l ordre de G. Un théorème de Sylow garantit, pour certains …   Wikipédia en Français

  • Théorème d'isomorphisme — Théorèmes d isomorphisme En mathématiques, les trois théorèmes d isomorphisme fournissent l existence d isomorphismes dans le cadre de la théorie des groupes. Ces trois théorèmes d isomorphisme sont généralisables à d autres structures que les… …   Wikipédia en Français

  • Théorèmes de Sylow — Pour les articles homonymes, voir Sylow. En théorie des groupes finis, les théorèmes de Sylow forment une réciproque partielle du théorème de Lagrange, d après lequel, si H est sous groupe d un groupe fini G, alors l ordre de H divise l ordre de… …   Wikipédia en Français

  • Isomorphisme de Curry-Howard — Correspondance de Curry Howard La correspondance de Curry Howard, appelée[1] également correspondance preuve/programme ou correspondance formule/type, est une série de résultats à la frontière entre la logique mathématique, l informatique… …   Wikipédia en Français

  • Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”