Auto-régulation

Un système qui ne pourrait régler son propre fonctionnement en permanence est exposé à des risques d’emballement ou au contraire d’étouffement. C’est pourquoi dans la plupart des systèmes ayant une certaine pérennité on observe un ou plusieurs mécanismes, parfois spontanés, d'autorégulation, c’est-à-dire de régulation assurée par le système lui-même. Ces mécanismes sont étudiés par la cybernétique.

C’est dans certains cas le fait qu’ils possèdent cette autorégulation qui leur donne une stabilité suffisante pour qu’on ait l’occasion de les observer. C’est le cas par exemple des phénomènes de trombe, tornade, cyclone, et vraisemblablement de la grande tache rouge de Jupiter.

Sommaire 1 Trois exemples typiques 1.1 La neige 1.2 Les solutions tamponnées en chimie 1.3 Autorégulation dans le monde vivant 2 Autorégulation physique 2.1 Thermostat 2.2 Régulateur à boules de James Watt 2.3 Autorégulation du Soleil 3 Autorégulation en chimie 3.1 Principe de Le Châtelier 3.2 Loi d’action de masse et effet tampon 4 Autorégulation en biologie (cas d’un seul organisme, par opposition aux populations) 4.1 Glycémie 4.2 Système hormonal 4.3 Neurotransmetteurs 4.4 Système immunitaire 4.5 Expression / promotion / inhibition et autres régulations des gènes 5 Autorégulation et économie 5.1 La monnaie 5.2 Autorégulation du niveau de concurrence 5.2.1 Dans le cas du monopole (concurrence des divers emplois de la monnaie pour le consommateur) 5.2.2 Dans le cas de l’oligopole (pression bien plus forte à la baisse des coûts) 5.3 La « main invisible » d’Adam Smith 5.4 Autres aspects de l’autorégulation en économie 5.5 Limitations structurelles de l’autorégulation 6 Autorégulation et politique 7 Autorégulation des microsociétés 7.1 Communauté GNU/Linux 7.2 Communauté Slashdot 7.3 Système de gestion de contenu Mambo 8 Autorégulation et droit de l'Internet 8.1 En français 8.2 En anglais 9 Processus émergents d'autorégulation 10 Autorégulation des populations 10.1 Modèles proies-prédateurs de Bernoulli 10.2 Espace des phases et domaine de stabilité 10.3 Raymond Lindeman et l’écologie quantitative 11 Stabilité structurelle, morphogenèse et émergence 11.1 Auto-organisation 11.2 Signature du chaos 11.3 Modèles de Santa-Fe 12 Sujets liés 13 Théoriciens ayant travaillé sur l’autorégulation 14 Mathématiques de l’autorégulation 14.1 Systèmes dynamiques, suites mathématiques 14.2 Équilibre stable 14.3 Valeurs propres 14.4 Cercles de Gerschgorin 14.5 Équations de Volterra-Lotka 14.6 Espace des phases 14.7 Diagramme de Nyquist 15 Notes et références 16 Voir aussi

Trois exemples typiques

La neige

L’exemple le plus simple est celui de la neige : il est commun d’en observer parce qu’elle se trouve être blanche, c’est-à-dire réfléchit la plupart des longueurs d’onde qui l’atteignent, et fond donc d’autant moins vite. Si la neige se trouvait être noire, elle n’en existerait pas moins, mais nous aurions moins le temps de l’observer. Cet exemple montre aussi que l’autorégulation :

• ne nécessite pas la vie ;
• ne nécessite pas de processus intentionnel pour se mettre en place.

Cette considération simple marque la frontière entre l’hypothèse Gaïa de James Lovelock, hypothèse scientifique comme une autre, et la Théorie Gaïa d’aspect plus mystique qui en a été induite par quelques-uns de ses lecteurs, et qui est plus contestée - y compris par Lovelock lui-même.

Les solutions tamponnées en chimie

Les réactions chimiques répondent à une loi d’équilibre nommée loi d'action de masse qui peut être utilisée pour réaliser des solutions-tampon : de telles solutions montrent un pH beaucoup plus stable en présence d’un acide ou d’une base que ne le ferait de l’eau pure : une autorégulation se produit donc.

De tels effets tampon s’observent en biologie, et fournissent une stabilité propice au bon déroulement des processus vitaux.

Autorégulation dans le monde vivant

Dans le cas des êtres vivants, le processus darwinien de sélection naturelle constitue une forme complexe d’autorégulation : en effet, une espèce elle-même ne s’autorégule pas (excepté par l’épuisement de ses ressources), mais un système composé par des proies et des prédateurs s’autorégule selon un mécanisme décrit par l’équation de Bernoulli - faute de quoi proies comme prédateurs disparaissent.

Les autorégulations de la cellule sont étudiées sous le nom d’homéostasie.

Pour la petite histoire, les animaux à sang chaud ont une température autorégulée, ce qui rend bien plus simple le développement de l'embryon. Richard Dawkins signale que le code génétique des batraciens est plus complexe que celui de l'homme, et attribue la différence à la complexité accrue de développement des embryons à température incontrôlée (pour information, la vitesse d'une réaction chimique, y compris biochimique, double à peu près quand la température augmente de 10°C).

Autorégulation physique

Thermostat

Régulateur à boules de James Watt

Le problème de faire conserver à une machine à vapeur une vitesse constante sous la charge sans agir constamment sur ses manettes a été posé et résolu par James Watt.

Autorégulation du Soleil

Le fonctionnement du Soleil est à la base une transformation continue d'hydrogène en hélium par fusion, avec perte continue de masse (4×106 tonnes par seconde).

• Si pour des raisons d'agitation thermique (chaleur de la réaction thermonucléaire) le Soleil augmente de taille, le résultat est un plus grand écartement moyen des atomes d'hydrogène, donc un ralentissement de la réaction.
• Réciproquement, une diminution de taille se traduit par une plus grande densité de l'hydrogène et une plus grande fréquence des réactions de fusion.

Autorégulation en chimie

Principe de Le Châtelier

Le chimiste Henry Le Chatelier remarqua plusieurs phénomène de stabilité dans le monde chimique : une réaction favorisée par la chaleur, par exemple, en absorbait. Une réaction favorisée par la pression se traduisait par une plus grande absorption de gaz, etc. De façon plus générale :

« Toute action suscitait une réaction qui aurait eu l’effet inverse si elle s’était produite seule. »

Il en tira la loi de stabilité de l’équilibre chimique qui porte aujourd’hui son nom^[1].

Loi d’action de masse et effet tampon

La loi de Le Châtelier, qui n’était que qualitative, avait donné naissance à d’autres lois du même ordre comme celle de Van’t Hoff. Les travaux de Guldberg et Waage donnèrent naissance en 1864 à la loi d'action de masse, quantitative, qui fut très étudiée par Marcellin Berthelot et Svante Arrhénius (Berthelot était si admiratif de cette loi qu’il en vint à supposer que la chimie serait bientôt une science achevée). Le comportement bizarre de ces solutions chimiques qui semblaient s’adapter comme rentrent les cornes comme un escargot quand elles touchent un obstacle se révélait n’être en fin de compte qu’une affaire de concentration d’ions conduite spontanément à minimiser un potentiel chimique.

Autorégulation en biologie (cas d’un seul organisme, par opposition aux populations)

Glycémie

Système hormonal

Les hormones jouent un rôle de régulation dans l’organisme, traité dans les articles hormone et homéostasie.

Neurotransmetteurs

Système immunitaire

Expression / promotion / inhibition et autres régulations des gènes

Autorégulation et économie

Il existe au sein d’une société ou d’un groupe d’agents économiques des phénomènes économiques d’autorégulation : il découlent des comportent de rationnalité des agents, et ont été décrit par les sciences économiques.

Ces mécanismes se sont en général mis en place à l’insu des hommes eux-mêmes (du moins en tant que mécanisme de régulation) et que la science économique - qui n’a commencé à vraiment émerger que vers les XVIII^e et XIX^e siècle - a étudié rétrospectivement.

La monnaie

La monnaie constitue un outil de régulation efficace des biens matériels dans une société artisanale, rurale ou nomade, et cela pour une raison stucturelle :

• Les conditions de production les plus favorables (bonne forme physique en début de journée, meilleure terre, meilleures bêtes) étant exploitées en premier (voir : loi des rendements décroissants), le coût de production unitaire augmente dans un tel type de société avec les quantités produites.

• En revanche, ces productions ont elles-mêmes, en raison de la même loi des rendements décroissants appliquée par le consommateur, une utilité de plus en plus faible. L’économiste Charles Gide donne comme exemple^[2] le seau d’eau que l’on extrait du puits :
  • Le premier sert par priorité à assurer la ration d’eau de la famille
  • Le second à donner à boire au bétail
  • Le troisième à arroser le potager
  • Le quatrième à faire un brin de toilette
  • Le cinquième à laver le sol
  • Le sixième peut-être à arroser quelques fleurs d’agrément

La conjonction des coûts unitaires croissants et de la valeur unitaire décroissante garantit que l’on arrivera à un équilibre. Il existera un moment où on ne jugera plus intéressant de tirer du puits, pour ce jour-là, un seul seau d’eau de plus. Le point d’équilibre s’atteint structurellement, et obligatoirement, dans ce cas précis. L’existence de cet équilibre et les forces de retour vers cet équilibre consituent un mécanimse d'autorégulation

Dans le monde réel, toutefois :

• les utilités peuvent ne pas être décroissantes, mais au contraire croissantes (s’il n’existe qu’un téléphone dans le monde, son utilité pour le monde est nulle; plus il en existe, plus l’utilité possible de chacun augmente ou, du moins, il est facile de démontrer qu’elle ne saurait diminuer.

• les coûts unitaires peuvent ne pas être croissants : si mille lecteurs ont besoin d’un journal, celui-ci reviendra relativement cher. Si c’est un million de lecteurs, il sera possible de répartir les coûts sur une plus large base.

L’existence d’un point d’équilibre unique peut alors ne pas être garantie. Il peut par exemple en exister plusieurs distincts qui seront comme autant d’optimums locaux.

Autorégulation du niveau de concurrence

Dans le cas du monopole (concurrence des divers emplois de la monnaie pour le consommateur)

Sauf cas très particuliers (eau, médecine...), le producteur ne peut augmenter indéfiniment son prix, sans quoi le consommateur pourrait à son tour réorienter sa consommation. Ainsi, s’il estime les voyages trop chers, il peut décider d’occuper ses loisirs à autre chose comme le cinéma, le jardinage ou le bricolage.

Dans le cas de l’oligopole (pression bien plus forte à la baisse des coûts)

La « main invisible » d’Adam Smith

Métaphore de la main invisible d’Adam Smith (« l’homme est conduit par une main invisible à remplir une fin qui n’entre nullement dans ses intentions ; tout en ne cherchant que son intérêt personnel »). Ainsi le marché s’autorégule et maximise la seule production; Le consommateur et le producteur, cherchant leur intérêt individuel, participerait à l'amélioration de la société toutefois. Ce modèle ne règle pas le problème de la répartition. (Il faut considérer ce concept sous son seul aspect technique et non sous d’éventuels aspects de propagande ou de dénigrement de la théorie libérale.) En réalité, l'expression de Smith n'apparaît qu'une fois dans La Richesse des nations et dans le contexte d'un raisonnement contre ce que nous appelons aujourd'hui le néolibéralisme. Il avait compris que sa théorie ne fonctionnerait pas s'il y avait libre circulation et libre investissement des capitaux (voir l'article détaillé).

Autres aspects de l’autorégulation en économie

Étudiés par David Ricardo et Vilfredo Pareto qui produisit les lois scalantes : Loi de Pareto dite des 80/20.

Limitations structurelles de l’autorégulation

• Perte d’efficacité de la monnaie comme régulateur avec la révolution industrielle.
  • Importance croissante des frais fixes : la loi des rendements décroissants, même globalement vraie, devient parfois localement fausse.
  • Instabilité associée

Ce phénomène technique peut engendrer des crises économiques.

• Analyse de Karl Marx (se limiter aussi à l’aspect technique; bien que indissociable de l'aspect politique)
• Effets pervers de la non-concavité.
• Problème de la régulation de l’immatériel. Conséquences de quelques dérégulations (le désert des Mojaves).

Autorégulation et politique

• Exemple extrême : « la monarchie absolue tempérée par le régicide ».
• Féodalité
• Monarchie
• Système démocratique bicaméral. Séparation des pouvoirs
  • États-Unis
  • Europe
• Comparaison du scrutin d'arrondissement et de la proportionnelle en matière d’autorégulation.
• Le système de Hare
• Paradoxe de Condorcet
• Théorème d'Arrow
• Au-delà de Condorcet : Modèle de Marcotorchino et Michaud. Data mining.

« En 1794, Le marquis de Condorcet eut à écrire un texte « littéraire » d’un contenu mathématique puissant. Il s’agissait de déterminer l’homme « moyen », le triangle équilatéral moyen en partant de plusieurs triangles équilatéraux. Plus généralement, cela peut se voir en termes de vote à la majorité relative. N votants classent M candidats selon leurs préférences dans l’ordre. Si on l’applique à M produits, c’est le tableau des préférences des consommateurs.

Vu l’état des mathématiques d’alors, il était difficile de trouver une solution satisfaisante à la règle de Condorcet. Même dans les années 60, un « expert » américain Weles a obtenu le « Prix Nobel » d'économie en décrétant un « théorème » de l’impossibilité de l’agrégation des préférences individuelles et du coup la seconde mort de Condorcet. Or dans les années 1980, Michaud et Marcotorchino ont levé le voile sur le paradoxe. Le paradoxe de Condorcet n’en est plus un. Il suffit de d’abord coder la réponse des individus par 1 ou 0, ensuite par un algorithme du simplexe ou une programmation linéaire maximiser la dispersion ou autrement dit augmenter la variance interclasses (il faudra utiliser un lagrangien) pour trouver la solution à la règle du vote à la majorité relative ».^[3].

• Cas particuliers
  • Clientélisme
  • Corporatisme
  • Système africain

Autorégulation des microsociétés

Communauté GNU/Linux

Communauté Slashdot

Les pages 157 à 162 de l'ouvrage de Steven Johnson Emergence (ISBN 0-140-287-752) détaillent également ce phénomène d'autorégulation.

Système de gestion de contenu Mambo

^[4]

Autorégulation et droit de l'Internet

En français

^[5]

En anglais

Processus émergents d'autorégulation

• Autorégulation dans le domaine du logiciel libre

Autorégulation des populations

Modèles proies-prédateurs de Bernoulli

Le modèle linéaire propose l'étude de l'évolution d'une colonie de proies en croissance permanente ; son nom vient de Nicolas Bernoulli.

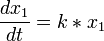
Avec la décroissance de la colonie des prédateurs :

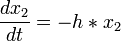
Mais les prédateurs peuvent survivre grâce aux proies :

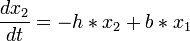
De même la colonie des proies va-t-elle diminuer :

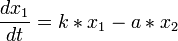
On verra dans une approche avancée le modèle de Volterra-Lotka.

Espace des phases et domaine de stabilité

Raymond Lindeman et l’écologie quantitative

Stabilité structurelle, morphogenèse et émergence

Auto-organisation

Signature du chaos

Modèles de Santa-Fe

Sujets liés

• cybernétique
• automatique
• rétroaction
• homéostasie
• régulateur à boules
• Analyse systémique
• Auto-organisation

Théoriciens ayant travaillé sur l’autorégulation

• Thomas Malthus
• Adam Smith
• Charles Darwin
• Nikolai Kondratiev
• Ross Ashby
• Benoit Mandelbrot

Mathématiques de l’autorégulation

Systèmes dynamiques, suites mathématiques

Une expression simple de l'autorégulation est celle des suites arithmético-géométriques, très liée à la rétroaction :

x(t) = a.x(t − 1) + b

Le système est en équilibre lorsque :

x(t) = x(t − 1)

soit :

x = a.x + b

le point d'équilibre est donc :

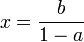
Lorsque | a | < 1, la suite converge toujours vers le point d'équilibre, quelle que soit la valeur initiale, et donc quelle que soit la perturbation ponctuelle appliquée au système.

Lorsque | a | > 1 ou si a = 1, le système diverge et tend vers l'infini : c'est une auto-amplification.

Dans le cas où a = − 1, on a un système oscillant autour de x₀ et − x₀ + b :

x₁ = − x₀ + b

x₂ = − x₁ + b = − ( − x₀ + b) + b = x₀

et donc très sujet à une perturbation ponctuelle, qui modifie le point d'oscillation.

Équilibre stable

Par exemple, en météorologie, des équilibres stables peuvent exister^[6].

Valeurs propres

Lorsqu’au voisinage d’un de ses points d’équilibres un système peut être approximé par un modèle linéaire de rétroaction, alors ses valeurs propres sont nécessairement négatives (ce qui constitue une expression de cette stabilité)^[7].

Cercles de Gerschgorin

Le calcul exact des valeurs propres, incommode pour les matrices de très grande dimension, n’est pas toujours indispensable. Le théorème de Gerschgorin démontre en effet que toutes ces valeurs propres sont situées, dans le plan complexe, à l’intérieur de cercles nommes cercles de Gerschgorin. Indépendamment de l’autorégulation, ces cercles possèdent une caractéristique intéressantes : s’ils sont disjoints, la matrice est inversible (ce qui signifie qu’on peut sans difficulté particulière « remonter le temps » en ce qui concerne l’évolution du système, d’autant plus loin que la précision de l’approximation linéaire du comportement du système autour de ce point de stabilité local est bonne^[7]).

Équations de Volterra-Lotka

L'équation de Volterra-Lotka régit au départ des modèles composés de proies de de prédateurs; qualitativement :

• plus les proies sont nombreuses et plus les prédateurs vont survivre et se reproduire,
• plus les prédateurs sont nombreux à la génération suivante, plus nombreuses sont les proies qui seront alors consommées.
• cela aboutira à au bout de quelque temps à une diminution des proies, donc à une famine des prédateurs et à une réduction de leur nombre

Le résultat peut être un cycle amorti, un cycle non-amorti, ou une excursion qui peut se traduire par la disparition des deux espèces^[8],[9].

Espace des phases

^[10]

Diagramme de Nyquist

^[11]

Notes et références

Voir aussi

• Portail sur les sciences