- Srinivasa Aaiyangar Ramanujan
-
Srinivasa Ramanujan
Srinivâsa Aiyangâr Râmânujan, en tamoul : ஸ்ரீனிவாஸ ஐயங்கார் ராமானுஜன், (22 décembre 1887 – 26 avril 1920) est un mathématicien indien.
Ramanujan travailla principalement en théorie analytique des nombres et devint célèbre pour ses formules sommatoires impliquant des constantes telles que π et e, des nombres premiers et la fonction partage d'un entier obtenue avec Godfrey Harold Hardy.
Ramanujan avait un raisonnement très rapide, ce qui faisait dire à certains de ses contemporains qu'il était un mathématicien « naturel », voire un génie[1].
Sommaire
Biographie
Ramanujan est né à Erode, dans l'actuel État de Tamil Nadu en Inde, dans une famille de brâhmanes pauvre et orthodoxe.
Il était un autodidacte et resta toujours très autonome. Il apprit les mathématiques à partir de deux uniques livres qu'il s'était procurés avant ses 15 ans : La Trigonométrie plane de S. Looney, et Synopsis of Elementary Results in Pure Mathematics de S. Carr qui contenait une liste de quelques 6 000 théorèmes sans démonstration. Ces deux ouvrages lui permirent d'établir une grande quantité de résultats sur la théorie des nombres, les fonctions elliptiques, les fractions continues et les séries infinies, tout en créant son propre système de représentation symbolique pour arriver à ces résultats. Jugeant son entourage académique dépassé, il publia plusieurs articles dans les journaux mathématiques indiens et tenta alors d'intéresser les mathématiciens européens à son travail par des lettres qu'il leur envoyait.
Une lettre de 1913 à Hardy contenait une longue liste de théorèmes sans démonstration. Hardy considéra tout d'abord cet envoi inhabituel comme une supercherie, puis - interpelé par l'étrangeté de certains théorèmes - en discuta longuement avec John Littlewood pour aboutir à la conviction que son auteur était certainement un « homme de génie »[2]. Hardy lui répondit et invita Ramanujan à venir en Angleterre ; une collaboration fructueuse en résulta, en compagnie de Littlewood.
Hardy déclara, à propos de certaines formules qu'il ne pouvait comprendre, qu'« un seul coup d'œil sur ces formules était suffisant pour se rendre compte qu'elles ne pouvaient être pensées que par un mathématicien de tout premier rang. Elles devaient être vraies, parce que personne n'eût pu avoir l'idée de les concevoir fausses »[3]. Hardy aimait classer les mathématiciens sur une échelle de 1 à 100. Il s'attribuait 25, donnait 30 à Littlewood, 80 à David Hilbert et 100 à Ramanujan.
Tourmenté toute sa vie par des problèmes de santé, Ramanujan vit son état empirer en Angleterre ; il retourna en Inde en 1919 et mourut peu de temps après à Kumbakonam (à 260 km de Madras) à l'âge de 32 ans. Il laissa derrière lui des livres entiers de résultats non démontrés (appelés Cahiers de Ramanujan) qui continuent d'être étudiés au début du XXIe siècle.
Formules
Ramanujan a donné la formule suivante :
Cette formule relie parfaitement une série infinie et une fraction continue pour donner une relation entre les deux plus célèbres constantes des mathématiques.
Jonathan et Peter Borwein ont démontré une deuxième formule qu'il avait découverte en 1910 :
Elle est très efficace puisqu'elle fournit 8 décimales à chaque itération.
Nombres de Ramanujan
- Un « nombre de Ramanujan » est un entier naturel qui peut s'exprimer comme la somme de deux cubes de deux façons différentes.
Hardy rapporte l'anecdote suivante : « Je me souviens que j'allais le voir une fois, alors qu'il était malade, à Putney. J'avais pris un taxi portant le numéro 1729 et je remarquai que ce nombre me semblait peu intéressant, ajoutant que j'espérais que ce ne fût pas mauvais signe.
- Non, me répondit-il, c'est un nombre très intéressant : c'est le plus petit nombre décomposable de deux manières différentes en somme de deux cubes. » En effet, 93 + 103 = 13 + 123 = 1729.
- D'autres nombres ayant cette propriété avaient été trouvés par le mathématicien français Bernard Frénicle de Bessy (1602-1675) :
- 23 + 163 = 93 + 153 = 4104
- 103 + 273 = 193 + 243 = 20683
- 23 + 343 = 153 + 333 = 39312
- 93 + 343 = 163 + 333 = 40033
- Le plus petit nombre décomposable de deux manières différentes en somme de deux puissances quatrièmes est 635 318 657, et c'est Euler (1707-1783) qui l'a trouvé : 1584 + 594 = 1334 + 1344 = 635318657.
- Un nième nombre taxicab, noté Ta(n) ou Taxicab(n), est le plus petit nombre qui peut être exprimé comme une somme de deux cubes positifs non nuls de n façons distinctes à l'ordre des opérandes près. Ainsi, Ta(1) = 2 = 13 + 13, Ta(2) = 1729 et Ta(3) = 87539319. Il existe une variante du nombre taxicab : un nombre cabtaxi est défini comme le plus petit nombre entier pouvant s'écrire de n façons différentes (à l'ordre des termes près) comme somme de deux cubes positifs, nuls ou négatifs.
- La preuve, de l'Américain David Auburn, est une pièce de théâtre évoquant ce concept. Elle a reçu un prix Pulitzer (2001). Les deux personnages principaux sont un mathématicien de génie qui a sombré dans la folie et sa fille qui doit prendre la relève. Une version française, en 2002, réunissait Rufus dans le rôle du mathématicien et Anouk Grinberg (puis Elsa Zylberstein) dans celui de la fille.
Annexes
Bibliographie
- Godfrey Harold Hardy, L'Apologie d'un mathématicien, Éditions Belin, 1985. ISBN 2-7011-0530-7
- Bernard Randé, Les carnets indiens de Srivanasa Ramanujan, Éditions Cassini, 2002. ISBN 2-84225-065-6
- G.H. Hardy, The Indian Mathematician Ramanujan, American Mathematical Monthly, Vol.44, n°3, mars 1937, pp 137-155.
Notes et références
- ↑ « Hardy décida que Ramanujan avait autant de génie naturel que Gauss ou Euler » C.P. Snow, postface de Hardy, l'apologie d'un mathématicien, Belin, 1985.
- ↑ C. P. Snow, postface de Hardy, l'apologie d'un mathématicien, Belin, 1985.
- ↑ G. H. Hardy, « Ramanujan, un mathématicien indien » dans Hardy, l'apologie d'un mathématicien, Belin, 1985
Voir aussi
Articles connexes
Liens externes
- (fr) Panorama sur différents aspects de sa personne
- (en) Quelques notes sur sa vie et ses publications (format PostScript)
- (en) Sa vie et son travail sur McTutor
- (en) Journal dédié à sa vie, son travail et les domaines des mathématiques qu'il a influencés
- Portail du monde indien
- Portail des mathématiques
Catégories : Mathématicien indien | Membre de la Royal Society | Tamil Nadu | Naissance en 1887 | Décès en 1920
Wikimedia Foundation. 2010.


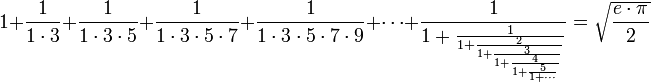
![\pi = \frac{9801}{2\sqrt{2} \displaystyle\sum^\infty_{n=0} \frac{(4n)!}{(n!)^4} \times \frac{[1103 + 26390n]}{(4 \times 99)^{4n}}}](/pictures/frwiki/102/f47c56ad9410cd56d2004aa1557f9d7f.png)
