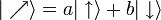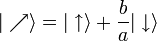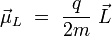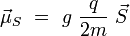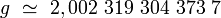- Spin (physique)
-
Spin
 Pour les articles homonymes, voir Spin (homonymie).
Pour les articles homonymes, voir Spin (homonymie).Le spin est une propriété quantique intrinsèque associée à chaque particule, qui est caractéristique de la nature de la particule, au même titre que sa masse et sa charge électrique. Comme la majorité des observables quantiques, sa mesure donne des valeurs discontinues et est soumise au principe d'incertitude.
Le spin a été expérimentalement mis en évidence en 1922 dans l'expérience de Stern et Gerlach et a été d'abord interprété comme le moment angulaire d'une rotation de la particule sur elle-même, autour d'un axe. Cette image est correcte dans la mesure où le spin peut être modélisé par les mêmes lois mathématiques qu'un moment angulaire (quantique), mais comme cette interprétation implique une propriété géométrique qui est en contradiction avec la relativité, elle a été abandonnée. On désigne parfois le spin comme un moment angulaire (ou cinétique) intrinsèque[1], c'est à dire répondant aux mêmes lois algébriques, sans correspondre à la représentation géométrique que l'on s'en fait.
En 1927, Wolfgang Pauli a proposé la modélisation du spin en termes de matrices, ce qui correspond à une écriture en termes d'opérateurs sur la fonction d'onde intervenants dans l'équation de Schrödinger : l'équation de Pauli. En 1928, Paul Dirac en a démontré la version relativiste : l'équation de Dirac. En 1940, Eugène Wigner a démontré que le spin est l'un de deux invariants (avec la masse) quand on fait subir à un vecteur d'un espace de Hilbert, décrivant un système quantique, des transformations correspondant à des translations, des rotations et des symétries dans l'espace-temps à quatre dimensions de la relativité restreinte (ces opérations formant le groupe des isométries de l'espace de Minkowski appelé le groupe de Poincaré)[2].Cela mène à la définition moderne du spin : le spin permet de caractériser le comportement du champ associé à une particule sous l'effet de la symétrie de rotation de l'espace.
Le spin a d'importantes implications théoriques et pratiques. Il est responsable du Moment magnétique de spin et donc de l'effet Zeeman anomal[3] qui en découle. Les particules sont classées selon la valeur de leur spin : les bosons de spin entier et les fermions de spin demi-entier. Fermions et bosons se comportent différemment dans des systèmes comprenant plusieurs particules identiques ; le comportement fermionique de l'électron est ainsi la cause du principe d'exclusion de Pauli, des régularités de la table périodique des éléments, et de la stabilité des liaisons chimiques. L'interaction spin-orbite conduit à la structure fine du spectre atomique. Le spin de l'électron joue un rôle important dans le magnétisme, et la manipulation des courants de spins dans des nano-circuits conduit à un nouveau champ de recherche : la spintronique. La manipulation des spin nucléaires par résonance magnétique nucléaire est importante dans la spectroscopie chimique et l'imagerie médicale (IRM). Le spin du photon – ou plus exactement son hélicité – est associé à la polarisation de la lumière.
Sommaire
Spin des particules usuelles
Comme la plupart des observables, le spin est représentable par un vecteur[1] dont toute mesure est quantifiée (les mesures donnent des valeurs discontinues), et surtout le principe d'incertitude s'applique aux mesures du spin faites dans les différentes directions de l'espace : on peut mesurer précisemment la norme du vecteur et une projection sur un axe de coordonnées, mais les deux autres projections sur les deux autres axes ne sont plus alors mesurables. Mathématiquement, cela est dû au fait que les trois opérateurs de projections du spin
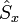 ,
, 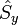 ,
, 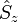 ne commutent pas entre eux, mais tous commutent avec
ne commutent pas entre eux, mais tous commutent avec 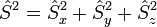 l'opérateur de la norme (au carré).
l'opérateur de la norme (au carré).Les propriétés algébriques des opérateurs du spin impliquent qu'il existe un nombre s dit entier ou « demi-entier », c-est-à-dire pris dans l'ensemble {0, 1/2, 1, 3/2, 2, ...} et nommé spin, tel que la mesure de la norme du vecteur donne
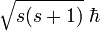 et que la mesure de la projection du vecteur sur un axe quelconque donne un résultat parmi les 2 s + 1 valeurs possibles
et que la mesure de la projection du vecteur sur un axe quelconque donne un résultat parmi les 2 s + 1 valeurs possibles 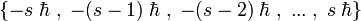 .
.Pour une raison assez complexe démontrée dans le cadre de ce qui est appelé théorème spin-statistique, le valeur entière ou demi-entière du spin détermine une propriété cruciale de la particule : si son spin est entier, c'est un boson, si son spin est demi-entier, c'est un fermion.
La totalité des particules connues ou d'existence fortement suspectée à un spin compris entre 0 et 2. En particulier
- Spin 0 : le boson de Higgs, particule hypothétique, non encore découverte expérimentalement.
- Spin 1/2 : l'électron, le positron, le proton, le neutron, les neutrinos, les quarks, etc.
- Spin 1 : le photon, les bosons W± et Z0, vecteurs de l'interaction faible.
- Spin 2 : le graviton, particule hypothétique vecteur de la gravitation.
Il n'existe pas de particule élémentaire connue de spin 3/2, mais la supersymétrie, si elle existe, en prédit une, le gravitino.
Le spin de particules composées de plusieurs particules élémentaires, comme le proton, le neutron, tout noyau atomique ou atome, est constitué des spins des particules qui les composent auxquels s'ajoute leur éventuel moment angulaire orbital.
Historique
Le spin de l'électron a été expérimentalement mis en évidence en 1922 dans l'expérience de Stern et Gerlach et a d'abord été interprété comme une rotation de la particule autour d'un axe (comme son nom l'indique en anglais) en 1923[4] par George Uhlenbeck et Samuel Goudsmit, mais Wolfgang Pauli a montré en 1924 que, compte tenu des dimensions connues de l'électron, cela nécessitait une vitesse de rotation à son équateur qui serait supérieure à la vitesse de la lumière. Dès lors la représentation du spin en termes de rotation n'a plus été utilisée en dehors d'un cadre de vulgarisation.
La notion théorique de spin a été introduite par Pauli en décembre 1924[5] pour l'électron, afin d'expliquer un résultat expérimental qui restait incompréhensible dans le cadre naissant de la mécanique quantique non relativiste : l'effet Zeeman anomal. L'approche développée par Pauli consistait à introduire de façon ad-hoc le spin en ajoutant un postulat supplémentaire aux autres postulats de la mécanique quantique non relativiste (équation de Schrödinger, etc.).
En 1927, Wolfgang Pauli a proposé la modélisation du spin en termes de matrices, ce qui correspond à une écriture en termes d'opérateurs sur la fonction d'onde intervenants dans l'équation de Schrödinger : l'équation de Pauli. En 1928, à partir de l'équation de Klein-Gordon, Paul Dirac démontra qu'une particule ayant un spin non-nul vérifie une équation relativiste, appelée aujourd'hui équation de Dirac.
Enfin, c'est en théorie quantique des champs que le spin montre son caractère le plus fondamental. L'analyse du groupe de Poincaré effectuée par Wigner en 1939 montra en effet qu'une particule est associée à un champ quantique, opérateur qui se transforme comme une représentation irréductible du groupe de Poincaré. Ces représentations irréductibles se classent par deux nombres réels positifs : la masse et le spin.
Le spin du photon a été découvert expérimentalement par Raman et Bhagavantam en 1931[6].
« Rotation propre »
Historiquement, le spin a d'abord été interprété par Samuel Goudsmit et George Uhlenbeck en septembre 1925[7],[8] comme étant un moment cinétique intrinsèque, c'est-à-dire dû à une rotation de la particule sur elle-même. Cette vision classique d'une rotation propre de la particule est en fait trop naïve. En effet, si la particule est ponctuelle, la notion de rotation propre autour de son axe est tout simplement dénuée de sens physique[9]. Si à l'inverse la particule n'est pas ponctuelle, alors la notion possède un sens, mais on se heurte dans ce cas à une autre difficulté[10]. Supposons par exemple que la particule soit un électron, modélisé comme étant un corps sphérique de rayon a. On obtient une estimation de ce rayon en écrivant que l'énergie de masse de l'électron est de l'ordre de grandeur de son énergie potentielle électrostatique, soit :
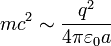 ,
,
où q est la charge électrique de l'électron, m sa masse, c la vitesse de la lumière et ε0 la permittivité du vide. La valeur numérique de ce rayon classique de l'électron est de l'ordre de 10-15 mètre. Si l'on attribue alors à cet électron un moment cinétique égal à ℏ / 2, on obtient pour un point de l'équateur une vitesse v vérifiant :
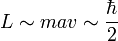 ,
,
ce qui, en combinant avec l'équation précédente donne
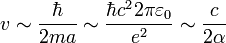 ,
,
où l'on a introduit la constante de structure fine α. α étant bien plus petite que 1, la valeur obtenue de la vitesse est très supérieure à celle de la lumière, en contradiction avec la relativité restreinte.
De fait, aucune description purement mécanique de la nature du spin n'est en mesure de rendre compte des propriétés observées. En particulier il est difficile de conceptualiser à quoi un spin demi-entier peut correspondre pour une particule élémentaire.
Formalisme de Pauli
Opérateur spin
En mécanique quantique, le spin est un opérateur vectoriel hermitien comportant trois composantes, notées usuellement
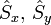 et
et 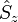 par référence aux trois axes de coordonnées cartésiennes de l'espace physique. Ces composantes sont des observables vérifiant les relations de commutations caractéristiques d'un moment cinétique :
par référence aux trois axes de coordonnées cartésiennes de l'espace physique. Ces composantes sont des observables vérifiant les relations de commutations caractéristiques d'un moment cinétique :où εijk est le symbole de Levi-Civita. Ces relations de commutations sont analogues à celles découvertes en novembre 1925 par Born, Heisenberg et Jordan pour les composantes du moment cinétique orbital :
![\left[ \, \hat{L}_i \, , \ \hat{L}_j \, \right] \ = \ i \ \hbar \ \epsilon_{ijk} \ \hat{L}_k](/pictures/frwiki/53/50b2055de1bf66ce973994caf003e045.png)
Par analogie avec les résultats obtenus pour le moment cinétique orbital (ou plus généralement pour un moment cinétique quantique), il existe pour l'opérateur spin une base de vecteurs propres notés | s,ms > , où s est entier ou demi-entier, et ms est un entier ou demi-entier prenant l'une des 2s + 1 valeurs
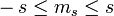 , tels que :
, tels que :Spin 1/2 - matrices de Pauli
Article détaillé : Matrices de Pauli.Pour une particule de spin 1/2 comme l'électron, on a s = 1 / 2, donc 2s + 1 = 2 : il existe seulement deux états de spin distincts, caractérisés par
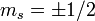 .
.On note souvent les deux états propres correspondant :
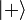 et
et 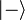 , ou encore symboliquement :
, ou encore symboliquement : 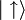 et
et 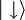 .
.Pauli a introduit trois matrices 2 x 2, notées
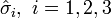 telles que l'opérateur de spin s'écrive :
telles que l'opérateur de spin s'écrive :Ces trois matrices de Pauli s'écrivent explicitement :
Elles satisfont les relations de commutation :
Représentation géométrique du spin par une sphère de Riemann
Un état quantique quelconque d'une particule de spin 1/2 peut s'exprimer sous la forme générale :
(a et b étant deux nombres complexes). Cette formule exprime une superposition des deux états propres.
Selon les règles de la mécanique quantique, l'état quantique représenté par
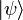 et
et 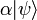 sont physiquement rigoureusement les mêmes. Par conséquent, on peut également exprimer l'état général d'une particule de spin 1/2 par:
sont physiquement rigoureusement les mêmes. Par conséquent, on peut également exprimer l'état général d'une particule de spin 1/2 par:L'état de spin 1/2 est donc entièrement caractérisé par un nombre complexe
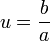 . Ce rapport pouvant être infini quand a = 0 (état pur de spin "down"), il est nécessaire d'utiliser une sphère de Riemann pour représenter ce rapport, la sphère de Riemann étant une extension du corps des complexes avec l'infini. Dans ce contexte, la sphère de Riemann est également appelée la sphère de Bloch dans le cas de l'électron, ou la sphère de Poincaré dans le cas du photon.
. Ce rapport pouvant être infini quand a = 0 (état pur de spin "down"), il est nécessaire d'utiliser une sphère de Riemann pour représenter ce rapport, la sphère de Riemann étant une extension du corps des complexes avec l'infini. Dans ce contexte, la sphère de Riemann est également appelée la sphère de Bloch dans le cas de l'électron, ou la sphère de Poincaré dans le cas du photon.Selon cette représentation, tout état de spin 1/2 trouve une représentation géométrique (voir figure ci-contre). Le vecteur passant par l'origine et pointant sur la projection du complexe u sur la sphère de Riemann donne une visualisation géométrique de l'état de spin 1/2 comme étant une direction dans l'espace.
Bien que semblant a priori purement mathématique, cette représentation de l'état de spin comme étant une direction dans l'espace possède une certaine pertinence. Notamment, on peut retrouver simplement à l'aide de cette représentation géométrique la probabilité d'obtenir l'état
 et
et  lors d'une mesure de l'état
lors d'une mesure de l'état 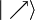 (il ne faut pas perdre de vue que l'état mesuré d'un état de spin 1/2 sera toujours soit
(il ne faut pas perdre de vue que l'état mesuré d'un état de spin 1/2 sera toujours soit 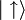 soit
soit 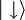 ).
).Moment magnétique de spin
Article détaillé : Moment magnétique de spin.Définition. Facteur de Landé
Au moment cinétique orbital d'une particule de charge q et de masse m est associé un moment magnétique orbital :
Le facteur q / 2m est appelé rapport gyromagnétique. De même, on associe à une particule de charge q, de masse m, et de spin donné un moment magnétique de spin :
où g est un nombre sans dimension, appelé facteur de Landé (1921). Ce nombre varie selon la nature de la particule : on a approximativement g = 2 pour l'électron, g = 5,586 pour le proton, et
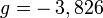 pour le neutron[11]. On trouve aussi des valeurs moitié pour le proton et le neutron qui correspondraient à un moment magnétique anomal.
pour le neutron[11]. On trouve aussi des valeurs moitié pour le proton et le neutron qui correspondraient à un moment magnétique anomal.Magnéton de Bohr
Article détaillé : magnéton de Bohr.Pour l'électron, on a les valeurs suivantes :
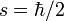 et g = 2,002 ; on introduit alors le « quantum magnétique » suivant, appelé magnéton de Bohr :
et g = 2,002 ; on introduit alors le « quantum magnétique » suivant, appelé magnéton de Bohr :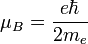
Moment magnétique anomal de l'électron
Article détaillé : Moment magnétique anomal.L'équation de Dirac prédit pour l'électron un facteur de Landé exactement égal à : g = 2. Or, la valeur expérimentale admise en 2005 vaut :
Il existe donc un écart, décelé pour la première fois en 1947 dans la structure hyperfine de l'hydrogène et du deutérium[12] : on parle alors du moment magnétique anomal de l'électron. La théorie quantique des champs du modèle standard permet de rendre compte de cette anomalie avec une très grande précision.
Spin et représentation de groupes
L'analyse du comportement des objets sous l'effet des rotations nécessite de prendre en compte la structure mathématique de groupe formé par celles-ci. À un objet se transformant sous les rotations est alors associée une représentation de groupe. Deux objets ayant des propriétés de symétrie similaires seront donc associés à des représentations équivalentes du groupe des rotations. De ce point de vue, le spin n'est rien d'autre qu'un nombre qui permet de classifier les différentes représentations irréductibles non-équivalentes du groupe des rotations.
Notes et références
- ↑ a et b Toute la physique, article Spin, éditeur Dunod, 1999.
- ↑ voir Steven Weinberg, The Quantum Theory of Fields, Cambridge University Press, Chap. 1 (ISBN 978-0521670531)
- ↑ Le terme anomal était utilisé initialement en français, mais semble aujourd'hui délaissé en faveur de anormal. Voir Gérald Antoine et Robert Martin, Histoire de la langue française, 1914-1945, t. 2, CNRS-Editions, 1049 p. (ISBN 9782271053879), page 375.
- ↑ Initiation à la mécanique quantique, par Élie Belorizki, Dunod éditeur, 2000, ISBN 2100050117.
- ↑ Wolfgang Pauli ; Zeitschrift fur Physik 31 (1925) 373
- ↑ Indian J. Phys. 6 353-366 (1931)
- ↑ Un problème de facteur 2 dans la structure fine du spectre de l'hydrogène, identifié par Heisenberg, fut résolu en décembre 1925 avec l'aide d'Einstein, sous l'impulsion de Bohr. Ce dernier demanda à deux physiciens hollandais de publier le résultat en urgence : S. Goudsmit & G.E. Uhlenbeck, Nature, 117, 264 (1926).
- ↑ George E. Uhlenbeck & Samuel Goudsmit, Naturwissenschaften, 13, 953 (1925).
- ↑ Par définition, l'axe de rotation d'un objet est le lieu de points de cet objet qui restent immobiles. Si la particule est ponctuelle, son axe propre est sur la particule, donc celle-ci est immobile.
- ↑ Il faudrait aussi expliquer quelles sont les forces internes qui assurent la cohésion de cet électron étendu. Ce problème a occupé un grand nombre de théoriciens dans les années 1895 à 1930, avant que l'électrodynamique quantique et son électron ponctuel ne deviennent bien établies.
- ↑ Bien que le neutron ait une charge q = 0, on lui attribue ici un facteur de Landé correspondant au moment magnétique de spin calculé pour la valeur q = e, afin de le comparer à ceux de l'électron et du proton.
- ↑ Marc Knecht ; The anomalous magnetic moments of the electron and the muon, séminaire Poincaré (Paris, 12 octobre 2002) [pdf][lire en ligne], publié dans : Bertrand Duplantier et Vincent Rivasseau (Eds.) ; Poincaré Seminar 2002, Progress in Mathematical Physics 30, Birkhäuser (2003), ISBN 3-7643-0579-7.
Voir aussi
Liens internes
- Principe d'exclusion de Pauli
- Physique des particules
- Mécanique quantique
- Symétrie (physique)
- Principe d'incertitude
- Théorie quantique des champs
- Moment cinétique quantique
- Moment cinétique orbital
- Moment magnétique de spin
- Moment magnétique anomal
Bibliographie
- Wolfgang Pauli ; Zeitschrift fur Physik 31 (1925) 373.
- George E. Uhlenbeck et Samuel Goudsmit ; Naturwissenschaften 13 (1925) 953.
- Samuel Goudsmit et George E. Uhlenbeck ; Nature 117 (1926) 264.
- Sin-Itiro Tomonaga ; The story of spin, The university of Chicago press (1997), ISBN 0-226-80794-0. Traduction anglaise d'un ouvrage paru en japonais en 1974.
- Marc Knecht ; The anomalous magnetic moments of the electron and the muon, séminaire Poincaré (Paris, 12 octobre 2002), publié dans : Bertrand Duplantier et Vincent Rivasseau (Eds.) ; Poincaré Seminar 2002, Progress in Mathematical Physics 30, Birkhäuser (2003), ISBN 3-7643-0579-7.
- Portail de la physique
Catégories : Physique théorique | Physique quantique
Wikimedia Foundation. 2010.

![\left[ \, \hat{S}_i \, , \ \hat{S}_j \, \right] \ = \ i \ \hbar \ \epsilon_{ijk} \ \hat{S}_k](/pictures/frwiki/53/56736a4c37a2470ddb3bc4bf03c15bab.png)
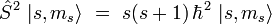
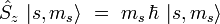
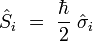
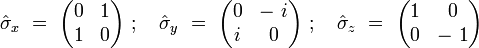
![\left[ \, \hat{\sigma}_i \, , \ \hat{\sigma}_j \, \right] \ = \ 2 \ i \ \epsilon_{ijk} \ \hat{\sigma}_k](/pictures/frwiki/102/f0e84d8251c96b1f008b317be9a55e54.png)