Résistance des matériaux

Pour les articles homonymes, voir Résistance.

Essai de compression sur une éprouvette de béton, une pression croissante est appliquée verticalement sur l'échantillon pendant que deux appareils mesurent les déformations longitudinales et transversales de l'éprouvette

À l'issue du test, l'éprouvette s'est rompue. Notez la cassure longitudinale

La résistance des matériaux, aussi appelée RDM, est une discipline particulière de la mécanique des milieux continus permettant le calcul des contraintes et déformations dans les structures des différents matériaux (machines, génie mécanique, bâtiment et génie civil).

La RDM permet de ramener l'étude du comportement global d'une structure (relation entre sollicitations — forces ou moments — et déplacements) à celle du comportement local des matériaux la composant (relation entre contraintes et déformations). L'objectif est de concevoir la structure suivant des critères de résistance, de déformation admissible et de coût financier acceptable.

Lorsque l'intensité de la contrainte augmente, il y a d'abord déformation élastique (le matériau se déforme proportionnellement à l'effort appliqué et reprend sa forme initiale lorsque la sollicitation disparaît), suivie parfois (en fonction de la ductilité du matériau) d'une déformation plastique (le matériau ne reprend pas sa forme initiale lorsque la sollicitation disparaît, il subsiste une déformation résiduelle), et enfin rupture (la sollicitation dépasse la résistance intrinsèque du matériau).

Histoire

Le premier cours de Résistance des Matériaux est donné par August Wöhler à l'université de Göttingen en 1842.^{[réf. nécessaire]}

Démarche générale

Démarche de calcul manuel avec la théorie des poutres

La résistance des matériaux est utilisé pour concevoir des systèmes (structures, mécanismes) ou pour valider l'utilisation de matériel. On se place dans le cas d'une déformation réversible : une déformation irréversible (déformation plastique ou rupture) rendrait la pièce inopérante. Il faut donc vérifier deux choses :

1. Que l'on reste bien dans le domaine élastique, par l'application d'un critère de ruine : c'est la vérification de l'état limite ultime (ELU).
2. Que la déformation élastique sous charge est compatible avec la fonction de la pièce : c'est la vérification de l'état limite en service (ELS).

Pour effectuer les calculs de validation, il faut passer par une étape de modélisation :

• étude statique : détermination des efforts extérieurs auxquels est soumise la pièce étudiée ;
• modélisation du matériau : cela consiste à déterminer des valeurs caractéristiques du matériau par des essais mécaniques, en particulier l'essai de traction ; on s'intéresse en général à la limite d'élasticité R_e pour l'ELU, et au module de Young E pour l'ELS ;
• modélisation de la pièce : pour des calculs à la main, on utilise des modèles simples (poutre pour des pièces élancées, plaques ou coques pour des pièces minces) ; le calcul par ordinateur (éléments finis) utilise un modèle numérique de la structure (dans un logiciel de CAO).

L'application des lois de l'élasticité permet de déterminer le tenseur des contraintes. On compare ensuite les valeurs des contraintes avec les limites d'élasticité du matériau, en utilisant un « critère de ruine », pour valider ou invalider à l'ELU.

Les lois de l'élasticité permettent également de déterminer le champ de déplacement, ce qui permet de valider ou d'invalider à l'ELS.

Hypothèses de la résistance des matériaux

Dans son utilisation courante, la RDM fait appel aux hypothèses suivantes :

Le matériau est :

• élastique (le matériau reprend sa forme initiale après un cycle chargement déchargement),
• linéaire (les déformations sont proportionnelles aux contraintes),
• homogène (le matériau est de même nature dans toute sa masse),
• isotrope (les propriétés du matériau sont identiques dans toutes les directions).

Le problème est :

• en petits déplacements (les déformations de la structure résultant de son chargement sont négligeables et n'affectent pratiquement pas sa géométrie),
• quasi-statique (pas d'effet dynamique),
• quasi-isotherme (pas de changement de température).

Ces simplifications permettent de faire des calculs simples et rapides, automatisés (par ordinateur) ou à la main. Elles sont toutefois parfois inadaptées, en particulier :

• on utilise fréquemment des matériaux fortement hétérogènes ou anisotropes, comme par exemple les matériaux composites, le bois, le béton armé ;
• certaines applications impliquent des déformations élastiques importantes, notamment avec des matériaux souples (matériaux composites, polymères), on n'est alors plus dans le domaine linéaire ni dans celui des petits déplacements.

Notons enfin que la déformation plastique est un « mécanisme de protection » contre la rupture, en dissipant l'énergie de déformation. Sa prise en compte dans les aciers permet de concevoir des structures métalliques plus légères (par exemple Annexe 80 des Règles de calcul des constructions en acier CM66) ; ceci appartenant encode au cadre non-linéaire et des grands déplacements.

La déformation reste néanmoins toujours limitée ; le domaine des très grandes déformations appartient plutôt au cadre de la rhéologie.

Notion de poutre

L'ingénieur utilise la résistance des matériaux avant tout pour déterminer les dimensions des éléments de construction et vérifier leur résistance et leur déformation. L'un des éléments structurels le plus fréquent est la poutre, c'est-à-dire un objet de grande longueur par rapport à sa section, chargée dans son plan moyen de symétrie.

Sollicitations

Sollicitations élémentaires

Principes fondamentaux de la théorie des poutres

Deux des dimensions de la poutre sont petites par rapport à la troisième. En d'autres termes les dimensions de la section droite sont petites par rapport à la longueur de la poutre. Ce principe permet d'approximer la poutre par une ligne (droite ou courbe) et des sections droites.

En général, une longueur ou une distance de l'ordre de deux à trois fois la plus grande dimension de la section droite est considérée suffisante pour appliquer le modèle RDM.

Le principe de Saint-Venant précise que le comportement en un point quelconque de la poutre, pourvu que ce point soit suffisamment éloigné des zones d'applications des forces et des liaisons, est indépendant de la façon dont sont appliquées les forces et de la façon dont sont physiquement réalisées les liaisons; le comportement dépend alors uniquement du torseur des forces internes en ce point.

La conséquence est que les contraintes produites par un système de forces dans une section éloignée du point d'application de ces forces ne dépendent que de la résultante générale et du moment résultat du système de forces appliquées à gauche de cette section^[1].

Le modèle RDM n'est plus valide lorsque le principe de Saint Venant n'est pas satisfait, c'est-à-dire à proximité des liaisons, des appuis ou des points d'application des forces. Dans ces cas particuliers, il faut appliquer les principes de la mécanique des milieux continus.

Le principe de Navier-Bernoulli précise que les sections droites le long de la fibre moyenne^[2] restent planes après déformation. Les déformations dues à l'effort tranchant montrent que les sections droites ne peuvent pas rester planes mais subissent un gauchissement. Pour tenir de ce fait l'énoncé de ce principe peut prendre la forme suivante: deux sections droites infiniment voisines deviennent après déformation deux sections gauches superposables par déplacement. Comme ce déplacement est petit, on peut considérer que les allongements ou raccourcissements de tout tronçon de fibre sont des fonctions linéaires des coordonnées de la fibre dans le plan de la section^[1].

La loi de Hooke précise que, dans le domaine élastique du matériau, les déformations sont proportionnelles aux contraintes.

Le principe de superposition permet de décomposer toute sollicitation complexe en une somme de sollicitations élémentaires dont les effets sont ensuite additionnés. Ce principe est directement lié à l'hypothèse de linéarité de la loi de Hooke.

L'équilibre statique d'un système exige que :

• La somme des forces extérieures en tout point est égale au vecteur nul : .
• La somme des moments calculés en tout point est égale au vecteur nul : .

Le théorème de Castigliano définit le déplacement du point, lieu d'application d'une force, par la dérivée du potentiel élastique par rapport de cette force.

Quelques notations et définitions

La terminologie employée suivant la grandeur étudiée dépend du point de vue par rapport à la pièce étudiée.

Les efforts (ou chargement) regroupent les forces (en multiples du N) et les moments (en multiples du Nm). Les déplacements sont l'ensemble des translations (en unités de longueur compatibles avec celles utilisées pour les moments) et des rotations (en radians).

Contraintes mécaniques élémentaires

Loi de Hooke simplifiée à une seule dimension

La contrainte normale σ est proportionnelle à l’allongement relatif ε et un facteur constant E désigné sous le nom de module d'élasticité ou encore module d'Young (valable uniquement pour les petits déplacements) :

• σ est une contrainte qui s'exprime le plus souvent en MPa ou N/mm² ;
• E est homogène à une contrainte ;
• ε est sans dimension.

L’allongement relatif est le rapport entre les longueurs initiale et finale  :

Traction / Compression

Cette contrainte est dite contrainte normale due à la force de traction. σ est égale à l'intensité de la force F divisée par l'aire S de la surface normale à cette force :

avec S la section initiale (avant déformation). σ est aussi appelée contrainte PK1.

Le critère de résistance est rempli lorsque la contrainte maximale reste inférieure à la contrainte limite. La première correspond à la contrainte calculée ci-dessus, éventuellement multipliée par divers facteurs tels que :

• un facteur de concentration de contraintes K_t qui dépend de la géométrie de la poutre (ex : pour une vis à filets triangulaires K_t = 2,5) ;
• un facteur d'amplification dynamique ;
• divers autres facteurs de sécurité (sur les sollicitations).

La contrainte limite correspond généralement à la limite élastique R_e, éventuellement divisée par des facteurs de sécurité (sur la résistance) s_i (ex : pour les gaines d'un ascenseur s = 12).

Flexion

Sous l'effet du moment de flexion M₃ (en Nm), la contrainte de flexion à une distance x₂ (en m) de la fibre neutre s'exprime en fonction du moment quadratique I₃ (en m⁴) de la section étudiée par la relation :

avec

,

le moment quadratique, qui est habituellement désigné par inertie de la section par rapport à l'axe du moment de flexion.

• Pour une section rectangulaire de base b et de hauteur h : .
• Pour une section circulaire de rayon r : .

Le théorème de Huygens permet de calculer le moment quadratique d'une section coupée en plusieurs morceaux. Pour chaque morceau, son moment par rapport à un axe arbitraire A dépend de son moment par rapport à l'axe de gravité G parallèle à A, à sa section S et la distance entre les axes A et G selon l'expression :

.

Cisaillement

avec le module de cisaillement (homogène à une contrainte)

.

Pour avoir la contrainte tangentielle maximale :

• pour une section rectangulaire :
• pour une section circulaire :

Torsion

Ce qui suit concerne uniquement les poutres à sections circulaires.

où θ est l'angle unitaire de torsion (en rad/m). La rotation de la barre en un point d’abscisse L est donc θL.

Le moment quadripolaire I₀ de la section est donné par :

.

La contrainte de cisaillement maximale τ est

.

Étude de la déformation d'une poutre fléchie

On peut obtenir l'allure de la déformée de la poutre en flexion à partir de l'équation différentielle

En intégrant 2 fois, et en déterminant les constantes selon les conditions aux limites, il est possible de trouver la forme de la déformée de la poutre en flexion.

Références théoriques

• La contrainte normale σ : contrainte
• L’allongement relatif  : tenseur des déformations
• Le module d’élasticité longitudinal E ou module de Young : module de Young
• Le module de cisaillement G ou le module d’élasticité tangentiel ou encore module de glissement : module de cisaillement
• Le coefficient de Poisson ν : coefficient de Poisson
• L'inertie I : moment d'inertie

Contraintes mécaniques composées

Cas simple d'une poutre uniformément chargée : réactions aux appuis, efforts tranchants (V(x)) et moments fléchissants (M(x))

La poutre est généralement composée d'un matériau isotrope homogène et chargée dans son plan moyen, vertical le plus souvent. Dans ces conditions, l'ensemble des efforts extérieurs appliqué d'un côté d'une section droite quelconque se ramène à :

• un effort longitudinal de compression ou traction : l'effort normal ;
• un effort normal de cisaillement : l'effort tranchant ;
• un moment fléchissant.

Ce sont les éléments de réduction des charges extérieures au droit de la section considérée.

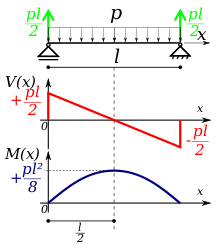
Un cas simple est constitué par une poutre droite, horizontale, de section constante, chargée uniformément et reposant sur deux appuis simples. Si on désigne par p la charge constante et linéaire, et par la longueur de la poutre, la détermination des éléments de réduction des efforts tient en quelques formules simples :

• la réaction à chaque appui est une force verticale, égale à la moitié de la charge totale soit ,
• l'effort tranchant varie linéairement de à avec une valeur nulle en milieu de travée. On doit vérifier que la contrainte de cisaillement au voisinage de l'appui reste inférieure à la résistance au cisaillement du matériau,
• Le moment fléchissant est nul sur appui et maximum en milieu de travée où il vaut . On doit vérifier que les contraintes dans la section à mi-travée ne dépassent ni la résistance à la compression, ni la résistance à la traction du matériau.

Notion de plaque

Notes et références

Articles connexes

• Mécanique
• Matériau
• Essai mécanique
• Statique du solide
• Mécanique statique

Liens externes

• Calculs simples en ligne
• Dates clef de l'histoire de la RdM, Y. Debard
• Logiciel libre pyBar
• Introduction à la résistance des matériaux,
• Calcul statique linéaire pour poutres, Guide de validation des progiciels de calcul de structure, ICAB

• Portail des sciences des matériaux
• Portail de la physique
• Portail du génie mécanique
• Portail du bâtiment et des travaux publics