Point a l'infini

Point a l'infini

Point à l'infini

En mathématiques, dans le sous-domaine de la géométrie projective, le point à l'infini est un point qui peut être ajouté à un corps.

Nombres réels

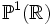Lorsque le point à l'infini est ajouté à la droite des nombres réels, celle-ci forme une courbe fermée, appelée la droite projective réelle, \mathbb P^1(\mathbb{R}).

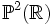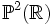Considérons maintenant deux droites parallèles dans le plan projectif \mathbb P^2(\mathbb{R}). Puisque les deux droites sont parallèles, elles se croisent en un point à l'infini. Celui-ci se trouve sur la droite à l'infini dans \mathbb P^2(\mathbb{R}).

De plus, chaque droite est, dans 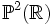\mathbb P^2(\mathbb{R}), une droite projective : chacune à son propre point à l'infini. Deux droites d'un espace affine sont parallèles si et seulement si elles ont le même point à l'infini.

Nombres complexes

Le point à l'infini peut aussi être ajouté au plan complexe 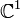\mathbb C^1 afin d'obtenir la droite projective complexe, c'est-à-dire la sphère de Riemann. On peut concevoir ceci en imaginant d'abord le procédé inverse: soit une sphère que l'on perfore. Le trou résultant forme une arête que l'on étire vers l'infini. Ceci forme le plan complexe. En inversant ce procédé, on transforme le plan complexe en droite projective complexe 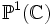\mathbb P^1(\mathbb{C}): le trou est "déperforé" en ajouant le point à l'infini, qui est équivalent à chacun des points sur l'arête qui formait les bords du trou.

Voir aussi

  • Droite à l'infini
  • Hyperplan de l'infini (plan de l'infini)
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Point %C3%A0 l%27infini ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Point a l'infini de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Point à l'infini — ● Point à l infini point de l espace arguésien ou projectif de dimension n, dont la (n + 1)ième coordonnée homogène est nulle …   Encyclopédie Universelle

  • Point à l'infini — En mathématiques, et plus particulièrement en géométrie et en topologie, on appelle point à l infini un objet adjoint à l espace que l on veut étudier pour pouvoir plus commodément y définir certaines notions de limites à l infini , ou encore… …   Wikipédia en Français

  • INFINI — La philosophie a emprunté la notion de l’infini – corrélative de la notion du fini – à la réflexion sur l’exercice de la connaissance, d’une part; à l’expérience ou à la tradition religieuse, de l’autre. Ces deux sources déterminent la variété… …   Encyclopédie Universelle

  • Point ideal — Point à l infini En mathématiques, dans le sous domaine de la géométrie projective, le point à l infini est un point qui peut être ajouté à un corps. Nombres réels Lorsque le point à l infini est ajouté à la droite des nombres réels, celle ci… …   Wikipédia en Français

  • Point idéal — Point à l infini En mathématiques, dans le sous domaine de la géométrie projective, le point à l infini est un point qui peut être ajouté à un corps. Nombres réels Lorsque le point à l infini est ajouté à la droite des nombres réels, celle ci… …   Wikipédia en Français

  • Point de ramification — Point de branchement En analyse complexe, le point de branchement ou point de ramification est un point singulier d une fonction analytique complexe multiforme, telle que la fonction racine n ième ou le logarithme complexe. En ce point s… …   Wikipédia en Français

  • Point (mathématiques) — Point (géométrie) Pour les articles homonymes, voir point …   Wikipédia en Français

  • Point (mathématiques élémentaires) — Point (géométrie) Pour les articles homonymes, voir point …   Wikipédia en Français

  • Point (topologie) — Point (géométrie) Pour les articles homonymes, voir point …   Wikipédia en Français

  • point — 1. point [ pwɛ̃ ] n. m. • 1175 « endroit, moment »; lat. punctum « piqûre », de pungere → poindre I ♦ A ♦ Portion de l espace déterminée avec précision. 1 ♦ Endroit, lieu. En divers, en plusieurs points. « il relevait la tête et fixait son regard …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”