- Point à l'infini
-
En mathématiques, et plus particulièrement en géométrie et en topologie, on appelle point à l'infini un objet adjoint à l'espace que l'on veut étudier pour pouvoir plus commodément y définir certaines notions de limites "à l'infini", ou encore pour obtenir des énoncés plus uniformes, tels que "deux droites se coupent toujours en un point, situé à l'infini si elles sont parallèles".
Sommaire
Introduction
La notion de point à l'infini[1] apparait au XVe siècle dans le cadre du développement des méthodes de la perspective conique, avec l'invention de la « costruzione abbreviata » d'Alberti.
L'utilisation de ces points par les géomètres des XVIe et XVIIe siècles (par exemple Maurolico ou da Vignola en Italie, Stevin en Hollande, Desargues et Pascal en France), puis la systématisation de leur usage au XIXe, a conduit à la création d'une discipline mathématique : la géométrie projective.
La généralisation du langage géométrique dans les mathématiques du XXe siècle, et la possibilité de compactifier les corps des réels et des complexes par l'ajout d'un élément à l'infini a conduit à son tour à l'utilisation de la terminologie « point à l'infini » dans d'autres branches des mathématiques que celles directement dérivées de la géométrie.
Exemples en géométrie projective
La notion de point à l'infini, et plus généralement, d'élément géométrique à l'infini (droite à l'infini, plan à l'infini, hyperplan à l'infini) et leur adjonction à l'ensemble affine considéré, est au cœur de la géométrie projective.
Ainsi, une droite affine à laquelle on ajoute un point à l'infini, forme une droite projective ; un plan affine auquel on ajoute une droite à l'infini forme un plan projectif ; l'espace affine de dimension 3 auquel on ajoute le plan à l'infini (en) forme l'espace projectif de dimension 3.
Ces notions peuvent être généralisées à des dimensions supérieures avec l'introduction de la notion d'hyperplan à l'infini (en), de manière miroir aux notions homologues introduites dans les espaces vectoriels de dimensions finies supérieures à 3.
On peut développer la notion projective de point à l'infini sur tout corps commutatif infini :
- Lorsque le corps de base est
, la droite affine est la droite réelle usuelle. Cette droite augmentée du point à l'infini forme une courbe fermée, appelée « droite projective réelle » et notée 
(voir croquis).
- Lorsque le corps de base est
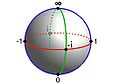
, la droite affine est le plan complexe et la droite projective complexe est la sphère de Riemann 
.
-
La droite projective réelle
est la droite réelle complétée par un point à l'infini. -
La droite projective complexe
est le plan complexe complété par un seul point à l'infini.
- Dans un plan projectif, chaque droite projective a un et un seul point à l'infini. Celui-ci se trouve sur la droite à l'infini du plan projectif. Deux droites projectives ont le même point à l'infini si et seulement si, dans le plan affine, les deux droites affines correspondantes sont parallèles.
Autres exemples
Note
- Pour la variété de la problématique concernant l'usage de l'infini, on pourra consulter l'article infini.
Articles connexes
- Lorsque le corps de base est
Wikimedia Foundation. 2010.
