Point de ramification

Point de ramification

Point de branchement

En analyse complexe, le point de branchement ou point de ramification est un point singulier d'une fonction analytique complexe multiforme, telle que la fonction racine n-ième ou le logarithme complexe. En ce point s'échangent les différentes déterminations.

Géométriquement, cette notion délicate est liée à la surface de Riemann associée à la fonction et relève de la question de la monodromie.

Pour donner une image, cela correspond à un escalier en colimaçon dont l'axe (réduit à un point) est placé à la singularité, desservant plusieurs (voire une infinité) d'étages. Dans le cas d'un nombre fini d'étages, l'escalier a une propriété de périodicité : arrivé au dernier étage, on peut continuer à monter et on se retrouve... au rez-de-chaussée.

En pratique, il suffit de tourner autour d'un point de branchement pour changer d'"étage".

Les différents étages sont appelés des feuillets. L'ordre du point est égal au nombre de feuillets.

Sommaire

Définition

Étant donné une fonction analytique f et un point singulier isolé a , le point a est un point de branchement lorsque l'image par f d'au moins un lacet entourant a est une courbe non fermée. Le point est dit d'ordre n s'il faut au plus n tours autour de a pour refermer la courbe image. Si la courbe ne se referme jamais quel que soit le nombre de tours effectués autour de a, on dit que le point de branchement est transcendant ou logarithmique.

Le point à l'infini peut être un point de branchement pour f(s). Pour le montrer, on considère la fonction f(1/s). Si 0 est un point de branchement de f(1/s) alors l'infini est un point de branchement de f(s).

Développement en un point de branchement d'ordre n

On peut toujours se ramener, par une translation, à considérer que la fonction admet 0 comme point de branchement. Soit f une fonction complexe admettant le point 0 comme point de branchement d'ordre n. La fonction définie par g(s) = f(sn) est alors analytique en 0 : donc pour cette fonction g, le point 0 n'est pas un point de branchement, ce qui implique qu’elle admet un développement de Laurent en 0. On conclut ainsi que f(s) admet un développement en 0 faisant apparaître des puissances non entières. Ces séries sont appelées séries de Puiseux. Par exemple, si l'on cherche le développement de la fonction 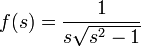f(s)=\frac{1}{s\sqrt{s^2-1}} en s=1, on trouve: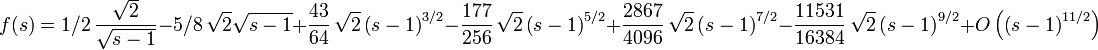

f(s)=1/2\,{\frac {\sqrt {2}}{\sqrt {s-1}}}-5/8\,\sqrt {2}\sqrt {s-1}+{ \frac {43}{64}}\,\sqrt {2} \left( s-1 \right) ^{3/2}-{\frac {177}{256} }\,\sqrt {2} \left( s-1 \right) ^{5/2}+{\frac {2867}{4096}}\,\sqrt {2} \left( s-1 \right) ^{7/2}-{\frac {11531}{16384}}\,\sqrt {2} \left( s- 1 \right) ^{9/2}+O \left( \left( s-1 \right) ^{11/2} \right)

Coupures

Une fonction qui admet un point de branchement en a peut être rendue uniforme en la restreignant à un feuillet particulier de sa surface de Riemann. Pour cela on définit une ligne, appelée coupure, reliant le point a à un autre point de branchement de manière à empêcher que l'on puisse tourner autour de a seul. La fonction ainsi restreinte est alors uniforme, c'est une branche particulière. Lorsque l'on veut faire coïncider les valeurs réelles de la restriction de f à un feuillet avec une fonction classique de la variable réelle (ce qui est courant en physique et dans les sciences de la nature), on choisit une détermination particulière, appelée « branche principale ».

Exemples

  • La fonction "racine n-ième" est une fonction multiforme admettant le point 0 comme point de branchement d'ordre n.
  • La fonction logarithme néperien est également multiforme et admet 0 comme point de branchement d'ordre infini (on dit "point de branchement logarithmique" ou "singularité logarithmique" en ce cas).
  • Soit 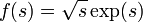f(s) = \sqrt{s}\exp(s). Comment montrer que 0 est un point de branchement ? Pour cela on calcule arg(f(s)). On considère un cercle de rayon r autour de 0. On trouve, posant s = rexp(it), que l'on a 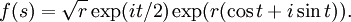f(s) = \sqrt{r}\exp(i t/2) \exp(r (\cos t + i \sin t)). On a donc arg(f(s)) = t / 2 + rsint. Quand t augmente de 2π, on voit que l'argument n'augmente pas d'un multiple de 2π et que f(s) ne retrouve pas sa valeur de départ: 0 est donc un point de branchement pour f (et on peut même dire qu'il s'agit d'un point de branchement d'ordre 2 puisque si t augmente de 4π, f(s) reprend sa valeur initiale, l'argument de f(s) ayant augmenté de 2π).

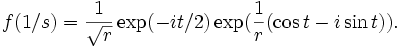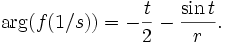Pour le point à l'infini, on calcule de même f(1 / s) et, comme précédemment, on considère un cercle autour de 0 pour s. On a ainsi f(1/s)= \frac1{\sqrt{r}}\exp(-i t /2)\exp(\frac1r(\cos t - i \sin t)). Donc \arg(f(1/s))=- \frac{t}{2} - \frac{\sin t}{r}. Il en résulte que, t augmentant de 2π, f(1 / s) ne reprend pas sa valeur initiale: le point à l'infini pour f(s) est donc un point de branchement (d'ordre 2).

  • Soit f(s) = (Log(s))². Et soit un cercle de rayon r parcouru dans le sens trigonométrique autour de 0 en partant d'un angle t. On a f(r exp(it))= (ln r + it)² = ln²r-t² + 2it ln(r). Quand t augmente de 2 pi, la partie réelle de f diminue de 4 pi² + 4 pi t, et la partie imaginaire augmente de 4 pi ln(r). Pour retrouver le point dont on est parti il faut que la variation de la partie réelle soit égale à 0 ainsi que celle de la partie imaginaire. Pour la partie imaginaire, cela conduit à prendre r=1. Pour la partie réelle, il faut que t=-pi. Donc le seul cercle de centre 0 dont l'image par f soit un cercle est le cercle de rayon 1 parcouru dans le sens trigonométrique à partir de -1. Pour tout autre couple (r,t), le cercle de rayon r centré en 0 ne se referme jamais, même de rayon 1 si l'on le parcourt en partant d'un autre point que -1: le point 0 est donc bien un point de branchement.
  • Si a est un point de branchement pour f, c'est aussi un point de branchement (a priori) pour gof, lorsque g est une fonction entière.

Remarques

  • Le rayon de convergence d'une fonction analytique complexe est limité par une ou plusieurs singularités sur son cercle de convergence. Les points de branchement en font partie.

Exemple: soit 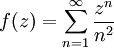f(z)=\sum_{n=1}^{\infty}\frac{z^n}{n^2}. Cette fonction reste bornée partout sur son cercle de convergence |z|=1. Elle ne peut donc pas y admettre un pôle (elle tendrait vers l'infini), ou un point singulier essentiel (pour tout nombre strictement supérieur à π2 / 6, il existerait une suite de points où la somme tendrait vers ce nombre, les points restant de module inférieur à 1, ce qui est impossible). La seule solution est qu'elle y admet un point de branchement. Et effectivement, elle admet le point z=1 comme point de branchement (logarithmique) et comme unique singularité.

  • Un point peut être de branchement dans un feuillet sans l'être dans un autre !

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Point de branchement ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Point de ramification de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Point de branchement — En analyse complexe, le point de branchement ou point de ramification est un point singulier d une fonction analytique complexe multiforme, telle que la fonction racine n ième ou le logarithme complexe. En ce point s échangent les différentes… …   Wikipédia en Français

  • ramification — [ ramifikasjɔ̃ ] n. f. • 1541 anat.; lat. sav. ramificatio 1 ♦ Division en plusieurs rameaux; chacune des divisions ou des rameaux eux mêmes. Ramification d une tige à fleurs. ⇒ inflorescence. Spécialt Ramification des racines, des nervures des… …   Encyclopédie Universelle

  • Ramification — In mathematics, ramification is a geometric term used for branching out , in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign. It is also used from the opposite perspective (branches… …   Wikipedia

  • Ramification — En mathématiques, la ramification est un terme géométrique utilisé au sens de embranchement extérieur, à la façon dont la fonction racine carrée, pour les nombres complexes, peut être vue lorsqu on considère ses deux branches opposées. Il est… …   Wikipédia en Français

  • Weierstrass point — In mathematics, a Weierstrass point P on a nonsingular algebraic curve C defined over the complex numbers is a point such that there are extra functions on C , with their poles restricted to P only, than would be predicted by looking at the… …   Wikipedia

  • Branch point — In the mathematical field of complex analysis, a branch point may be informally thought of as a point z 0 at which a multi valued function (usually referred to as a multifunction in the context of complex analysis) changes values when one winds… …   Wikipedia

  • Polymère ramifié — Illustration d un polymère ramifié Un polymère ramifié (ou branché) est un polymère présentant au moins un point de ramification entre ses deux groupes terminaux, un point de ramification étant un point d une chaîne sur lequel est fixée une… …   Wikipédia en Français

  • noeud — n. m. rI./r d1./d Enlacement étroit obtenu soit en entrecroisant les extrémités d une corde (d un ruban, d un lacet, etc.) puis en tirant sur celles ci, soit en liant une corde (un ruban, etc.) à une ou plusieurs autres. Noeud simple, double.… …   Encyclopédie Universelle

  • RIEMANN (B.) — Après la mort de Georg Friedrich Bernhard Riemann, son œuvre fut publiée en un seul volume, y compris les fragments posthumes, et cette brièveté ne tient pas seulement à la fin précoce du mathématicien: d’une part, ses démonstrations sont très… …   Encyclopédie Universelle

  • nœud — [ nø ] n. m. • 1530; pop. neu 1175; lat. nodus I ♦ Croisement, entrelacement. 1 ♦ Enlacement d une chose flexible (fil, corde, cordage) ou entrelacement de deux objets flexibles, exécuté de façon qu il soit d autant plus serré que l on tire plus… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”