Notation Schoenflies

La notation Schoenflies (ou Schönflies ou Schönfließ), du nom d'Arthur Moritz Schoenflies, est l'une de deux conventions communes utilisées pour décrire les groupes ponctuels de symétrie (aussi appelés groupes cristallographiques). Cette notation est utilisée en spectroscopie. L'autre convention est la notation Hermann-Mauguin, aussi connue sous le nom de notation internationale. Un groupe ponctuel de symétrie dans la convention de Schoenflies est complètement adéquat pour décrire la symétrie de la molécule ; c'est suffisant pour la spectroscopie. Ces deux notations permettent aussi de décrire un groupe d'espace d'un réseau cristallin ; cependant, c'est la notation Hermann-Maunguin qui est utilisée en cristallographie.

Eléments de symétrie

Les éléments de symétrie sont dénotés par i pour les centres de symétrie centrale (ou centres d'inversion dans le langage cristallographique), C pour des axes de rotation, σ pour des plans de réflexion (aussi appelés miroirs) et S pour des axes d'antirotation. C et S sont d'habitude suivis par un indice n pour la notation de l'ordre de rotation possible.

Selon la convention, l'axe de rotation direct de l'ordre le plus grand est défini comme l'axe principal. Tous les autres éléments de symétrie sont décrits par rapport à cela. Ainsi, les miroirs sont dénotés σ_v ou σ_h pour les miroirs verticaux (qui contiennent l'axe principal) et pour les miroirs horizontaux (perpendiculaires à l'axe principal).

Groupe ponctuel de symétrie

En trois dimensions, il y a 32 groupes ponctuels cristallographiques, mais une infinité de groupes ponctuels moléculaires.

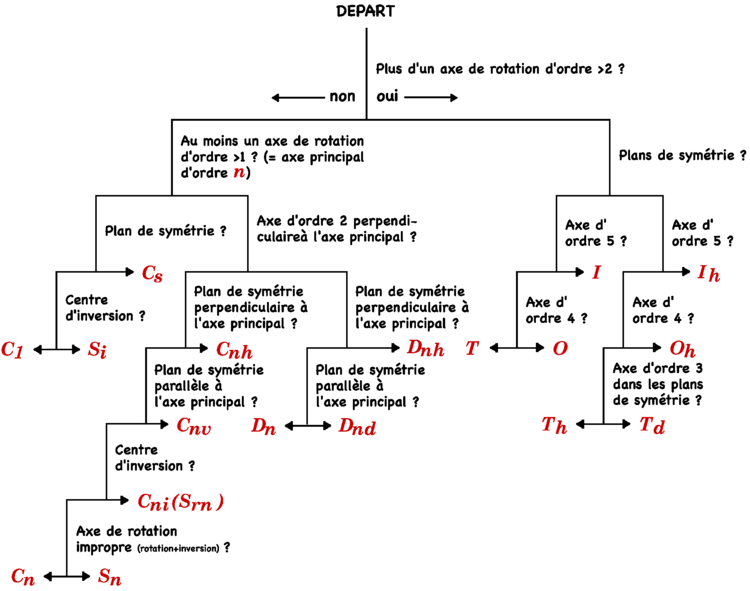
• la lettre I (pour l'icosaèdre (solide platonicien à 20 faces triangulaires et pour le dodécaèdre, 12 faces pentagonales) indique plusieurs axes de rotation d'ordre 5. Si, de plus, il y a des plans de symétries parallèles aux axes d'ordre 5 alors le groupe est I_h.
• La lettre O (pour l'octaèdre) indique que le groupe a la symétrie d'un octaèdre (ou du cube), avec (O_h) ou sans (O) opérations indirectes (qui changent la chiralité).
• La lettre T (pour le tétraèdre) indique que le groupe a la symétrie d'un tétraèdre. T_d inclut des opérations indirectes, T exclut des opérations indirectes et T_h est T avec une inversion.
• C_n (pour groupe cyclique) indique que le groupe contient une rotation d'ordre n. C_nh est C_n avec une réflexion de plan perpendiculaire à l'axe de rotation. C_nv est C_n avec une réflexion de plan parallèle à l'axe de rotation. C_ni est sans aucun plan de symétrie comme C_n mais avec un centre d'inversion. Ce groupe est aussi anciennement noté S_rn car, formellement, un axe de rotation d'ordre n et un centre d'inversion font une roto-inversion d'ordre n (voir ci-dessous).
• S_n (pour Spiegel, allemand de miroir) indique un groupe qui contient seulement une roto-inversion d'ordre n.
• D_n (pour dièdre, ou deux côtés) indique que le groupe contient une rotation d'ordre n plus une rotation d'ordre 2 d'axe perpendiculaire à l'axe de la rotation d'ordre n. D_nh a, de plus, une réflexion de plan perpendiculaire à l'axe de rotation d'ordre n. D_nv a, en plus des éléments de D_n, des réflexions de plans parallèles à l'axe de rotation d'ordre n.

Pour les groupes ponctuels cristallographiques, à cause du théorème de restriction cristallographique, n ne peut prendre que les valeurs 1, 2, 3, 4 et 6 (seules des mailles possédant ces symétries rotationnelles d'ordre n peuvent produire un pavage périodique de l'espace). En revanche, pour des objets comme des molécules, toutes les valeurs de n et même n = ∞ sont possibles. Par exemple, le buckminsterfullerène C₆₀ cristallise dans un groupe d'espace cubique de symétrie ponctuelle T_h, mais la symétrie ponctuelle de la molécule C₆₀ est I_h.

Pour déterminer le groupe de symétrie d'une molécule

Notes et références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Schönflies notation » (voir la liste des auteurs)

Voir aussi

• Théorie des groupes

Liens externes

• Éditions Jacques Gabay, « Œuvres d'Arthur Schoenflies ». Consulté le 6 décembre 2007
• Arthur Schoenflies, « Krystallsysteme und Krystallstructur ». Consulté le 16 avril 2011

• Portail de la physique
• Portail de la chimie
• Portail de la géométrie
• Portail des sciences des matériaux
• Portail des minéraux et roches