Machine de turing

Une machine de Turing est un modèle abstrait du fonctionnement des appareils mécaniques de calcul, tel un ordinateur et sa mémoire, créé par Alan Turing en vue de donner une définition précise au concept d'algorithme ou « procédure mécanique ». Ce modèle^[1] est toujours largement utilisé en informatique théorique, en particulier pour résoudre les problèmes de complexité algorithmique et de calculabilité, on lui adjoint pour cela un oracle.

La thèse Church-Turing postule que tout problème de calcul fondé sur une procédure algorithmique peut être résolu par une machine de Turing. Cette thèse n'est pas un énoncé mathématique, puisqu'elle ne suppose pas une définition précise de procédure algorithmique. En revanche, il est possible de définir une notion de « système acceptable de programmation » et de démontrer que le pouvoir de tels systèmes est équivalent à celui des machines de Turing (Turing-complet).

À l'origine, le concept de machine de Turing, inventé avant l'ordinateur, était censé représenter une personne virtuelle exécutant une procédure bien définie, en changeant le contenu des cases d'un tableau infini, en choisissant ce contenu parmi un ensemble fini de symboles. D'autre part, la personne doit mémoriser un état particulier parmi un ensemble fini d'états. La procédure est formulée en termes d'étapes très simples, du type : « si vous êtes dans l'état 42 et que le symbole contenu sur la case que vous regardez est '0', alors remplacer ce symbole par un '1', passer dans l'état 17, et regarder une case adjacente (droite ou gauche) ».

Sommaire 1 Définition 2 Définition formelle 3 Exemple 4 Machines de Turing universelles 5 Une machine de Turing réelle 6 Notes 7 Voir aussi 7.1 Références et liens externes 7.2 Bibliographie

Définition

La mise en œuvre concrète d'une machine de Turing est réalisée avec les éléments suivants :

1. Un « ruban » divisé en cases consécutives. Chaque case contient un symbole parmi un alphabet fini. L'alphabet contient un symbole spécial « blanc » ('0' dans les exemples qui suivent), et un ou plusieurs autres symboles. Le ruban est supposé être de longueur infinie vers la gauche ou vers la droite, en d'autres termes la machine doit toujours avoir assez de longueur de ruban pour son exécution. On considère que les cases non encore écrites du ruban contiennent le symbole « blanc ».
2. Une « tête de lecture/écriture » qui peut lire et écrire les symboles sur le ruban, et se déplacer vers la gauche ou vers la droite du ruban.
3. Un « registre d'état » qui mémorise l'état courant de la machine de Turing. Le nombre d'états possibles est toujours fini, et il existe un état spécial appelé « état de départ » qui est l'état initial de la machine avant son exécution.
4. Une « table d'actions » qui indique à la machine quel symbole écrire, comment déplacer la tête de lecture ('G' pour une case vers la gauche, 'D' pour une case vers la droite), et quel est le nouvel état, en fonction du symbole lu sur le ruban et de l'état courant de la machine. Si aucune action n'existe pour une combinaison donnée d'un symbole lu et d'un état courant, la machine s'arrête.

Définition formelle

Plusieurs définitions formelles proches les unes des autres peuvent être données d'une machine de Turing. L'une d'elle, relativement courante, est choisie ici.

Une machine de Turing est un septuplet (Q,Σ,Γ,B,q₀,δ,F) où

• Q est un ensemble fini d'états ;
• Σ est l'alphabet des symboles en entrée () ;
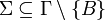• Γ est l'alphabet de travail des symboles de la bande;
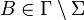• est un symbole particulier (dit blanc) ;
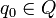• est l'état initial ;
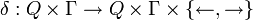• est la fonction de transition ;
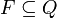• est l'ensemble des états acceptants (ou finaux, terminaux).

Les flèches dans la définition de δ représentent les deux déplacements possibles de la tête de lecture, à savoir le déplacement à gauche et le déplacement à droite. La signification de cette fonction de transition peut être expliquée sur l'exemple suivant : 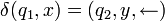signifie que si la machine de Turing est dans l'état q₁ et qu'elle lit le symbole x, elle écrit y à la place de x, va dans l'état q₂, et déplace sa tête de lecture vers la gauche.

Le fonctionnement de la machine de Turing est alors le suivant. A chaque étape de son calcul, la machine évolue en fonction de l'état dans lequel elle se trouve, et du symbole inscrit dans la case du ruban où se trouve la tête de lecture. Ces deux informations permettent la mise à jour de l'état de la machine grâce à la fonction de transition. A l'instant initial, la machine se trouve dans l'état q₀, et le mot inscrit sur le ruban est l'entrée du programme. La machine s'arrête lorsqu'elle rentre dans un état terminal. Le résultat du calcul est alors le mot inscrit sur le ruban.

L'exemple suivant utilise une version très légèrement différente de machine de Turing dans laquelle une machine s'arrête si elle est dans un état terminal, et que le caractère écrit sur le ruban est le bon (ici le blanc).

Exemple

La machine de Turing qui suit possède un alphabet {‘0’, ‘1’}, ‘0’ étant le « blanc ». On suppose que le ruban contient une série de ‘1’, et que la tête de lecture/écriture se trouve initialement au-dessus du ‘1’ le plus à gauche. Cette machine a pour effet de doubler le nombre de ‘1’, en intercalant un ‘0’ entre les deux séries. Par exemple, « 111 » devient « 1110111 ».
L’ensemble d’états possibles de la machine est {e1, e2, e3, e4, e5} et l’état initial est e1.
La table d’actions est la suivante :

Ancien état	Symbole lu	Symbole écrit	Mouvement	Nouvel état
e1	0	(Arrêt)
	1	0	Droite	e2
e2	1	1	Droite	e2
	0	0	Droite	e3
e3	1	1	Droite	e3
	0	1	Gauche	e4
e4	1	1	Gauche	e4
	0	0	Gauche	e5
e5	1	1	Gauche	e5
	0	1	Droite	e1

L’exécution de cette machine pourrait être par exemple (la position de la tête de lecture/écriture sur le ruban est inscrite en caractères gras et rouges) :

Étape État Ruban 1 e1 11 2 e2 01 3 e2 010 4 e3 0100

Étape État Ruban 5 e4 0101 6 e5 0101 7 e5 0101 8 e1 1101

Étape État Ruban 9 e2 1001 10 e3 1001 11 e3 10010 12 e4 10011

Étape État Ruban 13 e4 10011 14 e5 10011 15 e1 11011   (Arrêt)

Le comportement de cette machine peut être décrit comme une boucle :

• Elle démarre son exécution dans l’état e1, remplace le premier 1 par un 0.
• Puis elle utilise l’état e2 pour se déplacer vers la droite, en sautant les 1, et le premier 0 qu’elle rencontre.
• L’état e3 est alors utilisé pour sauter la séquence suivante de 1 (initialement aucun) et remplacer le premier 0 rencontré par un 1.
• e4 permet de revenir vers la gauche jusqu’à trouver un 0, et passer dans l’état e5.
• e5 permet ensuite à nouveau de se déplacer vers la gauche jusqu’à trouver un 0, écrit au départ par l’état e1.
• La machine remplace alors ce 0 par un 1, se déplace d’une case vers la droite et passe à nouveau dans l’état e1 pour une nouvelle itération de la boucle.

Ce processus se répète jusqu’à ce que e1 tombe sur un 0 (c’est le 0 du milieu entre les deux séquences de 1) ; à ce moment, la machine s’arrête.

Machines de Turing universelles

Toute machine de Turing calcule le résultat d'une fonction partielle sur des chaînes de caractères composées des caractères de son alphabet. En ce sens, une machine de Turing se comporte comme un ordinateur avec un programme déterminé.

Mais, comme Alan Turing le décrivit, on peut encoder la table d'actions d'une machine de Turing sous la forme d'une chaîne de caractères. On peut donc tenter de construire une machine de Turing qui suppose l'existence sur son ruban d'une chaîne de caractères encodant une table d'actions, suivie d'une chaîne de caractères constituant les données effectives du ruban, et calcule le contenu du ruban que la machine de Turing encodée aurait calculé.

Comme Alan Turing le montra dans son article fondateur, il est possible de créer une telle machine de Turing et puisqu'elle peut simuler le comportement de n'importe quelle autre machine de Turing, on l'appelle « machine de Turing universelle ».

Grâce à cet encodage des tables d'actions sous forme de chaînes de caractères, il devient en principe possible que les machines de Turing répondent à des questions à propos du comportement d'autres machines de Turing. Cependant, la plupart de ces questions sont indécidables, c'est-à-dire que la fonction en question ne peut pas être calculée par une machine de Turing.
Par exemple, la question de savoir si une machine de Turing atteint à un moment donné un état d'arrêt ou ne l'atteint jamais pour une entrée particulière, ou pour toutes les entrées possibles, connue sous le nom de problème de l'arrêt, fut démontré comme étant indécidable par Turing. Le théorème de Rice montre que toute proprieté non triviale sur le langage acceptée par une machine de Turing est indécidable.

Si on élargit la définition pour y inclure les machines de Turing qui simulent des modèles de calcul Turing-complets, et non plus seulement les machines de Turing qui simulent directement d'autres machines de Turing, une machine de Turing universelle peut être relativement simple, et utiliser seulement quelques états et symboles. Par exemple, il existe une machine de Turing universelle de taille 2×18 (c'est-à-dire 2 états, et 18 symboles).
Les plus petites machines de Turing universelles connues ont les tailles suivantes : 2×18, 3×10, 4×6, 5×5, 7×4, 10×3, 22×2. Ces dernières simulent un modèle appelé tag system.

Une machine de Turing de taille 2×3 proposée par Stephen Wolfram, a été annoncée comme la plus petite machine de Turing universelle ^[2]. La preuve est due à Alex Smith. Cependant la notion d'universalité utilisée dans cette preuve n'est pas la même que celle décrite informellement ci-dessus. En particulier, elle nécessite d'écrire une infinité de symboles initialement sur le ruban pour préparer le calcul.

Une machine de Turing universelle est Turing-complète. Elle peut calculer toute fonction récursive, analyser tout langage récursif, et accepter tout langage partiellement décidable. Selon la thèse de Church-Turing, les problèmes résolubles par une machine de Turing universelle sont exactement les problèmes résolubles par un algorithme ou par une méthode concrète de calcul, en supposant une définition raisonnable de ces termes.

Une machine de Turing réelle

Il est assez aisé de simuler une machine de Turing sur un ordinateur moderne, jusqu'au moment où la mémoire de l'ordinateur devient éventuellement pleine (si la machine de Turing utilise une très grande partie du ruban) !

Il est aussi possible de construire une machine de Turing purement mécanique. Le mathématicien Karl Scherer en construisit une en 1986 en utilisant des jeux de construction en métal et en plastique, et du bois. Sa machine, haute d'un mètre et demi utilise des ficelles pour lire, déplacer et écrire les données (représentées à l'aide de roulements à billes)^{[réf. souhaitée]}.

La machine est actuellement exposée dans le hall du département d'informatique de l'Université d'Heidelberg en Allemagne.

De même, en utilisant environ 300 miroirs, il est possible de créer une machine de Turing universelle optique en utilisant la méthode dite du fer à cheval conçue par Stephen Smale^{[réf. souhaitée]}.

Notes

Voir aussi

• Machine de Turing non-déterministe
• Machine de Blum-Shub-Smale : une généralisation à des machines calculant sur

Références et liens externes

• (fr) O. Carton, Langages formels, calculabilité et complexité. Vuibert 2008, ISBN 978-2-7117-2077-4
• (fr) J.-M. Autebert, Calculabilité et décidabilité. Dunod 1992, ISBN 978-2225826320
• (fr) Machine de Turing, une applet java simulant des machines de Turing .
• (en) JFLAP, un outil de simulation de machines de Turing et de manipulation d'automates (déterminisation, minimisation, etc)
• (en) Turing Machine Simulator, un simulateur de machine de Turing en applet Java.
• (fr) É. Jacopin, Les machines de Turing -- Introduction à la caractérisation de la complexité d'un problème. Cépaduès 2009, ISBN 978-2-85428-865-0

Bibliographie

• Alan Turing, Jean-Yves Girard, La machine de Turing, 1995 [détail des éditions] 

Cet ouvrage comprend notamment une traduction en français (par Julien Basch et Patrice Blanchard) de l'article original, ainsi qu'une correction par Emil Post des erreurs y figurant :

• (en) Alan Mathison Turing, On Computable Numbers, with an Application to the Entscheidungsproblem, vol. 2:42, coll. « Proceedings of the London Mathematical Society », 1936, p. 230-265 

Informatique théorique
Théorie du calcul	Calculabilité Décidabilité et indécidabilité • Ensemble récursif • Problème de l'arrêt • Récursivement énumérable Modèle de calcul Automate fini • Automate cellulaire • Machine de Turing • Thèse de Church Modes de calcul Concurrence • Parallèlisme • Théorie de l'ordonnancement Mesure et échelle de complexité Réduction polynomiale • Problème NP-complet
Logique, syntaxe et sémantique	Logique mathématique Assistant de preuve • Calcul des prédicats • Correspondance de Curry-Howard • Fonction récursive • Lambda-calcul • Théorème d'incomplétude de Gödel • Théorie des types Grammaire formelle et systèmes de réécriture Compilation • Expression rationnelle • Grammaire formelle • Langage rationnel • Théorie des langages Sémantique Sémantique des langages de programmation • Sémantique dénotationnelle • Sémantique axiomatique • Sémantique opérationnelle Spécifier, vérifier et concevoir des programmes Interprétation abstraite • Méthodes formelles • Model checking
Algorithmique, complexité et mathématiques discrètes	Algorithmique Algorithme génétique • Algorithme glouton • Algorithme probabiliste • Complexité algorithmique • Diviser pour régner • Heuristique • Programmation dynamique Problèmes et algorithmes numériques Algorithme du simplexe • Géométrie algorithmique • Algorithme d'Euclide • Test de primalité Problèmes et algorithmes non-numériques Algorithmes de la théorie des graphes • Arbre (informatique) • Liste (informatique) • Table de hachage • Tas (informatique) Théorie des graphes Coloration de graphe • Problèmes de cheminement Recherche opérationnelle Optimisation • Optimisation combinatoire • Théorie de l'ordonnancement Données et codage Codage • Codage de l'information • Compression de données • Cryptage • Cryptanalyse • Cryptographie • Théorie de l'information

• Portail des mathématiques
• Portail de l’informatique