Tas (informatique)

Pour les articles homonymes, voir Tas.

Un exemple de tas

En informatique, un tas, en anglais heap, (ou plus précisément un tas binaire) est une structure de données répondant aux conditions suivantes :

• c'est un arbre binaire complet
• il est ordonné en tas

Description

On dit qu'un arbre est ordonné en tas lorsque la propriété suivante est vérifiée : les nœuds sont ordonnés par leurs clés respectives, et :

Pour tout nœuds A et B de l'arbre tels que B soit un fils de A 
   clé(A) ≥ clé(B)

ou

Pour tout nœuds A et B de l'arbre tels que B soit un fils de A 
   clé(A) ≤ clé(B)

Un arbre vérifiant cette propriété est aussi appelé "arbre tournoi". Cette propriété implique que la plus grande clé (ou la plus petite) soit située à la racine du tas. Ils sont ainsi très utilisés pour implémenter les files à priorités car ils permettent des insertions en temps logarithmique et un accès direct au plus grand élément. L'efficacité des opérations effectuée sur des tas est très importante dans de nombreux algorithmes sur les graphes.

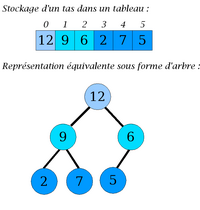
Le fait qu'un tas soit un arbre binaire complet permet de le représenter d'une manière intuitive par un tableau unidimensionnel.

• Tableau indicé à partir de 0 : le père d'un nœud en position i a pour position , et donc les enfants d'un nœud en position i sont situés à 2i+1 et 2i+2.
• Tableau indicé à partir de 1 : le père d'un nœud en position i a pour position , et donc les enfants d'un nœud en position i sont situés à 2i et 2i+1.

Les tas sont en outre utilisés dans l'algorithme de tri par tas.

Remarques

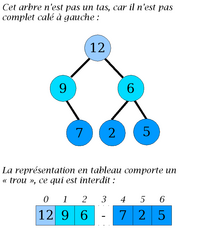
• Les multiples définitions existantes pour « arbre complet » peuvent porter à confusion. Ici, il est important que les nœuds de l'arbre puissent être stockés de façon contiguë dans un tableau. Donc, tous les étages, de la racine jusqu'à l'avant-dernier, doivent obligatoirement être remplis. De plus, les feuilles de la dernière ligne doivent être "calées à gauche". En revanche, un tas pouvant avoir un nombre quelconque d'éléments, il n'est pas obligatoire que la dernière ligne soit complètement remplie.
• La notion de plus grande clé est équivalente à la notion de plus petite clé, seule diffère la relation d'ordre total utilisée. Les algorithmes restent donc les mêmes si l'on veut accéder directement au plus petit élément et non au plus grand. On peut même, dans la plupart des langages de programmation modernes, programmer de façon à passer la relation d'ordre désirée en paramètre des algorithmes de construction et de manipulation de tas.

Attention : un tas est organisé selon une seule relation d'ordre à la fois. Il faut donc décider dès sa construction si l'on veut accéder ensuite au plus grand élément, ou au plus petit, et selon quel attribut de l'objet stocké dans l'étiquette de chaque nœud. Les manipulations suivantes de ce tas devront obligatoirement se faire par rapport à la même relation d'ordre.

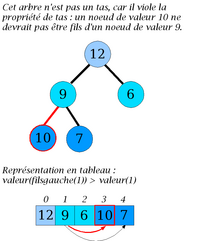
Contre-exemples

Les deux contre-exemples suivants ont pour relation d'ordre :

Contre-exemple n°1

Contre-exemple n°2

Primitives

Les Tas supportent les opérations suivantes :

• Construire-Tas
• Ajouter-Élément
• Consulter-Sommet
• Retirer-Élément
• Tamiser
• Tri-Par-Tas

Selon les implémentations, les primitives Ajouter-Élément et Retirer-Élément invalident la propriété de Tas, ou bien appellent la procédure Tamiser pour le réorganiser.

Souvent Retirer-Élément n'est appelée que pour retirer le sommet.

Voir aussi

Articles connexes

• Tas binomial
• Tas de Fibonacci

• Portail de la programmation informatique
• Portail de l'informatique théorique