Machine De Turing Non Déterministe

Présentation intuitive

Alors qu'une machine de Turing normale (déterministe), connaissant le caractère lu sur le ruban et l'état courant, a au plus un choix pour passer dans l'état suivant, une machine de Turing non déterministe en a plusieurs.

Ce qui signifie qu'alors qu'une machine de Turing déterministe effectue une série de calculs, une machine de Turing non déterministe effectue un arbre de calculs, chaque chemin de cet arbre correspondant à une série de calculs possibles.

On peut imaginer qu'une machine de Turing non déterministe arrivée à un état où il y a plusieurs états suivants possibles, se divise, elle-même et son ruban, et que chaque sous-machine va dans un état différent.

Cette description permet facilement de voir qu'une vraie machine de Turing non déterministe, qui peut effectuer un nombre illimité de calculs en parallèle en autant de temps qu'il en faudrait pour résoudre un seul calcul n'est pas constructible dans le monde réel (nous ne pouvons construire que des machines de Turing déterministes). La machine de Turing non déterministe est donc un outil théorique. Il est toutefois possible de construire des machines qui, face à plusieurs possibilités de choisir l'état suivant, en choisissent un arbitrairement. Nous obtenons ainsi une machine qui donne un seul résultat à la fois, mais ce ne sera pas forcément toujours le même si on exécute le traitement plusieurs fois à la suite.

Description formelle

• Q est un ensemble fini d'états.
• Σ est l'alphabet, un ensemble fini de symboles.
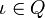• est l'état initial.
• est le symbole blanc()
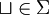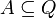• est l'ensemble des états "acceptants", ou finaux.
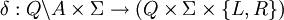• est une fonction multivaluée sur les états et les symboles. C'est la fonction de transition. L est le décalage à gauche et R est le décalage à droite.

Dans une machine de Turing ordinaire, la fonction de transition n'est pas multi-valuée.

Résultat d'une machine de Turing non déterministe

Supposons qu'une machine de Turing doit résoudre un problème de décision. Il se peut que, devant un ruban donné:

• certains chemins de calcul se terminent avec une réponse OUI.
• certains autres se terminent avec une réponse NON.
• certains autres ne se terminent jamais.

La question de savoir quelle est la réponse fournie par la machine pose donc problème.

Lien avec la théorie de la complexité

D'après l'une des définitions possibles, un problème de complexité NP est un problème qui peut être décidé en temps polynomial par une machine de Turing non déterministe.

Voir aussi

• Machine de Turing
• Automate fini
• Théorie des langages
• Langage formel
• Théorie de la complexité des algorithmes