Machine d'état

Un automate fini (on dit parfois machine à états finie), en anglais finite state automaton ou finite state machine (FSA, FSM), est une machine abstraite utilisée en théorie de la calculabilité et dans l'étude des langages formels. C'est un outil fondamental en Informatique, où il intervient notamment en compilation des langages informatiques (procédé permettant de passer d'un langage de haut niveau en langage machine binaire).

Un automate est constitué d'états et de transitions. Son comportement est dirigé par un mot fourni en entrée : l'automate passe d'état en état, suivant les transitions, à la lecture de chaque lettre de l'entrée. L'automate est dit « fini » car il possède un nombre fini d'états distincts : il ne dispose donc que d'une mémoire bornée.

Un automate fini forme un graphe orienté étiqueté, dont les états sont les sommets et les transitions les arêtes étiquetées.

Sommaire 1 Utilisation 2 Définitions formelles 2.1 Automate fini déterministe 2.2 Automate fini non déterministe 2.3 Automate fini non déterministe généralisé 3 Exemples de machines à états finis 3.1 machine à états finie déterministe 4 Langages rationnels et langages reconnaissables 5 Optimisation et mise sous forme canonique 6 Puissance informatique 7 Représentation 8 Exécution 9 Voir aussi 9.1 Articles connexes 9.2 Références 9.3 Liens externes

Utilisation

Il existe plusieurs types de machines à états finie. Les « accepteurs » produisent en sortie une réponse « oui » ou « non », c'est-à-dire qu'ils acceptent (oui) ou rejettent (non) l'entrée. Les systèmes de reconnaissance classent l'entrée par catégorie. Enfin, les capteurs sont employés pour produire un certain résultat en fonction de l'entrée.

Les automates finis peuvent caractériser des langages (c'est-à-dire, des ensembles de mots) finis (le cas standard), des langages de mots infinis (automates de Rabin, automates de Büchi), ou encore divers types d'arbres (automates d'arbres).

Une autre distinction est faite entre les automates déterministes et les non déterministes (qu'il conviendrait mieux de qualifier de « nondéterministes »). Un automate est déterministe si, pour chacun de ses états, il y a au plus une transition pour chaque étiquette possible. S'il y en a exactement une, on parle alors d'automate déterministe complet. Dans les automates non déterministes, il peut y avoir un nombre quelconque de transitions à partir d'un état donné pour une étiquette donnée. Ici, le terme « non déterministe » n'est pas la négation de « déterministe ».

Un automate fini non déterministe est toujours transformable en un automate fini déterministe équivalent. Dans le pire des cas, l'automate déterministe produit est exponentiellement plus grand (en nombre d'états) que l'automate non déterministe, mais il est en général possible d'en diminuer considérablement le nombre d'états.

Indépendamment de la théorie, les machines à états finis se rencontrent également dans les circuits digitaux, où l'entrée, l'état et le résultat sont des vecteurs de bits de taille fixe (machines de Moore et machines de Mealy). Dans les machines de Mealy, les actions (sorties) sont liées aux transitions, tandis que dans les machines de Moore, les actions sont liées aux états.

Définitions formelles

Automate fini déterministe

Un automate fini déterministe (AFD) A est un quintuplet A = (E,Σ,t,i,Q) où :

• E est un ensemble fini d'états,
• Σ est un alphabet, c'est-à-dire un ensemble de lettres,
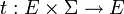• est une fonction de transition,
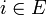• est l'état de départ ou état initial,
• et 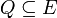est un ensemble d'états « accepteurs » ou états terminaux.

L'automate prend un mot (constitué de symboles de son alphabet) en entrée et démarre dans son état initial. Il parcourt ensuite le mot en utilisant la fonction de transition t afin de déterminer, pour chaque lettre, le prochain état à parcourir en utilisant l'état courant et le symbole venant d'être lu.

Si, à la fin de la lecture, la machine est dans un état accepteur, on dit qu'elle accepte l'entrée. Autrement, on dit qu'elle la rejette.

L'ensemble des entrées acceptées forme un langage L, qui est le langage « reconnu » par l'automate A. On dit que « A reconnaît le langage L ». Autrement dit, A reconnaît tous les mots de L, et A refuse tous les mots de Σ* (* désigne l'étoile de Kleene) qui ne sont pas dans L.

Un automate de Büchi déterministe opère sur des mots infinis. Un mot infini est accepté si l'automate de Büchi passe un nombre infini de fois par les états acceptants lorsqu'il lit ce mot.

Automate fini non déterministe

Un automate fini non déterministe (AFN) A est un quintuplet A = (E,Σ,t,I,Q) où :

• E est un ensemble fini d'états,
• Σ est un alphabet,
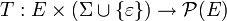• est une fonction de transition,
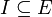• est un ensemble non vide d'états initiaux,
• et 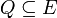est un ensemble d'états terminaux.

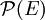est l'ensemble des parties de E (aussi noté 2^E) et est la séquence de taille nulle, aussi appelée « mot vide ».

La machine A démarre dans l'état de départ et reçoit en entrée une séquence w de symboles de son alphabet. Elle emploie la relation de transition T pour déterminer le ou les prochains états atteignables en utilisant les états actuellement atteignables et le symbole venant d'être lu. On dit que l'automate non déterministe A accepte l'entrée w si un des états accepteurs est atteignable au terme de la lecture de l'entrée, c'est-à-dire s'il existe au moins un parcours des états de l'automate tel qu'à la fin la tête de lecture arrive sur un état terminal. Sinon, A rejette w.

L'ensemble des entrées acceptées forme un langage dénoté généralement par L(A).

Automate fini non déterministe généralisé

Un automate fini non déterministe généralisé (AFNG) A est un quintuplet (E,Σ,t,I,q) où :

• E est un ensemble d'états,
• Σ est un alphabet,
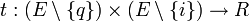• est une fonction de transition,
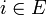• est l'état initial,
• et 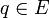est l'état accepteur.

R est l'ensemble de toutes les expressions rationnelles sur l'alphabet Σ.

Un AFD ou un AFN peut facilement être converti en AFNG et alors l'AFNG peut être facilement converti en expression rationnelle en réduisant le nombre d'états jusque à ce que E = {s,a}.

Exemples de machines à états finis

machine à états finie déterministe

L'exemple suivant décrit une machine à états finie déterministe sur un alphabet binaire, qui détermine si l'entrée contient un nombre pair de 0.

A = (E,Σ,t,i,Q)

• E = {E₁,E₂}
• Σ = {0,1}
• i = E₁
• Q = {E₁}
• La fonction de transition t est définie comme suit :
  • t(E₁,0) = E₂
  • t(E₁,1) = E₁
  • t(E₂,0) = E₁
  • t(E₂,1) = E₂

Si lors du parcours d'une entrée, on se trouve à l'état E₁, cela signifie qu'il y a eu un nombre pair de 0 dans l'entrée jusqu'à présent, si on se trouve à l'état E₂, cela signifie qu'il y en a eu un nombre impair. Un 1 dans l'entrée ne change pas l'état de l'automate. Quand l'entrée finit, l'état montrera si l'entrée a contenu un nombre pair de 0 ou pas.

Langages rationnels et langages reconnaissables

Stephen Kleene a démontré que les langages reconnus par les automates finis sont exactement les langages qui peuvent être décrits par les expressions rationnelles. En d'autres termes, pour toute expression rationnelle, on peut construire un automate fini (déterministe ou non) qui reconnaisse cette expression ; de même, pour tout automate fini (déterministe ou non), on peut exprimer sous forme d'une expression rationnelle le langage qu'il reconnaît.

Optimisation et mise sous forme canonique

Optimiser ou minimiser un automate fini, c'est-à-dire calculer l'automate avec le plus petit nombre d'états et qui reconnait le même langage, est un problème décidable, à la différence de problèmes similaires pour des machines informatiques plus puissantes. En outre, il est possible de construire une version canonique de n'importe quel automate fini, afin de déterminer l'égalité de deux automates.

Ces deux problèmes peuvent être résolus en utilisant un algorithme de coloriage.

Puissance informatique

Les machines à états finis peuvent uniquement identifier des langages rationnels, et par conséquent elles sont moins puissantes que les machines de Turing. Il existe des problèmes que l'on peut décider mais qui ne sont pas calculables en utilisant une machine à états finie.

Pour chaque machine non déterministe ayant n états, une machine déterministe de puissance égale peut être construite avec un algorithme. Cette machine déterministe a dans le pire des cas un nombre d'états égal au nombre de parties de l'ensemble des états de la machine initiale, c’est-à-dire 2ⁿ.

Représentation

Une machine à états finie peut être représentée en utilisant une table de transition d'état ou un diagramme d'état.

Exécution

Une machine à états finie peut être implémentée sous forme logicielle avec une matrice de transition d'état.

Dans certains cas, il est plus avantageux d'utiliser une matrice creuse implémentée avec des listes liées ou un énorme switch pour détecter l'état interne et puis les différents switchs plus petits pour décoder le symbole d'entrée.

Une machine à états finie peut aussi être implémentée sous forme matérielle avec un dispositif de logique programmable.

Enfin, une manière plus élégante et plus souple est d'implémenter le patron de conception state si le langage s'y prête.

Voir aussi

Articles connexes

• Théorie des automates
• Automate à pile
• Automate d'arbres

Références

• (fr) Jacques Sakarovitch, Eléments de théorie des automates, Vuibert 2003. (ISBN 978-2-7117-4807-5).
• (fr) Olivier Carton, Langages formels, calculabilité et complexité. Vuibert 2008, (ISBN 978-2-7117-2077-4).

Liens externes

• Théorie des langages par Francois Yvon et Akim Demaille

Informatique théorique
Théorie du calcul	Calculabilité Décidabilité et indécidabilité • Ensemble récursif • Problème de l'arrêt • Récursivement énumérable Modèle de calcul Automate fini • Automate cellulaire • Machine de Turing • Thèse de Church Modes de calcul Concurrence • Parallèlisme • Théorie de l'ordonnancement Mesure et échelle de complexité Réduction polynomiale • Problème NP-complet
Logique, syntaxe et sémantique	Logique mathématique Assistant de preuve • Calcul des prédicats • Correspondance de Curry-Howard • Fonction récursive • Lambda-calcul • Théorème d'incomplétude de Gödel • Théorie des types Grammaire formelle et systèmes de réécriture Compilation • Expression rationnelle • Grammaire formelle • Langage rationnel • Théorie des langages Sémantique Sémantique des langages de programmation • Sémantique dénotationnelle • Sémantique axiomatique • Sémantique opérationnelle Spécifier, vérifier et concevoir des programmes Interprétation abstraite • Méthodes formelles • Model checking
Algorithmique, complexité et mathématiques discrètes	Algorithmique Algorithme génétique • Algorithme glouton • Algorithme probabiliste • Complexité algorithmique • Diviser pour régner • Heuristique • Programmation dynamique Problèmes et algorithmes numériques Algorithme du simplexe • Géométrie algorithmique • Algorithme d'Euclide • Test de primalité Problèmes et algorithmes non-numériques Algorithmes de la théorie des graphes • Arbre (informatique) • Liste (informatique) • Table de hachage • Tas (informatique) Théorie des graphes Coloration de graphe • Problèmes de cheminement Recherche opérationnelle Optimisation • Optimisation combinatoire • Théorie de l'ordonnancement Données et codage Codage • Codage de l'information • Compression de données • Cryptage • Cryptanalyse • Cryptographie • Théorie de l'information

• Portail de l’informatique