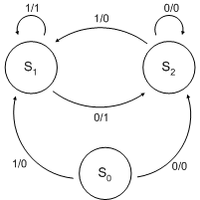
Machine de Mealy

Machine de Mealy
Le diagramme états-transitions d'une machine de Mealy simplifiée.


En théorie de la calculabilité, une machine de Mealy ou automate de Mealy est un automate fini (et plus précisément un transducteur à état fini) pour lequel les valeurs des variables de sortie dépendent à la fois de l'état courant et des variables d'entrée. Cela signifie que le diagramme états-transitions inclura à la fois un signal d'entrée et un signal de sortie pour chaque transition. Cette définition s'oppose à celle des machines de Moore pour lesquelles les valeurs en sortie ne dépendent que de l'état courant. Cependant, il existe pour chaque machine de Mealy, une machine de Moore équivalente.

Cet automate tient son nom de G. H. Mealy, qui proposa ce modèle en 1955[1].

Sommaire

Définition formelle

Une machine de Mealy est un 6-uplet, (S, S0, Σ, Λ, T, G), constitué de :

  • un nombre fini d'états S ;
  • un état initial S0, où S0 \in S ;
  • un ensemble fini Σ, appelé alphabet d'entrée ;
  • un ensemble fini Λ, appelé alphabet de sortie ;
  • une fonction de transition T : S × Σ → S ;
  • une fonction de sortie G : S × Σ → Λ.

Applications

Les machines de Mealy fournissent un modèle mathématique rudimentaire pour représenter le chiffrement des informations.

Supposons que l'alphabet d'entrée et l'alphabet de sortie soient l'ensemble des chaînes de caractères latins. Il est possible de concevoir une machine de Mealy transformant une chaîne de caractères en clair (entrée) en une chaîne chiffrée (sortie).

Cet exemple est toutefois théorique, car s'il est possible de décrire Enigma (par exemple) en utilisant une machine de Mealy, le diagramme états-transitions en serait trop complexe pour une interprétation efficace.

Voir aussi

Notes et références

  1. ↑ Mealy, G.H. (September 1955). "A Method for Synthesizing Sequential Circuits". Bell System Tech. J. 34: 1045–1079.

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Machine de Mealy de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Mealy machine — In the theory of computation, a Mealy machine is a finite state machine whose output values are determined both by its current state and the current inputs. The outputs change asynchronously with respect to the clock, meaning that the outputs… …   Wikipedia

  • Machine de Moore — Le diagramme états transitions d une machine de Moore dont les entrées sont x, y, z, et les sorties a, b, c. En théorie de la calculabilité, une machine de Moore (inventée par Edward F. Moore) est un automate fini pour lequel les valeurs des… …   Wikipédia en Français

  • Machine d'état — Automate fini Pour les articles homonymes, voir Automate. Exemple d un diagramme d automate fini. Un automate fini (on dit parfois machine …   Wikipédia en Français

  • Machine à états finis — Automate fini Pour les articles homonymes, voir Automate. Exemple d un diagramme d automate fini. Un automate fini (on dit parfois machine …   Wikipédia en Français

  • Finite-state machine — State machine redirects here. For infinite state machines, see State transition system. For fault tolerance methodology, see State machine replication. SFSM redirects here. For the Italian railway company, see Circumvesuviana. A finite state… …   Wikipedia

  • Finite state machine — A finite state machine (FSM) or finite state automaton (plural: automata ) or simply a state machine, is a model of behavior composed of a finite number of states, transitions between those states, and actions. A finite state machine is an… …   Wikipedia

  • Moore machine — In the theory of computation, a Moore machine is a finite state machine, whose output values are determined solely by its current state.  Contents 1 Name 2 Formal definition 3 Visual representation …   Wikipedia

  • Finite-State-Machine — Abb.1 Beispiel eines EA Ein endlicher Automat (EA, auch Zustandsmaschine, englisch finite state machine (FSM)) ist ein Modell des Verhaltens, bestehend aus Zuständen, Zustandsübergängen und Aktionen. Ein Automat heißt endlich, wenn die Menge der… …   Deutsch Wikipedia

  • Finite State Machine — Abb.1 Beispiel eines EA Ein endlicher Automat (EA, auch Zustandsmaschine, englisch finite state machine (FSM)) ist ein Modell des Verhaltens, bestehend aus Zuständen, Zustandsübergängen und Aktionen. Ein Automat heißt endlich, wenn die Menge der… …   Deutsch Wikipedia

  • State machine replication — Introduction from Schneider s 1990 survey: : Distributed software is often structured in terms of clients and services. Each service comprises one or more servers and exports operations that clients invoke by making requests. Although using a… …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”