- Intégration numérique
-
Calcul numérique d'une intégrale
En analyse numérique, il existe toute une famille d'algorithmes permettant d'approcher la valeur numérique d'une intégrale. Toutes consistent à approcher l'intégrale
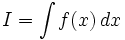 par une formule dite de quadrature, du type
par une formule dite de quadrature, du type 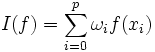 . Le choix de p, des pondérations ωi et des nœuds xi dépendent de la méthode employée. Il conviendra aussi de s'intéresser à la précision des formules utilisées.
. Le choix de p, des pondérations ωi et des nœuds xi dépendent de la méthode employée. Il conviendra aussi de s'intéresser à la précision des formules utilisées.Une première indication de l'efficacité d'une méthode est donnée par son ordre. Par définition, une méthode de quadrature est d'ordre n quand elle donne la valeur exacte de l'intégrale pour tout polynôme de degré inférieur ou égal à n, et un résultat faux pour au moins un polynôme de degré n+1.
Sommaire
Méthode de calcul d'intégrale à une dimension
Ces méthodes utilisent l'interpolation des fonctions à intégrer. Généralement, les fonctions sont interpolées par des polynômes dont on connait facilement la primitive.
Formules simples
Formules du rectangle et du point milieu
C'est la méthode la plus simple qui consiste à interpoler la fonction f à intégrer par une fonction constante (polynôme de degré 0). Soit ξ le point d'interpolation; la formule devient alors:
Le choix du point a de l'importance pour la détermination du terme d'erreur
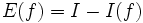 :
:- Si
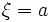 ou
ou 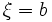 , l'erreur est
, l'erreur est ![E(f) = \frac{(b-a)^2}{2} f'(\eta), \quad \eta \in [a,b]](/pictures/frwiki/51/31624fd22d02a54dda441e6106865f6f.png) . C'est la méthode du rectangle;
. C'est la méthode du rectangle; - Si
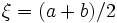 , alors l'erreur devient
, alors l'erreur devient ![E(f) = \frac{(b-a)^3}{24} f''(\eta), \quad \eta \in [a,b]\,](/pictures/frwiki/51/3b57e4a3754769ca80634b9ae4daf463.png) . Il s'agit de la méthode du point milieu.
. Il s'agit de la méthode du point milieu.
Ainsi, le choix du point milieu améliore l'ordre de la méthode. La méthode du rectangle est exacte (c'est-à-dire E(f) = 0) pour les fonctions constantes et celle du point milieu est exacte pour les polynômes de degré inférieur ou égal à 1. Ceci s'explique par le fait que pour l'intégration de x, la méthode du point milieu donne lieu à deux erreurs d'évaluation, égales en valeur absolue et opposées en signe.
Formule du trapèze
Si on interpole f par un polynôme de degré un (fonction affine), on a besoin de deux points d'interpolation, à savoir (a, f(a)) et (b, f(b)). L'intégrale est alors approchée par l'aire du polynôme interpolateur, en l'occurrence un trapèze. Ceci justifie le nom de méthode des trapèzes:
L'erreur commise est
L'erreur s'annule pour tout polynôme de degré inférieur ou égal à un. Selon ce critère, la méthode des trapèzes est donc moins performante que celle du point milieu, étant donné que les degrés d'exactitude sont les mêmes et qu'il y a une évaluation de plus avec la méthode des trapèzes.
Formule de Simpson
La fonction f est maintenant remplacée par une parabole, qui nécessite trois points d'interpolation. Les extrémités a, b, et leur milieu m sont choisis. La méthode de Simpson consiste alors à remplacer l'intégrale par
L'erreur est
Le degré d'exactitude est de 3 pour cette méthode, pour 3 évaluations de f.
Le tableau suivant résume les performances de chaque méthode
Nom de la
MéthodeDegré du
polynomeNombre de
pointsDegré
d’exactitudeDegré
d’erreurCoefficient
d’erreurRectangle 0 1 0 2 1/2 Point Milieu 0 1 1 3 1/24 Trapèze 1 2 1 3 -1/12 Simpson 2 3 3 5 -1/2880 Les formules de Newton-Cotes permettent de généraliser ces résultats sur des intervalles constants, où la fonction f est interpolée par des polynômes de degré de plus en plus élevé. Pour des questions de stabilité numérique, il est préferable de limiter le degré du polynôme d'interpolation en subdivisant l'intervalle en sous-intervalles, pour lesquels une interpolation linéaire est suffisante.
Formules composites
Pour chacune des méthodes précédentes, le terme d'erreur dépend de b-a. Si cette amplitude est trop élevée, on peut réduire simplement l'erreur en découpant l'intervalle [a, b] en n sous-intervalles, sur lesquels on calculera la valeur approchée de l'intégrale. On parle alors de formule composite. La valeur sur l'intervalle [a, b] sera la somme de la valeur sur chaque sous-intervalle.
Pour la méthode du point milieu, la formule devient
où mk est le milieu du k-ième sous-intervalle. Puisque les n sous-intervalles sont identiques, ils sont de la forme [a + k h, a + (k+1) h], avec h = (b-a)/n et k = 0, 1, 2, ..., n-1. Ceci entraîne finalement que mk = a + kh + h / 2. Le terme d'erreur s'écrit
![E(h)= h^2 \frac{(b-a)}{24} f''(\eta),\quad \eta\in [a,b]](/pictures/frwiki/99/cbc21aec938ecf109a61471de0c2535a.png) . La formule composite a un ordre 1, comme précédemment. L'agrégation a fait baisser d'une puissance le terme en (a-b).
. La formule composite a un ordre 1, comme précédemment. L'agrégation a fait baisser d'une puissance le terme en (a-b).Pour la méthode des trapèzes, la formule composite est
Le terme d'erreur s'écrit
![E(f)=-h^2 \frac{(b-a)}{12} f''(\eta),\quad \eta\in [a,b]](/pictures/frwiki/102/fa5cd8517e88267b0298c4f331c330d7.png) .
.La formule composite de Simpson prend la forme
et l'erreur devient
Autres méthodes de quadrature numérique
Méthode de calcul d'intégrale à plusieurs dimensions
Méthode de calcul d'intégrale de forme particulière
- Méthode de Laplace pour les intégrales du type
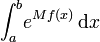 ;
; - Méthode du point col pour les intégrales du type
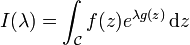 .
.
Voir aussi
- Intégrale
- Table d'intégrales
- Calcul intégral
- Calcul numérique d'une intégrale
- Primitive
- Règles de Bioche
- Portail des mathématiques
Catégories : Algorithme numérique | Intégration numérique
Wikimedia Foundation. 2010.

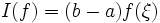
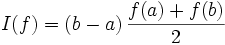
![E(f) = - \frac{(b-a)^3}{12} f''(\eta), \quad \eta \in [a,b]](/pictures/frwiki/48/0ec6fcc949089f29e2d21b5f2f752f35.png)
![I(f) = \frac{(b-a)}{6} \left[ f(a) + 4 f(m) + f(b) \right]](/pictures/frwiki/54/670a9d221d9e4d5450d144864868590a.png)
![E(f) = - \frac{(b-a)^5}{2880} f^{(4)}(\eta), \quad \eta \in [a,b]](/pictures/frwiki/54/6fa065e89b9fdefd0d09cf8ffb8b38ef.png)
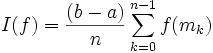
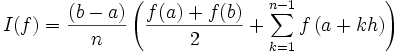
![I(f) = \frac{h}{6} \left[f(a)+f(b) + 2 \sum_{i=1}^{n-1} f(x_i) + 4 \sum_{i=0}^{n-1} f(x_i + h/2) \right]](/pictures/frwiki/99/cc29c034e0366e4e13b3e03461fbb21e.png)
![E(f) = -h^4 \frac{(b-a)}{2880} f^{(4)}(\eta),\quad \eta\in [a,b]](/pictures/frwiki/97/a0fa33f26aedac6eea6582c9d3782656.png)